
- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons

Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

7.4: Distributive Property
- Last updated
- Save as PDF
- Page ID 5035

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
- Simplify expressions using the distributive property
- Evaluate expressions using the distributive property
be prepared!
Before you get started, take this readiness quiz.
- Multiply: 3(0.25). If you missed this problem, review Example 5.3.5
- Simplify: 10 − (−2)(3). If you missed this problem, review Example 3.7.5 .
- Combine like terms: 9y + 17 + 3y − 2. If you missed this problem, review Example 2.3.10 .
Simplify Expressions Using the Distributive Property
Suppose three friends are going to the movies. They each need $9.25; that is, 9 dollars and 1 quarter. How much money do they need all together? You can think about the dollars separately from the quarters.

They need 3 times $9, so $27, and 3 times 1 quarter, so 75 cents. In total, they need $27.75. If you think about doing the math in this way, you are using the Distributive Property.
Definition: Distributive Property
If a, b, c are real numbers, then a(b + c) = ab + ac.
Back to our friends at the movies, we could show the math steps we take to find the total amount of money they need like this:
\[\begin{split} 3(9&.25) \\ 3(9 &+ 0.25) \\ 3(9) &+ 3(0.25) \\ 27 &+ 0.75 \\ 27&.75 \end{split}\]
In algebra, we use the Distributive Property to remove parentheses as we simplify expressions. For example, if we are asked to simplify the expression 3(x + 4), the order of operations says to work in the parentheses first. But we cannot add x and 4, since they are not like terms. So we use the Distributive Property, as shown in Example \(\PageIndex{1}\).
Example \(\PageIndex{1}\):
Simplify: 3(x + 4).
Exercise \(\PageIndex{1}\):
Simplify: 4(x + 2).
Exercise \(\PageIndex{2}\):
Simplify: 6(x + 7).
Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in Example 7.17 would look like this:
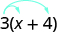
\[3 \cdot x + 3 \cdot 4\]
Example \(\PageIndex{2}\):
Simplify: 6(5y + 1).
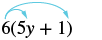
Exercise \(\PageIndex{3}\):
Simplify: 9(3y + 8).
Exercise \(\PageIndex{4}\):
Simplify: 5(5w + 9).
The distributive property can be used to simplify expressions that look slightly different from a(b + c). Here are two other forms.
If a, b, c are real numbers, then\[a(b + c) = ab + ac$$Other forms$$a(b − c) = ab − ac$$$$(b + c)a = ba + ca\]
Example \(\PageIndex{3}\):
Simplify: 2(x − 3).
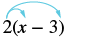
Exercise \(\PageIndex{5}\):
Simplify: 7(x − 6).
Exercise \(\PageIndex{6}\):
Simplify: 8(x − 5).
Do you remember how to multiply a fraction by a whole number? We’ll need to do that in the next two examples.
Example \(\PageIndex{4}\):
Simplify: \(\dfrac{3}{4}\)(n + 12).
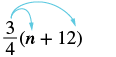
Exercise \(\PageIndex{7}\):
Simplify: \(\dfrac{2}{5}\)(p + 10).
\(\frac{2}{5}p + 4 \)
Exercise \(\PageIndex{8}\):
Simplify: \(\dfrac{3}{7}\)(u + 21).
\(\frac{3}{7}u +9 \)
Example \(\PageIndex{5}\):
Simplify: \(8 \left(\dfrac{3}{8}x + \dfrac{1}{4}\right)\).
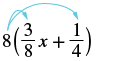
Exercise \(\PageIndex{9}\):
Simplify: \(6 \left(\dfrac{5}{6}y + \dfrac{1}{2}\right)\).
Exercise \(\PageIndex{10}\):
Simplify: \(12 \left(\dfrac{1}{3}n + \dfrac{3}{4}\right)\).
Using the Distributive Property as shown in the next example will be very useful when we solve money applications later.
Example \(\PageIndex{6}\):
Simplify: 100(0.3 + 0.25q).
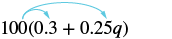
Exercise \(\PageIndex{11}\):
Simplify: 100(0.7 + 0.15p).
Exercise \(\PageIndex{12}\):
Simplify: 100(0.04 + 0.35d).
In the next example we’ll multiply by a variable. We’ll need to do this in a later chapter.
Example \(\PageIndex{7}\):
Simplify: \(m(n − 4)\).
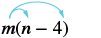
Notice that we wrote m • 4 as 4m. We can do this because of the Commutative Property of Multiplication. When a term is the product of a number and a variable, we write the number first.
Exercise \(\PageIndex{13}\):
Simplify: r(s − 2).
Exercise \(\PageIndex{14}\):
Simplify: y(z − 8).
The next example will use the ‘backwards’ form of the Distributive Property, (b + c)a = ba + ca.
Example \(\PageIndex{8}\):
Simplify: (x + 8)p.
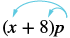
Exercise \(\PageIndex{15}\):
Simplify: (x + 2)p.
Exercise \(\PageIndex{16}\):
Simplify: (y + 4)q.
When you distribute a negative number, you need to be extra careful to get the signs correct.

Example \(\PageIndex{9}\):
Simplify: −2(4y + 1).
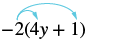
Exercise \(\PageIndex{17}\):
Simplify: −3(6m + 5).
Exercise \(\PageIndex{18}\):
Simplify: −6(8n + 11).
Example \(\PageIndex{10}\):
Simplify: −11(4 − 3a).
You could also write the result as 33a − 44. Do you know why?
Exercise \(\PageIndex{19}\):
Simplify: −5(2 − 3a).
Exercise \(\PageIndex{20}\):
Simplify: −7(8 − 15y).
In the next example, we will show how to use the Distributive Property to find the opposite of an expression. Remember, −a = −1 • a.
Example \(\PageIndex{11}\):
Simplify: −(y + 5).
Exercise \(\PageIndex{21}\):
Simplify: −(z − 11).
Exercise \(\PageIndex{22}\):
Simplify: −(x − 4).
Sometimes we need to use the Distributive Property as part of the order of operations. Start by looking at the parentheses. If the expression inside the parentheses cannot be simplified, the next step would be multiply using the distributive property, which removes the parentheses. The next two examples will illustrate this.
Example \(\PageIndex{12}\):
Simplify: 8 − 2(x + 3).
Exercise \(\PageIndex{23}\):
Simplify: 9 − 3(x + 2).
Exercise \(\PageIndex{24}\):
Simplify: 7x − 5(x + 4).
Example \(\PageIndex{13}\):
Simplify: 4(x − 8) − (x + 3).
Exercise \(\PageIndex{25}\):
Simplify: 6(x − 9) − (x + 12).
Exercise \(\PageIndex{26}\):
Simplify: 8(x − 1) − (x + 5).
Evaluate Expressions Using the Distributive Property
Some students need to be convinced that the Distributive Property always works. In the examples below, we will practice evaluating some of the expressions from previous examples; in part (a), we will evaluate the form with parentheses, and in part (b) we will evaluate the form we got after distributing. If we evaluate both expressions correctly, this will show that they are indeed equal.
Example \(\PageIndex{14}\):
When y = 10 evaluate: (a) 6(5y + 1) (b) 6 • 5y + 6 • 1.
(a) 6(5y + 1)
(b) 6 • 5y + 6 • 1
Notice, the answers are the same. When y = 10, 6(5y + 1) = 6 • 5y + 6 • 1. Try it yourself for a different value of y.
Exercise \(\PageIndex{27}\):
Evaluate when w = 3: (a) 5(5w + 9) (b) 5 • 5w + 5 • 9.
Exercise \(\PageIndex{28}\):
Evaluate when y = 2: (a) 9(3y + 8) (b) 9 • 3y + 9 • 8.
Example \(\PageIndex{15}\):
When y = 3, evaluate (a) −2(4y + 1) (b) −2 • 4y + (−2) • 1.
(a) −2(4y + 1)
(b) −2 • 4y + (−2) • 1
Exercise \(\PageIndex{29}\):
Evaluate when n = −2: (a) −6(8n + 11) (b) −6 • 8n + (−6) • 11.
Exercise \(\PageIndex{30}\):
Evaluate when m = −1: (a) −3(6m + 5) (b) −3 • 6m + (−3) • 5.
Example \(\PageIndex{16}\):
When y = 35 evaluate (a) −(y + 5) and (b) −y − 5 to show that −(y + 5) = −y − 5.
(a) −(y + 5)
(b) −y − 5
Exercise \(\PageIndex{31}\):
Evaluate when x = 36: (a) −(x − 4) (b) −x + 4 to show that −(x − 4) = − x + 4.
Exercise \(\PageIndex{32}\):
Evaluate when z = 55: (a) −(z − 10) (b) −z + 10 to show that −(z − 10) = − z + 10.
ACCESS ADDITIONAL ONLINE RESOURCES
Model Distribution
The Distributive Property
Practice Makes Perfect
In the following exercises, simplify using the distributive property.
- 6(c − 13)
- 7(y − 13)
- 7(3p − 8)
- 5(7u − 4)
- \(\dfrac{1}{2}\)(n + 8)
- \(\dfrac{1}{3}\)(u + 9)
- \(\dfrac{1}{4}\)(3q + 12)
- \(\dfrac{1}{5}\)(4m + 20)
- \(9 \left(\dfrac{5}{9} y − \dfrac{1}{3}\right)\)
- \(10 \left(\dfrac{3}{10} x − \dfrac{2}{5}\right)\)
- \(12 \left(\dfrac{1}{4} + \dfrac{2}{3} r\right)\)
- \(12 \left(\dfrac{1}{6} + \dfrac{3}{4} s\right)\)
- r(s − 18)
- u(v − 10)
- −2(y + 13)
- −3(a + 11)
- −7(4p + 1)
- −9(9a + 4)
- −3(x − 6)
- −4(q − 7)
- −9(3a − 7)
- −6(7x − 8)
- −(r + 7)
- −(q + 11)
- −(3x − 7)
- −(5p − 4)
- 5 + 9(n − 6)
- 12 + 8(u − 1)
- 16 − 3(y + 8)
- 18 − 4(x + 2)
- 4 − 11(3c − 2)
- 9 − 6(7n − 5)
- 22 − (a + 3)
- 8 − (r − 7)
- −12 − (u + 10)
- −4 − (c − 10)
- (5m − 3) − (m + 7)
- (4y − 1) − (y − 2)
- 5(2n + 9) + 12(n − 3)
- 9(5u + 8) + 2(u − 6)
- 9(8x − 3) − (−2)
- 4(6x − 1) − (−8)
- 14(c − 1) − 8(c − 6)
- 11(n − 7) − 5(n − 1)
- 6(7y + 8) − (30y − 15)
- 7(3n + 9) − (4n − 13)
In the following exercises, evaluate both expressions for the given value.
- 6 · 4v + 6 · 7
- 8 · 5u + 8 · 12
- \(3 \left(n + \dfrac{5}{6}\right)\)
- 3 • n + 3 • \(\dfrac{5}{6}\)
- 4 ⎛ ⎝ y + 3 8 ⎞ ⎠
- 4 • y + 4 • \(\dfrac{3}{8}\)
- −3(4y + 15)
- 3 • 4y + (−3) • 15
- −6(5p + 11)
- −6 • 5p + (−6) • 11
- −10(3m − 0.9)
- −10 • 3m − (−10)(0.9)
- −100(5n + 1.5)
- −100 • 5n + (−100)(1.5)
- −(y − 25)
- −y + 25
- −(w − 80)
- −w + 80
- −(p + 0.72)
- −p − 0.72
- −(q + 0.48)
- −q − 0.48
Everyday Math
- Use the distributive property to find the cost of 12 bottles bought individually at the convenience store. (Hint: notice that $1.99 is $2 − $0.01.)
- Is it a bargain to buy the iced tea at the grocery store by the case?
- Show how you can use the distributive property to find the cost of 3 bottles bought individually at the drug store.
- How much would Adele save by buying the 3-pack at the warehouse store?
Writing Exercises
- Simplify \(8 \left(x − \dfrac{1}{4}\right)\) using the distributive property and explain each step.
- Explain how you can multiply 4($5.97) without paper or a calculator by thinking of $5.97 as 6 − 0.03 and then using the distributive property.
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) What does this checklist tell you about your mastery of this section? What steps will you take to improve?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/[email protected] ."

IMAGES
VIDEO
COMMENTS
The main differences between community property are the in-community property states, there is an absolute 50-50 split of all property acquired during the marriage. In equitable distribution states, more assets may be considered "marital property," but the split is not necessarily 50-50. Identify five factors generally considered by courts dividing property inequitable property jurisdictions.
Sign in here. Dante Outten Eastern Gateway Community College Assignment 14.1 Property Division Review Answer the following questions: 1. Distinguish between separate and marital property. Give an example of each. 2. Describe the primary differences between community property and an equitable division approach to property division. 3.
Amanda Flores PLG215 Assignment 14.1: Property Division Review Due: 02/26/2023 1. Distinguish between separate and marital property. Give an example of each. Marital property includes any personal or real property acquired by either or both parties from the date of marriage until the date divorce papers are filed. Some examples of marital property are timeshares, lottery winnings, and club ...
The Distributive Property states that if a, b, c are real numbers, then a(b + c) = ab + ac. ... (0.25). If you missed this problem, review Example 5.3.5; Simplify: 10 − (−2)(3). If you missed this problem, review Example 3.7.5. Combine like terms: 9y + 17 + 3y − 2. ... 14(c − 1) − 8(c − 6) 11(n − 7) − 5(n − 1) 6(7y + 8) − ...
17 1 assignments and delegations flashcards unit 14 assignment 1 recap flashcards quizlet assignment 14 1 property division docx jessica nelson understanding assignments the writing center ... jessica nelson 5 13 20 family law professor maresa taylor assignment 14 1 property division review distinguish
Assignment 8.1 Review Questions. 50 terms. Michael-Tan13. Preview. Fordney's IHMO 9.1 Review Questions. 46 terms. ohwoahsusie. Preview. Kahoot Questions and Literary Lenses ... Insurance ch 14&15. 22 terms. Gibbyjock. Preview. Chapter 14 Tricare and Veterans health Care. 91 terms. lg0845788. Preview. Chapter 8 practice questions. 10 terms ...
the gaseous envelope of a planet. theory that Earth's rock layers formed in a global flood followed by the uplifting of rocks and mountain building over a short, violent period, possibly in the recent past. long-term weather patterns of a particular area. the state or process of rotting or decay.
ASSIGNMENT 14. In the following situation, identify each principal, agent, and act of agency. Also identify whether the agency is employment related. Cyrus hires Ben to work for him. Cyrus is an English professor who hates to grade papers. Ben is his nephew and an English major in college. Ben is paid $1 per page to grade student essay assignments.
11 remainder of 8. 748 divided by 3. 249 remainder of 1. The tank contains 896 gallons of water. The water must be shared equally among 112 persons. Each person should receive how many gallons of water? 8. Study with Quizlet and memorize flashcards containing terms like dividend, divisor, quotient and more.
Address Assignment Review Process Updated on 8/21/2023. Pg. 3 of 3 Address Assignment Email List 1. Postmaster USPS - [email protected], [email protected] 2. Deputy tax assessor - [email protected] 3. West Bay sanitary district - [email protected] 4. AT&T - (contact to be identified) 5.
Question: AssignmentStudent Name: Student ID:Question 1A division of a company has the following balances in its financial statements:Goodwill $900,000Plant $800,000Property. Assignment. Following a period of losses, the recoverable amount of the division is deemed to be $ 4 million. A recent valuation of the building showed that the ...
Answer Guide No. 1 Real Property and the Nature of Value. This Assignment is a Multiple Choice Assignment. Marks: 1 mark per question. Answer: 3 Option (3) is false. Value is not the key consideration in the analysis of highest and best use rather it is " that use which is most likely to produce the greatest return, in money of amenities ...
Correct Answer: 1 Option (1) is true, and therefore is the correct answer. An appeal from the Property Assessment Appeal Board to the British Columbia Supreme Court can only be made on a point of law, not of fact. Option (2) is false because an appeal of a Property Assessment Review Panel decision must first be made to the Property Assessment Appeal Board before appealing to the British ...
All vocabulary/ Q&A's for Unit 1/ Assignment 14. "Workbook Properties" Learn with flashcards, games, and more — for free. Fresh features from the #1 AI-enhanced learning platform.
If x =2 then x + 8 = 10. the addition property of equality. Select the property of equality used to arrive at the conclusion.If 1/3x = 5 then x = 15. the multiplication property of equality. Select the property of equality to arrive at the conclusion.If x - 3 = 7 then x = 10. the addition property of equality.
This assignment is a Multiple Choice Assignment. Marks: 1 mark per question. Answer: 3 Option (3) is the correct answer. Allocation is a technique in which a ratio of site value to property value is extracted from comparable sales in competitive locations and applied to the sale price of the subject property to develop the site value.
Match the following: "A." A cell body found in the spinal cord/Is always stimulatory. Match the following: "B." The system of motor neurons that innervates smooth and cardiac muscle and glands. Match the following: "C." A cell body of a parasympathetic postganglionic motor neuron/Fibers originate in the thoracic and lumbar regions of the spinal ...