trigonometry questions bbc bitesize

Trigonometry

The trigonomic ratios.

When it comes to trigonometry there are some key parts that we need to learn. There are many methods, here’s a couple that might help!

SOHCAHTOA - This acronym is used to help you remember the trigonometric ratios.

Sine of an angle =Opposite/Hypotenuse

Cosine of an angle = Adjacent/Hypotenuse

Tangent of an angle = Opposite/Adjacent

You need to remember these ratios in order to make sure you choose the right one to solve problems.

A few of my favourite ways to remember these are:

S__ome __O__ld __H__orses __C__an __A__lways __H__ear __T__heir __O__wners A__pproach

__S__ome __O__f __H__er __C__hildren __A__lways __H__ope __T__o __O__wn __A__pples

S__ome __O__ld __H__ippies __C__ome __A__lways __H__elping T__o __O__rder __A__nts

Use a song, use a mnemonic, use whatever you need but make sure you REMEMBER THESE ratios!

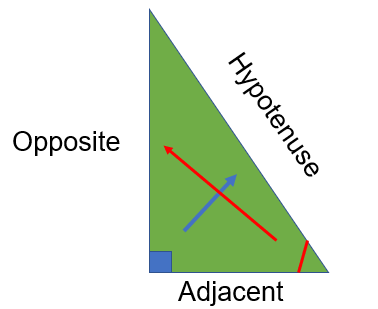
Labelling triangle recap

When we looked at Pythagoras we focused on identifying the Hypotenuse which is ALWAYS opposite the right angle. When we use trigonometry we will be either looking for an angle OR a side of a right angle triangle.

Therefore, in trigonometry we need to identify the other two triangles as well. These are the

Adjacent __and the Opposite.__

The Adjacent is adjacent to the angle whilst the Opposite is opposite the angle.

Here’s a diagram to show you what I mean:

Finding Angles

If you have two lengths of a right angle triangle using the trigonometric ratios you can work out the degree of the angles. Depending on the sides of the triangle you will use a different trigonometric ratio, however the process is similar for both of them:

Step 1: Label your triangle

• Step 2: Select your ratio
• Step 3: Divide the sides
• Step 4: Inverse the sine, cosine or tan function to find your angle (sin -1 or cos -1 or tan -1 )

Eg. Find the angle marked in this triangle:

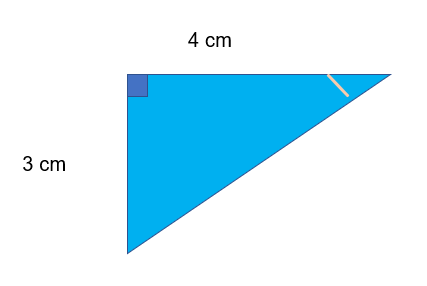
Step 2: Choose your ratio. If we look at our labelled triangle we can see that we have not got any information about the Hypotenuse, but we DO have information about the adjacent and opposite.

Therefore we want to choose a ratio that involves the Opposite and the Adjacent

SOH CAH TOA

In this case it must be the tan ratio

Tan of the angle =Opposite/Adjacent

Step 3: Tan of the angle =3/4

Step 4: Inverse the trigonometric function - on your calculator this will be a button that looks like tan-1

Inverse tan (3/4) = Tan-1 (3/4) = 36.869897645844 or 36.87 to 2 dp

It is REALLY important that you have your calculator in the correct setting. Make sure it is in the DEGREES setting or DEG.

Finding Lengths

To find the length of a trigonometric ratio we have a similar process:

• Step 1: Label the triangle
• Step 2: Select the ratio
• Step 3: Calculate
• Step 4: Check your answer!

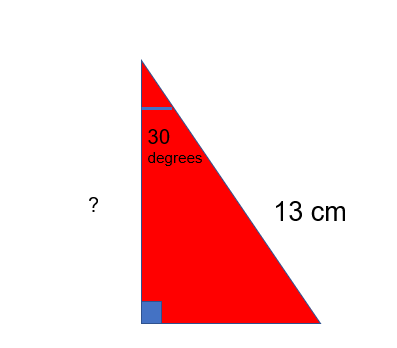
In this case the two values that we have or are looking for are the hypotenuse and the adjacent.

SOH C__AH__ TOA Therefore we will use the Cosine ratio

Cos of the angle =Adjacent/Hypotenuse

We can rearrange this equation to get:

Cos of the angle x Hypotenuse = Adjacent

(Cos (30)) x 13 = 11.26 (to 2 dp)

11.26 cm sounds right and would make a realistic triangle! (It it was 123542 I’d definitely double check!)

Take care to multiply Cos30 by 13 and not Cos (30 x 13) or you will get the incorrect value!

Trigonometry in real life

When it comes to the higher paper, you may often find questions that are wordy and require trigonometry.

For these questions make sure you sketch it out! Draw the description, create a triangle, label and solve.

Eg. Katie kicks a football towards a goal. The goal is 2.4 m from the ground and Katie is standing 3 metres away from the goal. If she wants to hit the bar what will be the angle of elevation?

Sketch out the problem

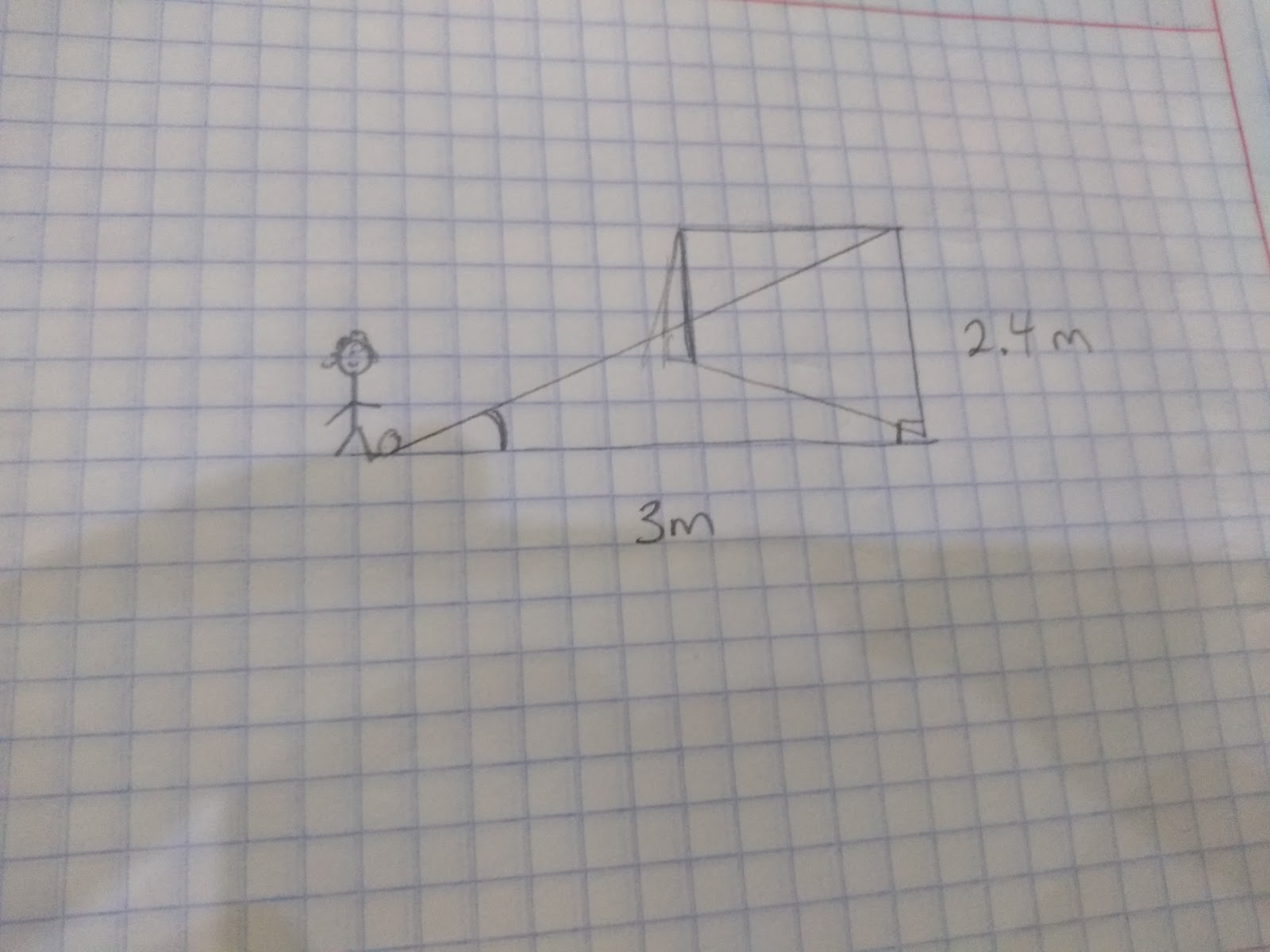
Label the sides, in this case we have information about the Opposite and the Adjacent side, therefore if we check SOH CAH TOA, we will want to find the inverse of the tangent of the angle

Tan Angle = Opposite/Adjacent

Angle = Tan -1 2.4/3 = 38.67 (to 2 dp)

Katie may want to miss the bar and score, in which case she will need to kick at an angle of just less than 38.67!!

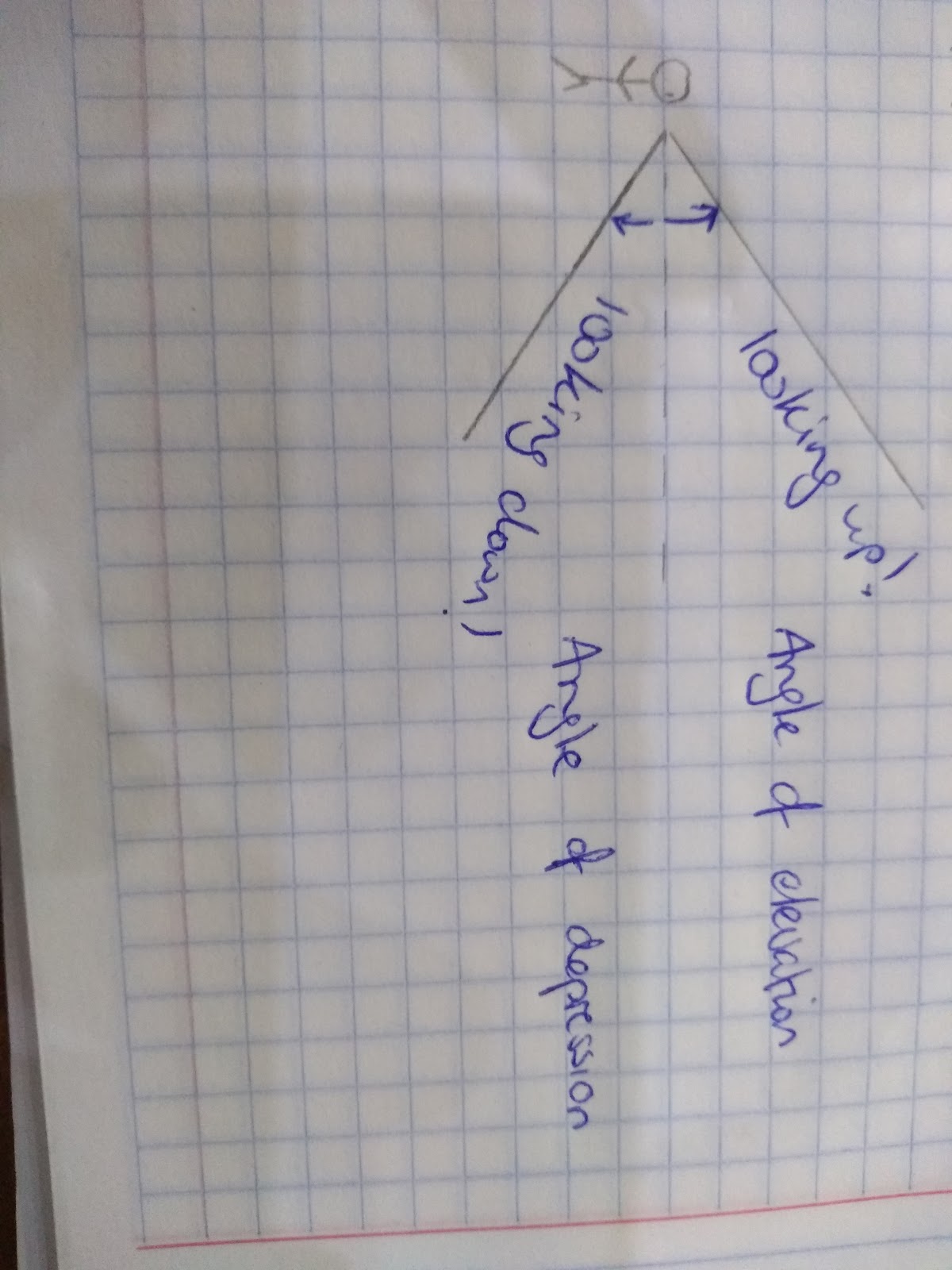
This question referred to an angle of elevation, that’s the angle that goes from the base upwards.

You may also be asked to find an angle of depression that goes from a high point downwards.

Trigonometry in 3D

We may also have to use trigonometry to solve problems involving 3D shapes.

For example:

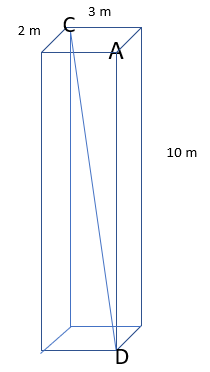
Find the angle CDA

Firstly we need to identify a right angle triangle connected to CD.

We can do this by creating a base from the diagonal of the rectangle on the bottom of the prism.

We then have the hypotenuse that is CD and the remaining side will be 10m.

To work out the base we can use Pythagoras!

Diagonal 2 = 2 2 + 3 2

Diagonal 2 = 4 + 9

Diagonal 2 = 13

Diagonal = Diagonal = √13 (I’m going to leave this as a surd to ensure my working is as accurate as possible)

Now we have two lengths we can use our trigonometric ratios to work out the angle. Once again sketch out the triangle to help you:

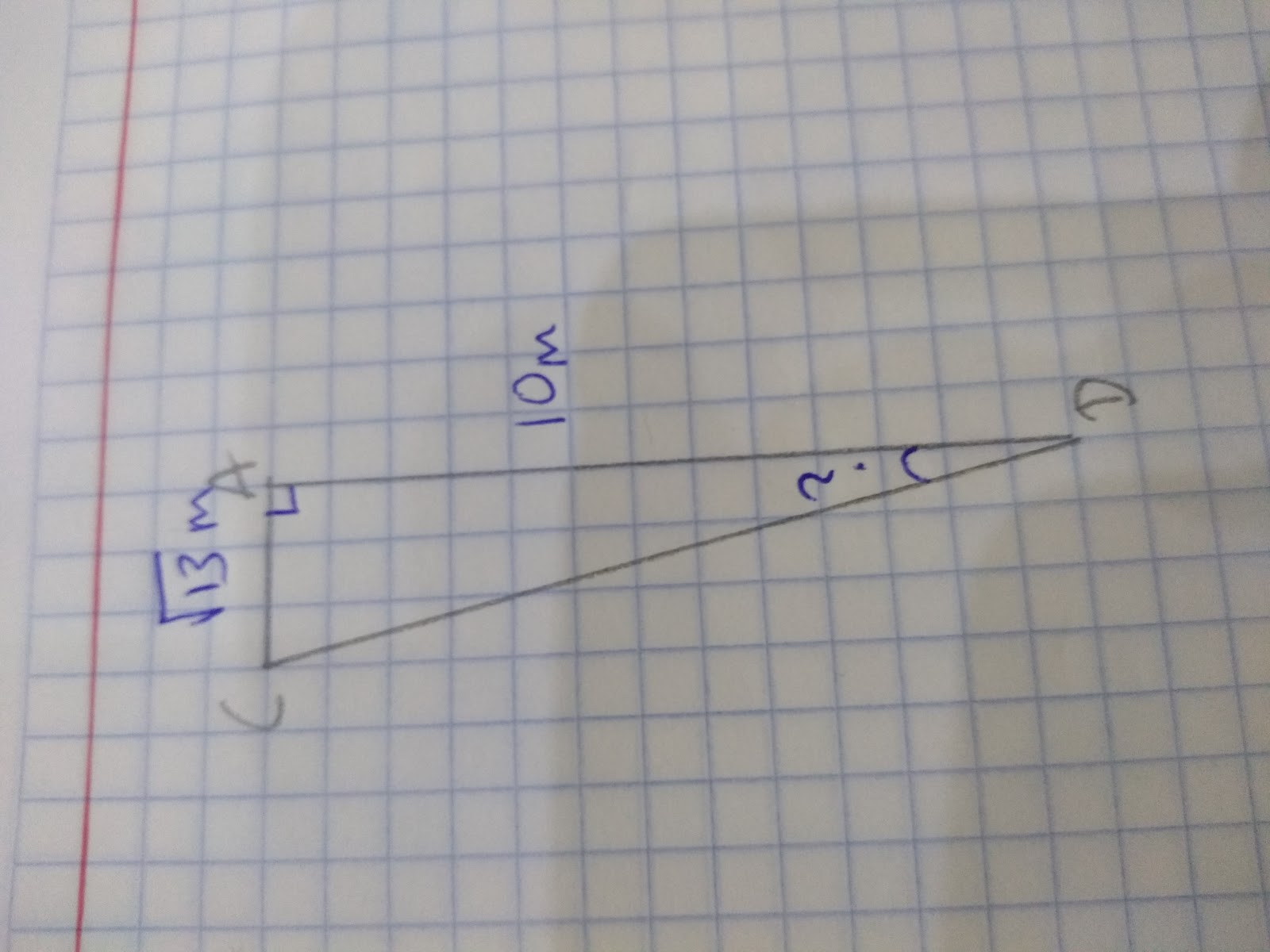
After labelling the triangles we should see that we have information about the opposite and the adjacent. Therefore we want to use the Tangent ratio.

Tan Angle = √13/10

Angle = Tan -1 √13/10 = 19.83 to 2 dp.

Key values to memorise

You will also be expected to memorise specific trigonometric ratios:

Learn this table!!! You technically can work these values out using Pythagoras however in the exam you won’t have time so LEARN THEM!!!

We can also use our trigonometric functions (sin, cos and tan) to work out the lengths and angles of triangles that don’t have right angles!!!

We can use the sine rule, which refers to the following angles and sides:

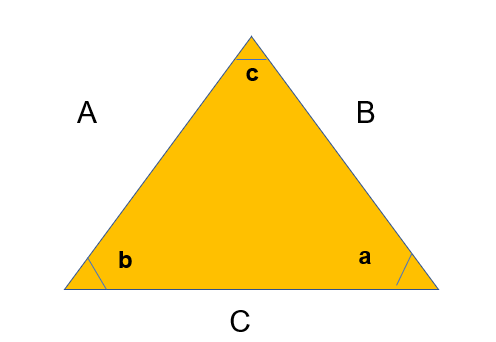
Sin a / A = Sin b / B = Sin c / C or A / Sin a = B / Sin b = C / Sin c

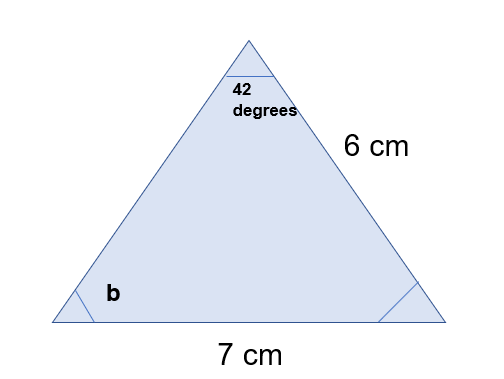
What is the angle b?

To work out be I can use the sine rule as I know:

Sin a / A = Sin b / B = Sin c / C

Sin b / 6 = Sin 42 / 7

To get sin b I just need to multiply by 6 and find the inverse of sine.

Sin b = sin 42 / 7 x 6

b= sin -1 (sin 42/7 x 6)

b = 35.00 (to 2 dp)

We can also use the other equation to work out lengths.

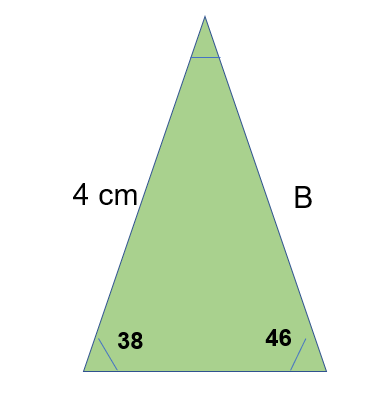
4 / Sin 38 = B / Sin 46

Therefore if we multiply both sides by sin 46 we’ll find B

4 /Sin 38 x Sin 46 = B

Cosine Rule

We can also use the cosine rule to find angles and sides.

To find angles:

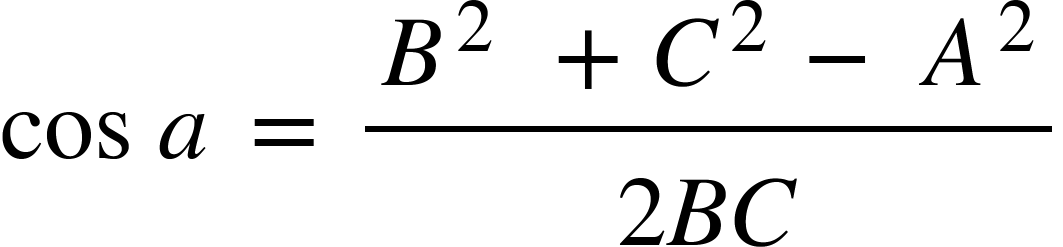
To find lengths:

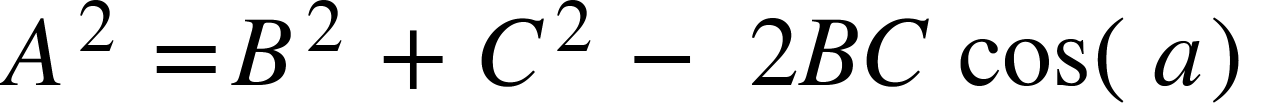
For example, calculate the missing length of this triangle:

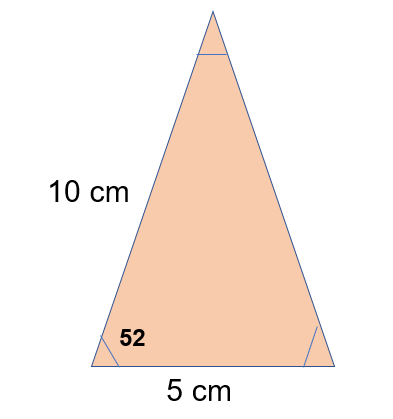
Think carefully about how the values given will fit the formula.

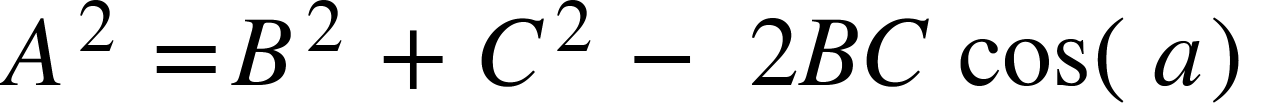
The ( a) stands for the missing angle, B and C are interchangable.

? 2 = 5 2 + 7 2 - 2(5)(7) cos(52)

? 2 = 25 +49 - 70cos52

? 2 = 30.9036…

We can also use the cosine rule to work out a missing length when given three sides:

Work out the angle of c:

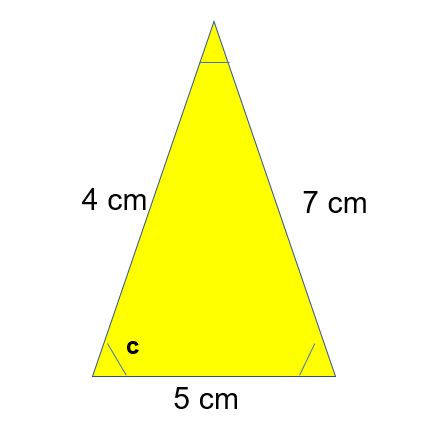
Once again, take care with your substitution! Cos c = Cos a in the formula!

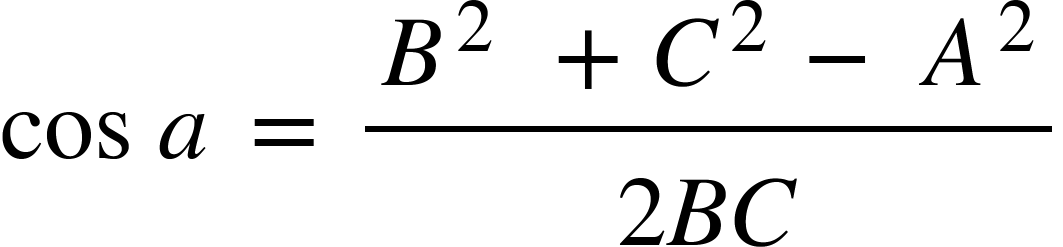
Finding the area using trigonomic ratios

We can also use trigonometric ratios to find the area of triangles!

Area of a triangle = 1/2 ABsin(c)

Remember this is you ever need to work out the area of a triangle but don’t have the height or base!

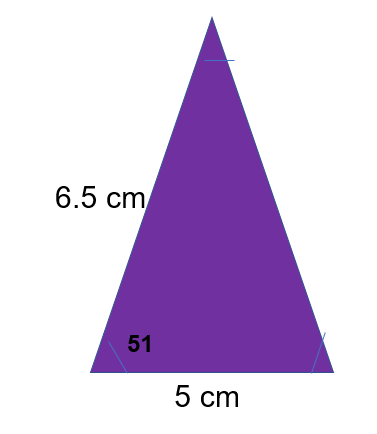
Area of a triangle = 1/2 ABsinc

When substituting in your values remember the little c is the angle that you’ve been given.

Area of a triangle= 1/2 (6.5)(5)sin(51) = 12.63 cm 2

Reset password New user? Sign up

Existing user? Log in

Bearing - Word Problems

Already have an account? Log in here.

• Andres Gonzalez
• Marco Faustini
• Mahindra Jain
• Kaustubh Miglani

Most bearing word problems involving trigonometry and angles can be reduced to finding relationships between angles and the measurements of the sides of a triangle . In this case, finding the right basic trigonometric functions to relate the angles and measurements are crucial for setting up and solving the problem correctly.

Trigonometry of angles and sides can be used on a daily basis in the workplace like in carpentry, construction work, engineering, etc.

Basic Definitions

Word problems, example problems.

Before jumping to the word problems, here are the basic definitions you need to be familiar with:

The angle of elevation of an object as seen by an observer is the angle between the horizontal and the line from the object to the observer's eye (also known as the line of sight ). The angle of elevation in the above diagram is \(\alpha^\circ\).

If the object is below the level of the observer, then the angle between the horizontal and the observer's line of sight is called the angle of depression . The angle of depression in the above diagram is \(\beta^\circ\).

If the height of a pole is \(2\sqrt3\) metres and the length of its shadow is \(2\) metres, then find the angle of elevation of the sun.

It is often useful to draw a diagram and remember how the basic trigonometric functions relate the angles and measurements of sides in a right triangle. Finding the right trigonometric function to relate the angles and measurements is crucial to solving the problems. We will demonstrate the principle of setting up and solving trigonometric word problems by working through several examples.

A surveyor in a helicopter at an elevation of 1000 meters measures the angle of depression to the far edge of an island as \( 24^\circ \) and the angle of depression to the near edge as \( 31^\circ \). How wide is the island, to the nearest meter? Let the horizontal distance between the helicopter and the island be \( d \), and the width of the island \( w \). Then \( \tan 24^\circ = \frac{1000}{d+w} \) and \( \tan 31^\circ = \frac{1000}{d} \), implying \( d = \frac{1000}{\tan 31^\circ} \). Substituting this into \( \tan 24^\circ = \frac{1000}{d+w} \) gives \[\begin{align} \tan 24^\circ &= \frac{1000}{\frac{1000}{\tan 31^\circ}+w} \\ \tan 24^\circ \left(\frac{1000}{\tan 31^\circ}+w \right) &= 1000 \\ w &= \frac{1000\left( 1 - \frac{\tan 24^\circ}{ \tan 31^\circ }\right)}{\tan 24^\circ} \\\\ & \approx 581.75 . \end{align}\] Thus, the width of the island is 582 meters Alternatively, you can calculate the difference between \(\cot 24^\circ\) and \(\cot 31^\circ\) (which is 0.581757292) and multiply it by 1000 meters. \(_\square\)

Andrew was flying a kite on a hill, but he dumped his kite into the pond below. If the length of the string of his kite is 150 meters and the angle of depression from his position to the kite is \(30^\circ\), then how high is the hill where he is standing? Let's first draw a diagram for a better understanding of the problem: So it is a right triangle with base angle \(30^\circ\), hypotenuse 150 meters, and the side \(h\) opposite to the given angle being the same as the height of the hill. We use the sine ratio to find the height: \[\begin{align} \sin 30^\circ&=\dfrac{h}{150} \\ \dfrac 12 &=\dfrac{h}{150} \\ \\ \Rightarrow h&=75 \text{ (m)}. \end{align}\] Hence the hill is 75 meters above the lake. \(_\square\)

The angle of elevation of the top of an incomplete vertical pillar at a horizontal distance of 100 meters from its base is 45 degrees. If the angle of elevation of the top of the complete pillar from the same spot is to be 60 degrees, then by how much the height of the incomplete pillar should be increased? Let's draw a diagram to figure out the situation: Let \(BC\) be the height of the incomplete pillar, and \(BD\) the height of the complete pillar. We are given that \(BC=100\text{ m}, \angle BAC = 45^\circ,\) and \(\angle BAD = 60^\circ\). And we assume that the length of \(CD\) is \(x\) meters. In triangle \( ABC\), we know that \[\begin{align} \tan 45^\circ & =\frac{BC}{AB} \\\\ AB & =BC \\ & =100 \text{ m}.\end{align}\] Similarly, in triangle \(ABD\), we know that \[\begin{align} \tan 60^\circ & =\frac{BD}{AB} \\ \sqrt 3 & = \frac{BD}{100} \\\\ \Rightarrow BD & =100 \sqrt 3 \text{ m}.\end{align}\] And from the above figure, \[\begin{align} BD&=BC+CD \\ 100\sqrt3 &=100+x \\\\ \Rightarrow x&=100 \big( \sqrt3 -1 \big) \text{ m}. \end{align}\] Hence the height of the incomplete pillar is to be increased by \(100 \big( \sqrt3 -1 \big) \text{ m} \) to complete the pillar. \(_\square\)

Jim and Ted live on one side of the river, and Martha lives on the other side. The distance across the river is 100 yards. Ted, who lives downstream from Matha, measures an angle of 35 degrees between the shoreline and a straight line leading to Martha's house. Jim, who lives upstream from Martha, measures an angle of 60 degrees. How far apart do Ted and Jim live? First off, a picture will help (to get your "bearing"--no pun intended). The relative positions of Martha, Jim, and Ted are represented in this picture: Now, it is much easier to visualize what is going on. The distance in yards from Jim to the position directly across the stream from Matha is given as \[\tan 60^\circ = \frac{100}{x}.\] And the distance in yards from Jim to the position directly across the stream from Matha is given as \[\tan 35^\circ = \frac{100}{y}.\] So, the distance from Ted to Jim is given by \[\begin{align} \text{Distance} &= x + y \\ &= \frac{100}{\tan 60^\circ} + \frac{100}{\tan 35^\circ}\\\\ &= 57.7 + 142.8 \\ &= 200.5 \text{ (yards)}.\ _\square \end{align}\]

A private plane flies for 1.3 hours at 110 mph on a bearing of 40°. Then it turns and continues another 1.5 hours at the same speed, but on a bearing of 130°. At the end of this time, how far is the plane from its starting point? The bearings tell us the angles from "due north" in a clockwise direction. Since 130 – 40 = 90, the two bearings give us a right triangle. From the times and rates, we have \[\begin{align} 1.3 × 110 &= 143\\ 1.5 × 110 &= 165. \end{align}\] Now, let's give the geometrical shape to our problem and set up a triangle: Using the Pythagorean theorem , we get \[\begin{align} m^2 & =143^2 + 165^2 \\ & =20449 + 27225 \\ & =47674 \\\\ \Rightarrow m & = 218.34. \end{align} \] Hence the plane is approximately 218 miles away at the end of the time. \(_\square\)

Try the following bearing word problems:

A pole of 8-feet height is located on top of a house, right on the edge of the ceiling. From a point on the ground, the angle of elevation to the top of the house is \(17^\circ\) and the angle of elevation to the top of the pole is \(21.8^\circ.\)

Find the height of the house.

A tower stands at the center of a circular park. \(A\) and \(B\) are two points on the boundary of the park such that \(AB\) subtends an angle of \( 60^\circ\) at the foot of the tower and the angle of elevation of the top of the tower from \(A\) or \(B\) is \( 30^\circ.\)

Find the height of the tower.

This section is meant to enhance the problem-solving skills of bearing word problems. Here an example is illustrated followed by some problems for you to attempt:

A six-meter-long ladder leans against a building. If the ladder makes an angle of \(60^\circ\) with the ground, (1) how far up the wall does the ladder reach, and (2) how far from the wall is the base of the ladder? To understand the situation, let's draw a diagram: (1) From the above diagram, we get the following equation to obtain the value of \(h:\) \[\begin{align} \sin 60^\circ & =\dfrac h6 \\ \Rightarrow h & =6 \times \sin 60^\circ \\ & =3 \sqrt 3. \end{align} \] So the ladder can reach \(3\sqrt3 \) meters up the wall. \[\] (2) Similarly, we can get the value of \(b\) as follows: \[\begin{align} \cos 60^\circ &=\dfrac b6 \\ \Rightarrow b&=6 \times \cos 60^\circ \\ &=3. \end{align}\] Hence the base of the ladder is 3 meters from the wall. \(_\square\)

Here are the problems to gain a strong grab over the bearing concept:

The angle of elevation of a cloud from a point \(h\) meters above a lake is \(\theta\). The angle of depression of its reflection in the lake is \(45^{\circ}\). Find the height of the cloud in meters.

Linda measures the angle of elevation from a point on the ground to the top of a tree and finds it to be 35 degrees. She then walks 20 meters towards the tree and finds the angle of elevation from this new point to the top of the tree to be 45 degrees. Find the height of the tree (in meters).

Give your answer to three significant figures.

From the top of a 7-meter-high building, the angle of elevation of the top of a cable tower is \(60°\) and the angle of depression of its foot is \(45°.\) Determine the height of the tower in meters.

If the angles of elevation of the top of a tower from three collinear points \(A, B,\) and \(C\), on a line leading to the foot of the tower, are \(30^{\circ},45^{\circ},\) and \(60^{\circ},\) respectively, then the ratio \(AB:BC\) is \(\text{__________}.\)

Lengths in Right Triangles

Trigonometric Equations

Problem Loading...

Note Loading...

Set Loading...

• S1 to S3 Maths
• National 4 Maths
• National 4 Apps
• National 5 Maths
• National 5 Apps
• Higher Maths
• Higher Apps
• Find a Maths Tutor
• Buy Maths Books
• About Maths.scot

Course content

• Understand how sin, cos and tan are defined for angles from 0° to 360°
• Understand period and related angles
• Solve basic trigonometric equations.

Textbook page references

• TeeJay Maths Book N5 pp.196-203
• Zeta National 5+ Maths pp.214-216
• Leckie National 5 Maths pp.272-280

Related angles

The trig functions sin, cos and tan can be defined for angles greater than 90° by thinking about this diagram:

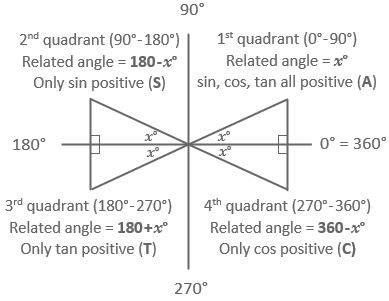
The four quadrants contain congruent right-angled triangles with the angle \(x^\circ\) at the centre.

The actual angle is measured anticlockwise from the 0° line .

• 1st quadrant: The actual angle is \(x^\circ.\)
• 2nd quadrant: The actual angle is half a turn and then back \(x^\circ.\) So that's 180–\(x^\circ.\)
• 3rd quadrant: The actual angle is half a turn and then another \(x^\circ\). So that's 180+\(x^\circ.\)
• 4th quadrant: The actual angle is a full turn and then back \(x^\circ.\) So that's 360–\(x^\circ.\)

These four angles are what we call related .

Example 1:   \(x\) = 30°

• sin 30° = \(1 \over 2\)
• sin (180–30)° = sin 150° = \(1 \over 2\)
• sin (180+30)° = sin 210° = \(-\frac{1}{2}\)
• sin (360–30)° = sin 330° = \(-\frac{1}{2}\)

Apart from the negatives, they're all equal. That's because these four angles are related.

Example 2:   \(x\) = 45°

• cos 45° = \(\frac{\sqrt{2}}{2}\)
• cos (180–45)° = cos 135° = \(-\frac{\sqrt{2}}{2}\)
• cos (180+45)° = cos 225° = \(-\frac{\sqrt{2}}{2}\)
• cos (360–45)° = cos 315° = \(\frac{\sqrt{2}}{2}\)

Again, these are related angles, so they're equal apart from the negatives.

Example 3:   \(x\) = 60°

• tan 60° = \(\sqrt{3}\)
• tan (180–60)° = tan 120° = \(-\sqrt{3}\)
• tan (180+60)° = tan 240° = \(\sqrt{3}\)
• tan (360–60)° = tan 300° = \(-\sqrt{3}\)

Same again: they're equal apart from the negatives, because they are related angles.

ASTC diagram

This is also called a CAST diagram, but we prefer ASTC as it keeps the letters in the correct quadrant order.

• All Sinners Take Care.
• All Students Take Calculus.
• Add Sugar To Coffee.
• A Smart Trig Class.
• All Stations To Central.

Here is a simpler version of the diagram:

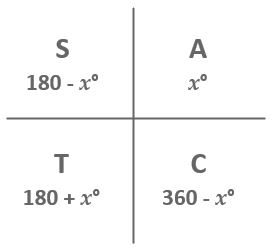
If you want to understand why some of the values for related angles are positive and some are negative, that's easy. Just go back to your study of the basic trig graphs and take a look at when they are above or below the \(x\)-axis. Above is positive and below is negative – simple!

Trig equations

Trig equations have an infinity of solutions because the wave-like graphs of these functions repeat endlessly.

For this reason, Nat 5 exams ask for such equations to be solved within a given domain , often \(0 \leq x \lt 360.\)

When solving any trig equation, we recommend always finding the related acute angle . This means the 1st quadrant (0° to 90°) angle that is related to the solutions.

We will use the Greek letter alpha (\(\alpha\)) for the related acute angle.

Once we know the related acute angle, we will use it to find the solutions.

Find a Maths tutor

Example 1 (calculator)

Solve the equation \( cos\ x^\circ=0.5 \), for \(0 \leq x \lt 360.\)

The related acute angle, \( \alpha\ = cos^{-1}\ 0.5=60^\circ \)

Because \(cos\ x\) > 0, there are solutions in the 1 st (A) and 4 th (C) quadrants.

So \(x=\alpha\)  or  \(x=360-\alpha\)

\(x=60^\circ\)  or  \(x=360-60=300^\circ\)

Example 2 (calculator)

Solve the equation \( cos\ x^\circ=-0.5 \), for \(0 \leq x \lt 360.\)

The only difference here is the negative.

The related acute angle is the same: \( \alpha\ = cos^{-1}\ 0.5=60^\circ \)

Because \(cos\ x\) < 0, there are solutions in the 2 nd (S) and 3 rd (T) quadrants.

So \(x=180-\alpha\)  or  \(x=180+\alpha\)

\(x=180-60=120^\circ\)  or  \(x=180+60=240^\circ\)

Example 3 (calculator)

Solve the equation \( sin\ x^\circ=-0.4 \), for \(0 \leq x \lt 360.\)

The related acute angle \( \alpha\ = sin^{-1}\ 0.4 = 23.6^\circ \) (to 1 d.p.)

Because \(sin\ x\) < 0, there are solutions in the 3 rd (T) and 4 th (C) quadrants.

So \(x=180+\alpha\)  or  \(x=360-\alpha\)

\(x=180+23.6=203.6^\circ\)  or  \(x=360-23.6=336.4^\circ\) (to 1 d.p.)

Recommended student books

Example 4 (calculator)

Solve the equation \( tan\ x^\circ=5 \), for \(0 \leq x \lt 360.\)

The related acute angle \( \alpha\ = tan^{-1}\ 5 = 78.7^\circ \) (to 1 d.p.)

Because \(tan\ x\) > 0, there are solutions in the 1 st (A) and 3 rd (T) quadrants.

So \(x=\alpha\)  or  \(x=180+\alpha\)

\(x=78.7^\circ\)  or  \(x=180+78.7=258.7^\circ\) (to 1 d.p.)

Example 5 (calculator)

Solve the equation \( 9\tiny\ \normalsize tan\ x^\circ-1=6 \), for \(0 \leq x \lt 360.\)

The previous examples were easier than exam level. This is more like it!

First we rearrange to find a value for \(tan\ x\):

\( 9\tiny\ \normalsize tan\ x^\circ-1=6 \) \( 9\tiny\ \normalsize tan\ x^\circ=7 \) \( tan\ x^\circ=\large \frac{7}{9} \normalsize \)

The related acute angle \( \alpha\ = tan^{-1}\ \large \frac{7}{9} \normalsize = 37.9^\circ \) (to 1 d.p.)

\(x=37.9^\circ\)  or  \(x=180+37.9=217.9^\circ\) (to 1 d.p.)

Example 6 (calculator)

Solve the equation \( 3\tiny\ \normalsize sin\ x^\circ+5=4 \), for \(0 \leq x \lt 360.\)

Rearrange to make \(sin\ x\) the subject:

\( 3\tiny\ \normalsize sin\ x^\circ+5=4 \) \( 3\tiny\ \normalsize sin\ x^\circ=-1 \) \( sin\ x^\circ=-\large \frac{1}{3} \normalsize \)

The related acute angle \( \alpha\ = sin^{-1}\ \large \frac{1}{3} \normalsize = 19.5^\circ \) (to 1 d.p.)

\(x=180+19.5=199.5^\circ\)  or  \(x=360-19.5=340.5^\circ\) (to 1 d.p.)

Recommended revision guides

Example 7 (non-calculator).

Write the following in order of size, starting with the smallest.

\(sin\ 200^\circ\)   \(sin\ 160^\circ\)   \(sin\ 180^\circ\)

Justify your answer.

Obviously this isn't an equation, but a question very like it appeared as Q9 on 2015 Paper 1 .

Answering it without a calculator requires either sketching the graph of \(y=sin\ x\) or thinking about the ASTC diagram.

• \(200^\circ\) is in the 3 rd (T) quadrant, so \(sin\ 200^\circ \lt 0\)
• \(160^\circ\) is in the 2 nd (S) quadrant, so \(sin\ 160^\circ \gt 0\)
• \(180^\circ\) is between the 2 nd and 3 rd quadrants, so \(sin\ 180^\circ=0\)

In order:  \(sin\ 200^\circ\)  \(sin\ 180^\circ\)  \(sin\ 160^\circ\)

Example 8 (calculator)

SQA National 5 Maths 2014 P2 Q12

Solve the equation \( 11\tiny\ \normalsize cos\ x^\circ-2=3 \), for \(0 \leq x \leq 360.\)

\( 11\tiny\ \normalsize cos\ x^\circ-2=3 \) \( 11\tiny\ \normalsize cos\ x^\circ=5 \) \( cos\ x^\circ=\large \frac{5}{11} \normalsize \)

The related acute angle \( \alpha\ = cos^{-1}\ \large \frac{5}{11} \normalsize = 63.0^\circ \) (to 1 d.p.)

\(x=63.0^\circ\)  or  \(x=360-63.0=297.0^\circ\) (to 1 d.p.)

Example 9 (calculator)

SQA National 5 Maths 2016 P2 Q14

Solve the equation \( 2\tiny\ \normalsize tan\ x^\circ+5=-4 \), for \(0 \leq x \leq 360.\)

\( 2\tiny\ \normalsize tan\ x^\circ+5=-4 \) \( 2\tiny\ \normalsize tan\ x^\circ=-9 \) \( tan\ x^\circ=-\large \frac{9}{2} \normalsize \)

The related acute angle \( \alpha\ = tan^{-1}\ \large \frac{9}{2} \normalsize = 77.5^\circ \) (to 1 d.p.)

Because \(tan\ x\) < 0, there are solutions in the 2 nd (S) and 4 th (C) quadrants.

So \(x=180-\alpha\)  or  \(x=360-\alpha\)

\(x=180-77.5=102.5^\circ\)  or  \(x=360-77.5=282.5^\circ\) (to 1 d.p.)

N5 Maths practice papers

Example 10 (calculator).

SQA National 5 Maths 2018 P2 Q8

Solve the equation \( 7\tiny\ \normalsize sin\ x^\circ+2=3 \), for \(0 \leq x \lt 360.\)

\( 7\tiny\ \normalsize sin\ x^\circ+2=3 \) \( 7\tiny\ \normalsize sin\ x^\circ=1 \) \( sin\ x^\circ=\large \frac{1}{7} \normalsize \)

The related acute angle \( \alpha\ = sin^{-1}\ \large \frac{1}{7} \normalsize = 8.2^\circ \) (to 1 d.p.)

Because \(sin\ x\) > 0, there are solutions in the 1 st (A) and 2 nd (S) quadrants.

So \(x=\alpha\)  or  \(x=180-\alpha\)

\(x=8.2^\circ\)  or  \(x=180-8.2=171.8^\circ\) (to 1 d.p.)

Example 11 (calculator)

SQA National 5 Maths 2019 P2 Q14

Solve the equation \( 5\tiny\ \normalsize cos\ x^\circ+2=1 \), for \(0 \leq x \leq 360.\)

\( 5\tiny\ \normalsize cos\ x^\circ+2=1 \) \( 5\tiny\ \normalsize cos\ x^\circ=-1 \) \( cos\ x^\circ=-\large \frac{1}{5} \normalsize \)

The related acute angle \( \alpha\ = cos^{-1}\ \large \frac{1}{5} \normalsize = 78.5^\circ \) (to 1 d.p.)

\(x=180-78.5=101.5^\circ\)  or  \(x=180+78.5=258.5^\circ\) (to 1 d.p.)

Example 12 (calculator)

SQA National 5 Maths 2022 P2 Q9

Solve the equation \( 3\tiny\ \normalsize sin\ x^\circ+4=6 \), for \(0 \leq x \leq 360.\)

\( 3\tiny\ \normalsize sin\ x^\circ+4=6 \) \( 3\tiny\ \normalsize sin\ x^\circ=2 \) \( sin\ x^\circ=\large \frac{2}{3} \normalsize \)

The related acute angle \( \alpha\ = sin^{-1}\ \large \frac{2}{3} \normalsize = 41.8^\circ \) (to 1 d.p.)

\(x=41.8^\circ\)  or  \(x=180-41.8=138.2^\circ\) (to 1 d.p.)

Example 13 (calculator)

SQA National 5 Maths 2024 P2 Q11

Solve the equation \( 17\tiny\ \normalsize sin\ x^\circ+1=9 \), for \(0 \leq x \lt 360.\)

\( 17\tiny\ \normalsize sin\ x^\circ+1=9 \) \( 17\tiny\ \normalsize sin\ x^\circ=8 \) \( sin\ x^\circ=\large \frac{8}{17} \normalsize \)

The related acute angle \( \alpha\ = sin^{-1}\ \large \frac{8}{17} \normalsize = 28.1^\circ \) (to 1 d.p.)

\(x=28.1^\circ\)  or  \(x=180-28.1=151.9^\circ\) (to 1 d.p.)

Need a Nat 5 Maths tutor?

Just use this handy little widget and our partner Bark.com will help you find one.

Maths.scot worksheet

Past paper questions, other great resources.

Click here to study the trig equations notes on National5.com.

You may also want to check out their Nat 5 Maths  self-study course . We think it's excellent. If you decide to enrol, just use coupon code " Maths.scot " to get £10 discount.

To use this resource a subscription to Go Teach Maths is required. A subscription gives you access to every resource on the website!

Individual Subscription

School subscription.

• Comprehensive topic coverage
• Over 7000 classroom resources
• GCSE & IGCSE coverage

A subscription to Go Teach Maths gives you access to every resource on the website!

Log in to your individual or school account

Or subscribe from only £25 per year!

Reset your password

Please enter the registered email address for your individual or school subscription.

Trigonometry Without a Calculator

Presentations.

Demonstration

Answer Maze

Teacher-Led Activities

Exam Questions

AQA Foundation

Edexcel Higher

2-Minute Feedback Form

[email protected]

• About Go Teach Maths
• What Do Teachers Say About GTM?
• Terms & Conditions

© Go Teach Maths

Privacy Overview

3D Trigonometry Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

BBC Bitesize - Exam Revision 4+

Flashcards, quizzes and guides, bbc media applications technologies limited.

• #54 in Education
• 4.5 • 3.8K Ratings

Screenshots

Description.

Free flashcards, quizzes and more on the BBC Bitesize - Exam Revision app. Get ready for the GCSEs, TGAU, Nationals and Highers with maths, science, english, history and geography revision resources, plus many other subjects across England, Northern Ireland, Scotland and Wales. The Bitesize app is suitable for students in years 10+/S4+, who are 14-16 years old. BBC Bitesize is used by over 1.5 million students per week. For more educational materials, including content for younger learners, visit the BBC Bitesize website at https://www.bbc.co.uk/bitesize KEY FEATURES - Bitesize flashcards summarise the key points of a topic using bullet points and labelled diagrams. Quiz flashcards help you to practise with multiple-choice questions. Video and audio flashcards feature lots of visual recaps and audio clips. - Revision guides explain key concepts to help you recap topics across all of your subjects. Most guides contain a ‘test’ section with multiple-choice quizzes. There are also sample exam questions for subjects like biology, chemistry, physics, English literature and English language. - Sign in with your free BBC account to set your subjects and exam board. It’s easy to save flashcards and revision guides for quick reference as you revise. - Available on iPhone and iPad. - The BBC Bitesize - Exam Revision app is completely free and there are no in-app purchases. RELIABLE AND TRUSTWORTHY All BBC Bitesize revision guides, flashcards and quizzes are created by curriculum experts and designed to be exam board-specific. Our content is written by curriculum authors and checked by educational consultants to ensure it follows the National Curriculum and the appropriate exam boards. SIGN IN AND CHOOSE YOUR SUBJECTS: EXAM BOARDS: - England: AQA, Edexcel, Eduqas, OCR - Northern Ireland: CCEA - Wales: WJEC - Scotland: SQA LEVELS: - GCSE - TGAU - Welsh Baccalaureate (WBQ) - Highers - National 5 - National 4 - Àrd Ìre - Nàiseanta 5 - Nàiseanta 4 --- To give you the best experience, this app tracks your selected nation, language, subjects and exam specifications to provide you with customised revision content. The app uses technologies similar to performance cookies. The BBC uses these for internal purposes to analyse and improve the app and its content. You can choose to opt out of this from the in-app settings menu. We've made some important changes to our Privacy and Cookies Policy and we want you to know what this means for you and your data. Find out more at https://www.bbc.co.uk/usingthebbc/your-data-matters. Find out about your privacy rights and the BBC’s Privacy and Cookies Policy at https://www.bbc.co.uk/privacy.

Version 4.5.6

We've been making improvements and fixing bugs.

Ratings and Reviews

3.8K Ratings

Utterly Brilliant…

I don’t normally leave reviews but this app is absolutely incredible provided you use it in the correct way; as a knowledge maintainer and perhaps booster. Learn your stuff (hopefully from your teacher but often) from the Bitesize website and use the app as a booster and together they make a wonderful learning aid, especially for people with busy lives who are often short of time. A more in depth quiz with questions a little more challenging (I.e. not multiple choice) would be nice in conjunction with the current quizzes, but there’s always room for improvement and all in all a great app.

Developer Response ,

Hi Louis, Thank you so much for this amazing feedback - it makes us happy to know you're such a massive fan of the app! We're always looking at ways to improve so we will definitely look into how we can make the quizzes a bit more challenging and varied - it's been on our list for a while! Thanks again! The Bitesize App Team

More detail

A Year 10 student here from a top grammar school ( not to brag hehe ). The only problem I have with the app is that there just isn’t enough detail when compared to the website itself. I downloaded the app to get a more enjoyable experience with a polished interface that couldn’t be created on a website, however I came to an unpleasant surprise when the lack of notes were there. I get it about the whole condense important stuff, but... especially for subjects like RS/RE you really need to pack in the points and drench them in quotes. Also, I don’t know if my school just does this, but we have a ‘themes’ paper, and that whole subject isn’t even on there. So... you know. My main issue is the detail, maybe just import all the info from the website to the app, people only download the app for the interface, that shouldn’t be a reason to cut down on imports quotes... and also add more questions in the quiz.

Hello, Thank you for your feedback. We are keen to keep improving our Bitesize app and its accessibility in order to make the content as useful as it can be, and user feedback helps us to achieve this. I will certainly hand your suggestion across to the development team who can take your comments into consideration when discussing future developments of the app. Unfortunately, I cannot put a timescale on this, but I hope that in the meantime you continue to use and enjoy our educational resources. Kind regards, Lizzie

Good app but can be glitchy

The app is good due to it having most of the subjects however I don’t seem to find a GCSE sociology section while looking Wales or English GCSE subjects in the app but is on the website . This isn’t as big of a deal but I do need it for some help on the go before I do tests and such . The app itself is good and is quite detailed however my loading screen glitches out a lot and I had to refill out my exam board and my subjects then it just does it again . I’ve re-downloaded it many times and it sometimes doesn’t work but it sometimes does . Depends weather it likes me that day or not lol . Anyway , good app for revision since there is quite a lot of detail in both flash cards and the whole textbooks type-esk and I’ll recommend it

Hi there! Thanks for your review. We’re sorry to hear that you’ve been experiencing glitches when using our app on your iPhone. We've found and fixed an issue at our end which we think caused this. Can we invite you to try again and let us know what happens? If you could also send us details of your device and version of iOS that would be incredibly helpful. Thanks. The Bitesize App Team

App Privacy

The developer, BBC Media Applications Technologies Limited , indicated that the app’s privacy practices may include handling of data as described below. For more information, see the developer’s privacy policy .

Data Linked to You

The following data may be collected and linked to your identity:

• Contact Info
• Identifiers

Data Not Linked to You

The following data may be collected but it is not linked to your identity:

• Diagnostics

Privacy practices may vary based on, for example, the features you use or your age. Learn More

Information

English, Gaelic, Irish, Welsh

• Developer Website
• App Support
• Privacy Policy

More By This Developer

BBC iPlayer

BBC News - UK & World Stories

BBC Weather

BBC Sport - News & Live Scores

CBeebies Playtime Island

You Might Also Like

My Past Papers

Adapt - Revision & Assessment

My English Literature GCSE

Exam Countdown - School & Uni

RevisePal - GCSE Exam Revision