deforestation research paper pdf

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 06 May 2020

Deforestation and world population sustainability: a quantitative analysis

• Mauro Bologna 1   na1 &
• Gerardo Aquino 2 , 3 , 4   na1  

Scientific Reports volume  10 , Article number:  7631 ( 2020 ) Cite this article

192k Accesses

53 Citations

1443 Altmetric

Metrics details

• Applied mathematics
• Environmental impact
• Population dynamics
• Statistical physics, thermodynamics and nonlinear dynamics

In this paper we afford a quantitative analysis of the sustainability of current world population growth in relation to the parallel deforestation process adopting a statistical point of view. We consider a simplified model based on a stochastic growth process driven by a continuous time random walk, which depicts the technological evolution of human kind, in conjunction with a deterministic generalised logistic model for humans-forest interaction and we evaluate the probability of avoiding the self-destruction of our civilisation. Based on the current resource consumption rates and best estimate of technological rate growth our study shows that we have very low probability, less than 10% in most optimistic estimate, to survive without facing a catastrophic collapse.

Similar content being viewed by others

Deforestation reduces rainfall and agricultural revenues in the Brazilian Amazon

Deforestation in Colombian protected areas increased during post-conflict periods

Historical dynamics of landslide risk from population and forest-cover changes in the Kivu Rift

Introduction.

In the last few decades, the debate on climate change has assumed global importance with consequences on national and global policies. Many factors due to human activity are considered as possible responsible of the observed changes: among these water and air contamination (mostly greenhouse effect) and deforestation are the mostly cited. While the extent of human contribution to the greenhouse effect and temperature changes is still a matter of discussion, the deforestation is an undeniable fact. Indeed before the development of human civilisations, our planet was covered by 60 million square kilometres of forest 1 . As a result of deforestation, less than 40 million square kilometres currently remain 2 . In this paper, we focus on the consequence of indiscriminate deforestation.

Trees’ services to our planet range from carbon storage, oxygen production to soil conservation and water cycle regulation. They support natural and human food systems and provide homes for countless species, including us, through building materials. Trees and forests are our best atmosphere cleaners and, due to the key role they play in the terrestrial ecosystem, it is highly unlikely to imagine the survival of many species, including ours, on Earth without them. In this sense, the debate on climate change will be almost obsolete in case of a global deforestation of the planet. Starting from this almost obvious observation, we investigate the problem of the survival of humanity from a statistical point of view. We model the interaction between forests and humans based on a deterministic logistic-like dynamics, while we assume a stochastic model for the technological development of the human civilisation. The former model has already been applied in similar contexts 3 , 4 while the latter is based on data and model of global energy consumption 5 , 6 used as a proxy for the technological development of a society. This gives solidity to our discussion and we show that, keeping the current rate of deforestation, statistically the probability to survive without facing a catastrophic collapse, is very low. We connect such probability to survive to the capability of humankind to spread and exploit the resources of the full solar system. According to Kardashev scale 7 , 8 , which measures a civilisation’s level of technological advancement based on the amount of energy they are able to use, in order to spread through the solar system we need to be able to harness the energy radiated by the Sun at a rate of ≈4 × 10 26 Watt. Our current energy consumption rate is estimated in ≈10 13 Watt 9 . As showed in the subsections “Statistical Model of technological development” and “Numerical results” of the following section, a successful outcome has a well defined threshold and we conclude that the probability of avoiding a catastrophic collapse is very low, less than 10% in the most optimistic estimate.

Model and Results

Deforestation.

The deforestation of the planet is a fact 2 . Between 2000 and 2012, 2.3 million Km 2 of forests around the world were cut down 10 which amounts to 2 × 10 5 Km 2 per year. At this rate all the forests would disappear approximatively in 100–200 years. Clearly it is unrealistic to imagine that the human society would start to be affected by the deforestation only when the last tree would be cut down. The progressive degradation of the environment due to deforestation would heavily affect human society and consequently the human collapse would start much earlier.

Curiously enough, the current situation of our planet has a lot in common with the deforestation of Easter Island as described in 3 . We therefore use the model introduced in that reference to roughly describe the humans-forest interaction. Admittedly, we are not aiming here for an exact exhaustive model. It is probably impossible to build such a model. What we propose and illustrate in the following sections, is a simplified model which nonetheless allows us to extrapolate the time scales of the processes involved: i.e. the deterministic process describing human population and resource (forest) consumption and the stochastic process defining the economic and technological growth of societies. Adopting the model in 3 (see also 11 ) we have for the humans-forest dynamics

where N represent the world population and R the Earth surface covered by forest. β is a positive constant related to the carrying capacity of the planet for human population, r is the growth rate for humans (estimated as r  ~ 0.01 years −1 ) 12 , a 0 may be identified as the technological parameter measuring the rate at which humans can extract the resources from the environment, as a consequence of their reached technological level. r ’ is the renewability parameter representing the capability of the resources to regenerate, (estimated as r ’ ~ 0.001 years −1 ) 13 , R c the resources carrying capacity that in our case may be identified with the initial 60 million square kilometres of forest. A closer look at this simplified model and at the analogy with Easter Island on which is based, shows nonetheless, strong similarities with our current situation. Like the old inhabitants of Easter Island we too, at least for few more decades, cannot leave the planet. The consumption of the natural resources, in particular the forests, is in competition with our technological level. Higher technological level leads to growing population and higher forest consumption (larger a 0 ) but also to a more effective use of resources. With higher technological level we can in principle develop technical solutions to avoid/prevent the ecological collapse of our planet or, as last chance, to rebuild a civilisation in the extraterrestrial space (see section on the Fermi paradox). The dynamics of our model for humans-forest interaction in Eqs. ( 1 , 2 ), is typically characterised by a growing human population until a maximum is reached after which a rapid disastrous collapse in population occurs before eventually reaching a low population steady state or total extinction. We will use this maximum as a reference for reaching a disastrous condition. We call this point in time the “no-return point” because if the deforestation rate is not changed before this time the human population will not be able to sustain itself and a disastrous collapse or even extinction will occur. As a first approximation 3 , since the capability of the resources to regenerate, r ′, is an order of magnitude smaller than the growing rate for humans, r , we may neglect the first term in the right hand-side of Eq. ( 2 ). Therefore, working in a regime of the exploitation of the resources governed essentially by the deforestation, from Eq. ( 2 ) we can derive the rate of tree extinction as

The actual population of the Earth is N  ~ 7.5 × 10 9 inhabitants with a maximum carrying capacity estimated 14 of N c  ~ 10 10 inhabitants. The forest carrying capacity may be taken as 1 R c  ~ 6 × 10 7 Km 2 while the actual surface of forest is \(R\lesssim 4\times {10}^{7}\) Km 2 . Assuming that β is constant, we may estimate this parameter evaluating the equality N c ( t ) =  βR ( t ) at the time when the forests were intact. Here N c ( t ) is the instantaneous human carrying capacity given by Eq. ( 1 ). We obtain β  ~  N c / R c  ~ 170.

In alternative we may evaluate β using actual data of the population growth 15 and inserting it in Eq. ( 1 ). In this case we obtain a range \(700\lesssim \beta \lesssim 900\) that gives a slightly favourable scenario for the human kind (see below and Fig.  4 ). We stress anyway that this second scenario depends on many factors not least the fact that the period examined in 15 is relatively short. On the contrary β  ~ 170 is based on the accepted value for the maximum human carrying capacity. With respect to the value of parameter a 0 , adopting the data relative to years 2000–2012 of ref. 10 ,we have

The time evolution of system ( 1 ) and ( 2 ) is plotted in Figs.  1 and 2 . We note that in Fig.  1 the numerical value of the maximum of the function N ( t ) is N M  ~ 10 10 estimated as the carrying capacity for the Earth population 14 . Again we have to stress that it is unrealistic to think that the decline of the population in a situation of strong environmental degradation would be a non-chaotic and well-ordered decline, that is also way we take the maximum in population and the time at which occurs as the point of reference for the occurrence of an irreversible catastrophic collapse, namely a ‘no-return’ point.

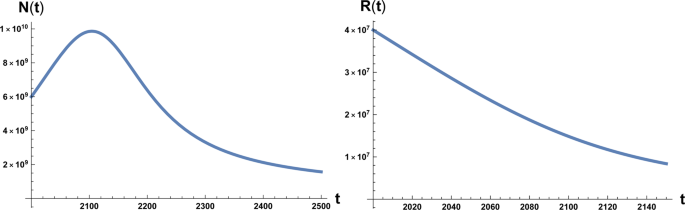
On the left: plot of the solution of Eq. ( 1 ) with the initial condition N 0  = 6 × 10 9 at initial time t  = 2000 A.C. On the right: plot of the solution of Eq. ( 2 ) with the initial condition R 0  = 4 × 10 7 . Here β  = 700 and a 0  = 10 −12 .

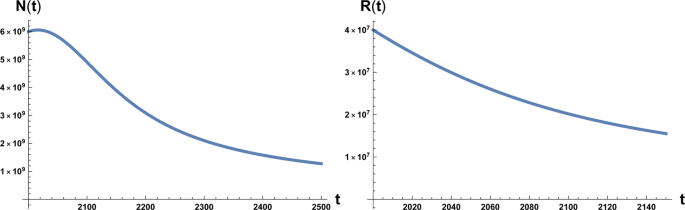
On the left: plot of the solution of Eq. ( 1 ) with the initial condition N 0  = 6 × 10 9 at initial time t  = 2000 A.C. On the right: plot of the solution of Eq. ( 2 ) with the initial condition R 0  = 4 × 10 7 . Here β  = 170 and a 0  = 10 −12 .

Statistical model of technological development

According to Kardashev scale 7 , 8 , in order to be able to spread through the solar system, a civilisation must be capable to build a Dyson sphere 16 , i.e. a maximal technological exploitation of most the energy from its local star, which in the case of the Earth with the Sun would correspond to an energy consumption of E D  ≈ 4 × 10 26 Watts, we call this value Dyson limit. Our actual energy consumption is estimated in E c  ≈ 10 13 Watts (Statistical Review of World Energy source) 9 . To describe our technological evolution, we may roughly schematise the development as a dichotomous random process

where T is the level of technological development of human civilisation that we can also identify with the energy consumption. α is a constant parameter describing the technological growth rate (i.e. of T ) and ξ ( t ) a random variable with values 0, 1. We consider therefore, based on data of global energy consumption 5 , 6 an exponential growth with fluctuations mainly reflecting changes in global economy. We therefore consider a modulated exponential growth process where the fluctuations in the growth rate are captured by the variable ξ ( t ). This variable switches between values 0, 1 with waiting times between switches distributed with density ψ ( t ). When ξ ( t ) = 0 the growth stops and resumes when ξ switches to ξ ( t ) = 1. If we consider T more strictly as describing the technological development, ξ ( t ) reflects the fact that investments in research can have interruptions as a consequence of alternation of periods of economic growth and crisis. With the following transformation,

differentiating both sides respect to t and using Eq. ( 5 ), we obtain for the transformed variable W

where \(\bar{\xi }(t)=2[\xi (t)-\langle \xi \rangle ]\) and 〈ξ 〉 is the average of ξ ( t ) so that \(\bar{\xi }(t)\) takes the values ±1.

The above equation has been intensively studied, and a general solution for the probability distribution P ( W , t ) generated by a generic waiting time distribution can be found in literature 17 . Knowing the distribution we may evaluate the first passage time distribution in reaching the necessary level of technology to e.g. live in the extraterrestrial space or develop any other way to sustain population of the planet. This characteristic time has to be compared with the time that it will take to reach the no-return point. Knowing the first passage time distribution 18 we will be able to evaluate the probability to survive for our civilisation.

If the dichotomous process is a Poissonian process with rate γ then the correlation function is an exponential, i.e.

and Eq. ( 7 ) generates for the probability density the well known telegrapher’s equation

We note that the approach that we are following is based on the assumption that at random times, exponentially distributed with rate γ , the dichotomous variable \(\bar{\xi }\) changes its value. With this assumption the solution to Eq. ( 9 ) is

where I n ( z ) are the modified Bessel function of the first kind. Transforming back to the variable T we have

where for sake of compactness we set

In Laplace transform we have

The first passage time distribution, in laplace transform, is evaluated as 19

Inverting the Laplace transform we obtain

which is confirmed (see Fig.  3 ) by numerical simulations. The time average to get the point x for the first time is given by

which interestingly is double the time it would take if a pure exponential growth occurred, depends on the ratio between final and initial value of T and is independent of γ . We also stress that this result depends on parameters directly related to the stage of development of the considered civilisation, namely the starting value T 1 , that we assume to be the energy consumption E c of the fully industrialised stage of the civilisation evolution and the final value T , that we assume to be the Dyson limit E D , and the technological growth rate α . For the latter we may, rather optimistically, choose the value α  = 0.345, following the Moore Law 20 (see next section). Using the data above, relative to our planet’s scenario, we obtain the estimate of 〈 t 〉 ≈ 180 years. From Figs.  1 and 2 we see that the estimate for the no-return time are 130 and 22 years for β  = 700 and β  = 170 respectively, with the latter being the most realistic value. In either case, these estimates based on average values, being less than 180 years, already portend not a favourable outcome for avoiding a catastrophic collapse. Nonetheless, in order to estimate the actual probability for avoiding collapse we cannot rely on average values, but we need to evaluate the single trajectories, and count the ones that manage to reach the Dyson limit before the ‘no-return point’. We implement this numerically as explained in the following.

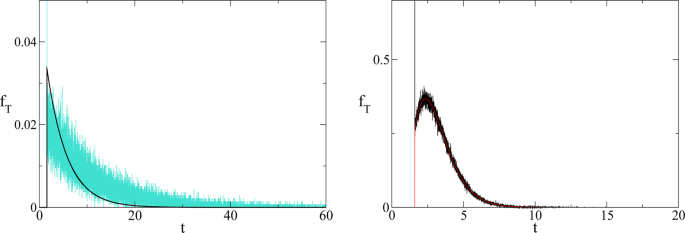
(Left) Comparison between theoretical prediction of Eq. ( 15 ) (black curve) and numerical simulation of Eq. ( 3 ) (cyan curve) for γ  = 4 (arbitrary units). (Right) Comparison between theoretical prediction of Eq. ( 15 ) (red curve) and numerical simulation of Eq. ( 3 ) (black curve) for γ  = 1/4 (arbitrary units).

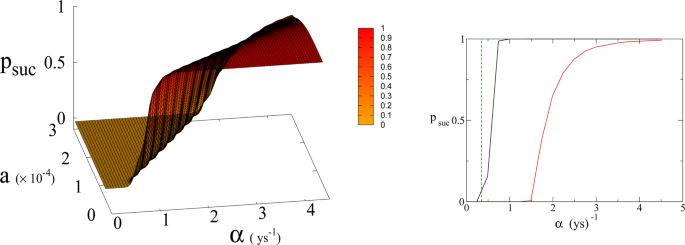
(Left panel) Probability p suc of reaching Dyson value before reaching “no-return” point as function of α and a for β  = 170. Parameter a is expressed in Km 2 ys −1 . (Right panel) 2D plot of p suc for a  = 1.5 × 10 −4 Km 2 ys −1 as a function of α . Red line is p suc for β  = 170. Black continuous lines (indistinguishable) are p suc for β  = 300 and 700 respectively (see also Fig.  6 ). Green dashed line indicates the value of α corresponding to Moore’s law.

Numerical results

We run simulations of Eqs. ( 1 ), ( 2 ) and ( 5 ) simultaneously for different values of of parameters a 0 and α for fixed β and we count the number of trajectories that reach Dyson limit before the population level reaches the “no-return point” after which rapid collapse occurs. More precisely, the evolution of T is stochastic due to the dichotomous random process ξ ( t ), so we generate the T ( t ) trajectories and at the same time we follow the evolution of the population and forest density dictated by the dynamics of Eqs. ( 1 ), ( 2 ) 3 until the latter dynamics reaches the no-return point (maximum in population followed by collapse). When this happens, if the trajectory in T ( t ) has reached the Dyson limit we count it as a success, otherwise as failure. This way we determine the probabilities and relative mean times in Figs.  5 , 6 and 7 . Adopting a weak sustainability point of view our model does not specify the technological mechanism by which the successful trajectories are able to find an alternative to forests and avoid collapse, we leave this undefined and link it exclusively and probabilistically to the attainment of the Dyson limit. It is important to notice that we link the technological growth process described by Eq. ( 5 ) to the economic growth and therefore we consider, for both economic and technological growth, a random sequence of growth and stagnation cycles, with mean periods of about 1 and 4 years in accordance with estimates for the driving world economy, i.e. the United States according to the National Bureau of Economic Research 21 .

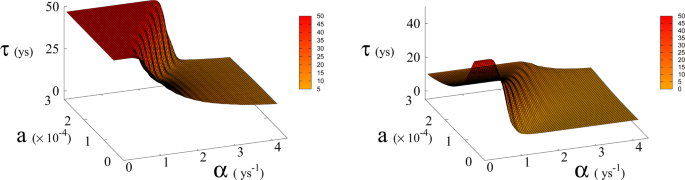
Average time τ (in years) to reach Dyson value before hitting “no-return” point (success, left) and without meeting Dyson value (failure, right) as function of α and a for β  = 170. Plateau region (left panel) where τ  ≥ 50 corresponds to diverging τ , i.e. Dyson value not being reached before hitting “no-return” point and therefore failure. Plateau region at τ  = 0 (right panel), corresponds to failure not occurring, i.e. success. Parameter a is expressed in Km 2 ys −1 .

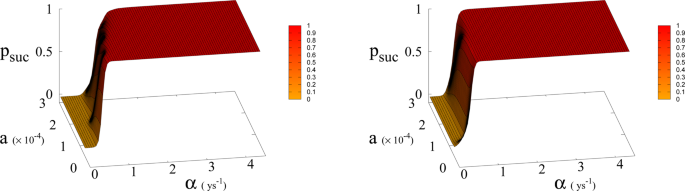
Probability p suc of reaching Dyson value before hitting “no-return” point as function of α and a for β  = 300 (left) and 700 (right). Parameter a is expressed in Km 2 ys −1 .

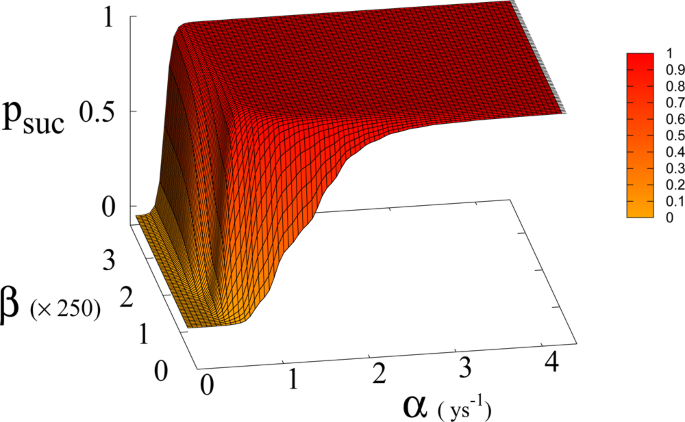
Probability of reaching Dyson value p suc before reaching “no-return” point as function of β and α for a  = 1.5 × 10 −4 Km 2 ys −1 .

In Eq. ( 1 , 2 ) we redefine the variables as N ′ =  N / R W and R ′ =  R / R W with \({R}_{W}\simeq 150\times {10}^{6}\,K{m}^{2}\) the total continental area, and replace parameter a 0 accordingly with a  =  a 0  ×  R W  = 1.5 × 10 −4 Km 2 ys −1 . We run simulations accordingly starting from values \({R{\prime} }_{0}\) and \({N{\prime} }_{0}\) , based respectively on the current forest surface and human population. We take values of a from 10 −5 to 3 × 10 −4 Km 2 ys −1 and for α from 0.01 ys −1 to 4.4 ys −1 . Results are shown in Figs.  4 and 6 . Figure  4 shows a threshold value for the parameter α , the technological growth rate, above which there is a non-zero probability of success. This threshold value increases with the value of the other parameter a . As shown in Fig.  7 this values depends as well on the value of β and higher values of β correspond to a more favourable scenario where the transition to a non-zero probability of success occurs for smaller α , i.e. for smaller, more accessible values, of technological growth rate. More specifically, left panel of Fig.  4 shows that, for the more realistic value β  = 170, a region of parameter values with non-zero probability of avoiding collapse corresponds to values of α larger than 0.5. Even assuming that the technological growth rate be comparable to the value α  = log(2)/2 = 0.345 ys −1 , given by the Moore Law (corresponding to a doubling in size every two years), therefore, it is unlikely in this regime to avoid reaching the the catastrophic ‘no-return point’. When the realistic value of a  = 1.5 × 10 4 Km 2 ys −1 estimated from Eq. ( 4 ), is adopted, in fact, a probability less than 10% is obtained for avoiding collapse with a Moore growth rate, even when adopting the more optimistic scenario corresponding to β  = 700 (black curve in right panel of Fig.  4 ). While an α larger than 1.5 is needed to have a non-zero probability of avoiding collapse when β  = 170 (red curve, same panel). As far as time scales are concerned, right panel of Fig.  5 shows for β  = 170 that even in the range α  > 0.5, corresponding to a non-zero probability of avoiding collapse, collapse is still possible, and when this occurs, the average time to the ‘no-return point’ ranges from 20 to 40 years. Left panel in same figure, shows for the same parameters, that in order to avoid catastrophe, our society has to reach the Dyson’s limit in the same average amount of time of 20–40 years.

In Fig.  7 we show the dependence of the model on the parameter β for a  = 1.5 × 10 −4 .

We run simulations of Eqs. ( 1 ), ( 2 ) and ( 5 ) simultaneously for different values of of parameters a 0 and α depending on β as explained in Methods and Results to generate Figs.  5 , 6 and 7 . Equations ( 1 ), ( 2 ) are integrated via standard Euler method. Eq. ( 5 ) is integrated as well via standard Euler method between the random changes of the variable ξ . The stochastic dichotomous process ξ is generated numerically in the following way: using the random number generator from gsl library we generate the times intervals between the changes of the dichotomous variable ξ  = 0, 1, with an exponential distribution(with mean values of 1 and 4 years respectively), we therefore obtain a time series of 0 and 1 for each trajectory. We then integrate Eq. ( 5 ) in time using this time series and we average over N  = 10000 trajectories. The latter procedure is used to carry out simulations in Figs.  3 and 4 as well in order to evaluate the first passage time probabilities. All simulations are implemented in C++.

Fermi paradox

In this section we briefly discuss a few considerations about the so called Fermi paradox that can be drawn from our model. We may in fact relate the Fermi paradox to the problem of resource consumption and self destruction of a civilisation. The origin of Fermi paradox dates back to a casual conversation about extraterrestrial life that Enrico Fermi had with E. Konopinski, E. Teller and H. York in 1950, during which Fermi asked the famous question: “where is everybody?”, since then become eponymous for the paradox. Starting from the closely related Drake equation 22 , 23 , used to estimate the number of extraterrestrial civilisations in the Milky Way, the debate around this topic has been particularly intense in the past (for a more comprehensive covering we refer to Hart 24 , Freitas 25 and reference therein). Hart’s conclusion is that there are no other advanced or ‘technological’ civilisations in our galaxy as also supported recently by 26 based on a careful reexamination of Drake’s equation. In other words the terrestrial civilisation should be the only one living in the Milk Way. Such conclusions are still debated, but many of Hart’s arguments are undoubtedly still valid while some of them need to be rediscussed or updated. For example, there is also the possibility that avoiding communication might actually be an ‘intelligent’ choice and a possible explanation of the paradox. On several public occasions, in fact, Professor Stephen Hawking suggested human kind should be very cautious about making contact with extraterrestrial life. More precisely when questioned about planet Gliese 832c’s potential for alien life he once said: “One day, we might receive a signal from a planet like this, but we should be wary of answering back”. Human history has in fact been punctuated by clashes between different civilisations and cultures which should serve as caveat. From the relatively soft replacement between Neanderthals and Homo Sapiens (Kolodny 27 ) up to the violent confrontation between native Americans and Europeans, the historical examples of clashes and extinctions of cultures and civilisations have been quite numerous. Looking at human history Hawking’s suggestion appears as a wise warning and we cannot role out the possibility that extraterrestrial societies are following similar advice coming from their best minds.

With the help of new technologies capable of observing extrasolar planetary systems, searching and contacting alien life is becoming a concrete possibility (see for example Grimaldi 28 for a study on the chance of detecting extraterrestrial intelligence), therefore a discussion on the probability of this occurring is an important opportunity to assess also our current situation as a civilisation. Among Hart’s arguments, the self-destruction hypothesis especially needs to be rediscussed at a deeper level. Self-destruction following environmental degradation is becoming more and more an alarming possibility. While violent events, such as global war or natural catastrophic events, are of immediate concern to everyone, a relatively slow consumption of the planetary resources may be not perceived as strongly as a mortal danger for the human civilisation. Modern societies are in fact driven by Economy, and, without giving here a well detailed definition of “economical society”, we may agree that such a kind of society privileges the interest of its components with less or no concern for the whole ecosystem that hosts them (for more details see 29 for a review on Ecological Economics and its criticisms to mainstream Economics). Clear examples of the consequences of this type of societies are the international agreements about Climate Change. The Paris climate agreement 30 , 31 is in fact, just the last example of a weak agreement due to its strong subordination to the economic interests of the single individual countries. In contraposition to this type of society we may have to redefine a different model of society, a “cultural society”, that in some way privileges the interest of the ecosystem above the individual interest of its components, but eventually in accordance with the overall communal interest. This consideration suggests a statistical explanation of Fermi paradox: even if intelligent life forms were very common (in agreement with the mediocrity principle in one of its version 32 : “there is nothing special about the solar system and the planet Earth”) only very few civilisations would be able to reach a sufficient technological level so as to spread in their own solar system before collapsing due to resource consumption.

We are aware that several objections can be raised against this argument and we discuss below the one that we believe to be the most important. The main objection is that we do not know anything about extraterrestrial life. Consequently, we do not know the role that a hypothetical intelligence plays in the ecosystem of the planet. For example not necessarily the planet needs trees (or the equivalent of trees) for its ecosystem. Furthermore the intelligent form of life could be itself the analogous of our trees, so avoiding the problem of the “deforestation” (or its analogous). But if we assume that we are not an exception (mediocrity principle) then independently of the structure of the alien ecosystem, the intelligent life form would exploit every kind of resources, from rocks to organic resources (animal/vegetal/etc), evolving towards a critical situation. Even if we are at the beginning of the extrasolar planetology, we have strong indications that Earth-like planets have the volume magnitude of the order of our planet. In other words, the resources that alien civilisations have at their disposal are, as order of magnitude, the same for all of them, including ourselves. Furthermore the mean time to reach the Dyson limit as derived in Eq.  6 depends only on the ratio between final and initial value of T and therefore would be independent of the size of the planet, if we assume as a proxy for T energy consumption (which scales with the size of the planet), producing a rather general result which can be extended to other civilisations. Along this line of thinking, if we are an exception in the Universe we have a high probability to collapse or become extinct, while if we assume the mediocrity principle we are led to conclude that very few civilisations are able to reach a sufficient technological level so as to spread in their own solar system before the consumption of their planet’s resources triggers a catastrophic population collapse. The mediocrity principle has been questioned (see for example Kukla 33 for a critical discussion about it) but on the other hand the idea that the humankind is in some way “special” in the universe has historically been challenged several times. Starting with the idea of the Earth at the centre of the universe (geocentrism), then of the solar system as centre of the universe (Heliocentrism) and finally our galaxy as centre of the universe. All these beliefs have been denied by the facts. Our discussion, being focused on the resource consumption, shows that whether we assume the mediocrity principle or our “uniqueness” as an intelligent species in the universe, the conclusion does not change. Giving a very broad meaning to the concept of cultural civilisation as a civilisation not strongly ruled by economy, we suggest for avoiding collapse 34 that only civilisations capable of such a switch from an economical society to a sort of “cultural” society in a timely manner, may survive. This discussion leads us to the conclusion that, even assuming the mediocrity principle, the answer to “Where is everybody?” could be a lugubrious “(almost) everyone is dead”.

Conclusions

In conclusion our model shows that a catastrophic collapse in human population, due to resource consumption, is the most likely scenario of the dynamical evolution based on current parameters. Adopting a combined deterministic and stochastic model we conclude from a statistical point of view that the probability that our civilisation survives itself is less than 10% in the most optimistic scenario. Calculations show that, maintaining the actual rate of population growth and resource consumption, in particular forest consumption, we have a few decades left before an irreversible collapse of our civilisation (see Fig.  5 ). Making the situation even worse, we stress once again that it is unrealistic to think that the decline of the population in a situation of strong environmental degradation would be a non-chaotic and well-ordered decline. This consideration leads to an even shorter remaining time. Admittedly, in our analysis, we assume parameters such as population growth and deforestation rate in our model as constant. This is a rough approximation which allows us to predict future scenarios based on current conditions. Nonetheless the resulting mean-times for a catastrophic outcome to occur, which are of the order of 2–4 decades (see Fig.  5 ), make this approximation acceptable, as it is hard to imagine, in absence of very strong collective efforts, big changes of these parameters to occur in such time scale. This interval of time seems to be out of our reach and incompatible with the actual rate of the resource consumption on Earth, although some fluctuations around this trend are possible 35 not only due to unforeseen effects of climate change but also to desirable human-driven reforestation. This scenario offers as well a plausible additional explanation to the fact that no signals from other civilisations are detected. In fact according to Eq. ( 16 ) the mean time to reach Dyson sphere depends on the ratio of the technological level T and therefore, assuming energy consumption (which scales with the size of the planet) as a proxy for T , such ratio is approximately independent of the size of the planet. Based on this observation and on the mediocrity principle, one could extend the results shown in this paper, and conclude that a generic civilisation has approximatively two centuries starting from its fully developed industrial age to reach the capability to spread through its own solar system. In fact, giving a very broad meaning to the concept of cultural civilisation as a civilisation not strongly ruled by economy, we suggest that only civilisations capable of a switch from an economical society to a sort of “cultural” society in a timely manner, may survive.

Waring, R. H. & Running, S. W. Forest Ecosystems: Analysis at Multiple Scales (Academic Press, 2007).

The State of the World’s Forests 2018. Forest Pathways to Sustainable Development, Food and Agriculture Organization of the United Nations Rome (2018).

Bologna, M. & Flores, J. C. A simple mathematical model of society collapse applied to Easter Island. EPL 81 , 48006 (2008).

Article   ADS   MathSciNet   Google Scholar  

Bologna, M., Chandia, K. J. & Flores, J. C. A non-linear mathematical model for a three species ecosystem: Hippos in Lake Edward. Journal of Theoretical Biology 389 , 83 (2016).

Article   MathSciNet   Google Scholar  

U.S. Energy Information Administration (EIA), https://www.eia.gov/international/data/world .

Vaclav, S. Energy transitions: history, requirements, prospects (ABC-CLIO, 2010).

Kardashev, N. Transmission of Information by Extraterrestrial civilisations. Soviet Astronomy 8 , 217 (1964).

ADS   Google Scholar  

Kardashev, N. On the Inevitability and the Possible Structures of Supercivilisations, The search for extraterrestrial life: Recent developments; Proceedings of the Symposium p. 497–504 (1985).

Statistical Review of World Energy source (2018).

NASA source https://svs.gsfc.nasa.gov/11393 .

Frank, A., Carroll-Nellenback, J., Alberti, M. & Kleidon, A. The Anthropocene Generalized: Evolution of Exo-Civilizations and Their Planetary Feedback. Astrobiology 18 , 503–517 (2018).

Article   ADS   CAS   Google Scholar  

Fort, J. & Mendez, V. Time-Delayed Theory of the Neolithic Transition in Europe. Phys. Rev. Lett. 82 , 867 (1999).

Molles, M. Ecology: Concepts and Applications (McGraw-Hill Higher Education, 1999).

Wilson, E. O. The Future of Life (Knopf, 2002).

Bongaarts, J. Human population growth and the demographic transition. Phil. Trans. R. Soc. B 364 , 2985–2990 (2009).

Article   Google Scholar  

Dyson, F. J. Search for Artificial Stellar Sources of Infra-Red Radiation. Science 131 , 1667–1668 (1960).

Bologna, M., Ascolani, G. & Grigolini, P. Density approach to ballistic anomalous diffusion: An exact analytical treatment. J. Math. Phys. 51 , 043303 (2010).

Hanggi, P. & Talkner, P. First-passage time problems for non-Markovian processes. Phys. Rev. A 32 , 1934 (1985).

Article   ADS   MathSciNet   CAS   Google Scholar  

Weiss G. H. Aspects and Applications of the Random Walk , (North Holland, 1994).

Moore, G. E. Cramming more components onto integrated circuits. Electronics 38 , 114 (1965).

Google Scholar  

Business Cycle Expansion and Contractions, https://web.archive.org/web/20090310081706/ ; http://www.nber.org/cycles.

Drake, F. The radio search for intelligent extraterrestrial life. In Current Aspects of Exobiology 323–345 (Pergamon Press, New York, 1965).

Burchell, M. J. W(h)ither the Drake equation? Intern. J. Astrobiology 5 , 243–250 (2006).

Article   ADS   Google Scholar  

Hart, M. H. Explanation for the Absence of Extraterrestrials on Earth. Quarterly Journal of the Royal Astronomical Society 16 , 128–135 (1975).

Freitas, R. A. There is no Fermi Paradox. Icarus 62 , 518–520 (1985).

Engler, J. O. & von Wehrden, H. Where is everybody?? An empirical appraisal of occurrence, prevalence and sustainability of technological species in the Universe. International Journal of Astrobiology 18 , 495–501 (2019).

Kolodny, O. & Feldman, M. W. A parsimonious neutral model suggests Neanderthal replacement was determined by migration and random species drift. Nature Comm. 8 , 1040 (2017).

Grimaldi, C. Signal coverage approach to the detection probability of hypothetical extraterrestrial emitters in the Milky Way. Sci. Rep. 7 , 46273 (2017).

Daly, H. E. & Farley, J. Ecological Economics, Second Edition: Principles and Applications )Island Press, 2011).

Paris Agreement, United Nations Framework Convention on Climate Change (UNFCCC) https://unfccc.int/files/meetings/paris_nov_2015/application/pdf/paris_agreement_english_.pdf.

Tol, R. S. J. The structure of the climate debate. Energy Policy 104 , 431–438 (2017).

Rood, R. T. & Trefil, S. J. Are we alone? The possibility of extraterrestrial civilisations (Scribner, 1981).

Kukla, A. Extraterrestrials A Philosophical Perspective (Lexington Books, 2010).

Strunz, S., Marselle, M. & Schröter, M. Leaving the “sustainability or collapse” narrative behind. Sustainability Science 14 , 1717–1728 (2019).

Song, X.-P. et al . Global land change from 1982 to 2016. Nature 560 , 639–643 (2018).

Download references

Acknowledgements

M.B. and G.A. acknowledge Phy. C.A. for logistical support.

Author information

These authors contributed equally: Mauro Bologna and Gerardo Aquino.

Authors and Affiliations

Departamento de Ingeniería Eléctrica-Electrónica, Universidad de Tarapacá, Arica, Chile

Mauro Bologna

The Alan Turing Institute, London, UK

Gerardo Aquino

University of Surrey, Guildford, UK

Goldsmiths, University of London, London, UK

You can also search for this author in PubMed   Google Scholar

Contributions

M.B. and G.A. equally contributed and reviewed the manuscript.

Corresponding author

Correspondence to Gerardo Aquino .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Bologna, M., Aquino, G. Deforestation and world population sustainability: a quantitative analysis. Sci Rep 10 , 7631 (2020). https://doi.org/10.1038/s41598-020-63657-6

Download citation

Received : 20 November 2019

Accepted : 02 April 2020

Published : 06 May 2020

DOI : https://doi.org/10.1038/s41598-020-63657-6

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Mathematical model to study the impact of anthropogenic activities on forest biomass and forest-dependent wildlife population.

• Ibrahim M. Fanuel
• Silas Mirau
• Francis Moyo

International Journal of Dynamics and Control (2024)

Future-proofing ecosystem restoration through enhancing adaptive capacity

• Marina Frietsch
• Jacqueline Loos
• Joern Fischer

Communications Biology (2023)

Degrowth: How Much is Needed?

• Ted Trainer

Biophysical Economics and Sustainability (2021)

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: Anthropocene newsletter — what matters in anthropocene research, free to your inbox weekly.

• Reference Manager
• Simple TEXT file

People also looked at

Original research article, understanding the socio-economic causes of deforestation: a global perspective.

• 1 Department of Economics, Czech University of Life Science, Prague, Czechia
• 2 Department of Trade and Finance, Czech University of Life Science, Prague, Czechia

Introduction: This paper investigates the links between deforestation and key economic, social, environmental, and geographical variables. We focus on per capita GDP, total forest cover, and the population across a diverse sample of countries from five continents for the last three decades.

Methods: This study utilizes a regression model using panel data to show the impact of key economic, and social variables on deforestation. Also, set of dummy variables is introduced in the paper. To enable the investigation, we use a set of dummies to capture their influence. The random effect specifications are used in this investigation. The research focuses on a period ranging from 1990 to 2020.

Results: Results show how different socio-economic variables influence deforestation. For example, disruptive events like the COVID-19 pandemic and the financial crisis had a negative effect on forest area development across all models. GDP per capita has different impact depending on the size of a country. Former colonies seem to have more deforestation.

Conclusions: The global environmental challenges posed by human activities and their impact on the state of forest have become increasingly evident. It is necessary to undertake policy and governance reforms to establish a solid legal framework, strengthen enforcement mechanisms, and foster transparency and accountability. The promotion of sustainable agriculture and agroforestry practices can substantially alleviate pressure on forests. Furthermore, it is necessary to mitigate disruptive events like pandemics by establishing specific strategies and creating contingency plans.

1. Introduction

Deforestation is raising concerns because of its negative consequences for example climate change, decrease in biodiversity, soil degradation, reduction of timber supply, floods, and siltation. Therefore it is a complex process that has impacts on both the environment and the economy ( Van Khuc et al., 2018 ). Any change in forest cover has both positive and negative effects on the local ecosystem and on the global environment ( Silva Junior et al., 2021 ). Destroying and degrading natural ecosystems lead to a decline in global biodiversity ( Angelsen and Kaimowitz, 1999 ). The problem of (a)deforestation is an example of a global externality ( Lawrence et al., 2022 ). Current research claims that it is needed to identify the specific economic factors that drive deforestation and develop effective policies and tools to mitigate its impacts at the global and national level ( Bhatia and Cumming, 2020 ; Ahmed et al., 2023 ).

Figures 1 , 2 offer a depiction of deforestation and afforestation trends. Through a comprehensive examination of global land cover changes for the years 1990 and 2020, the analysis brings to light the diverse and intricate shifts in forest cover. This exploration unveils distinct spatial and temporal fluctuations across various geographical regions. The Figures 1 , 2 effectively underscore the changing rates at which these transformations have emerged, highlighting the cases of rapid deforestation in certain regions juxtaposed with a rejuvenation of forested areas in others. This paper’s primary aim is to identify the underlying drivers that give rise to these contrasting trends.

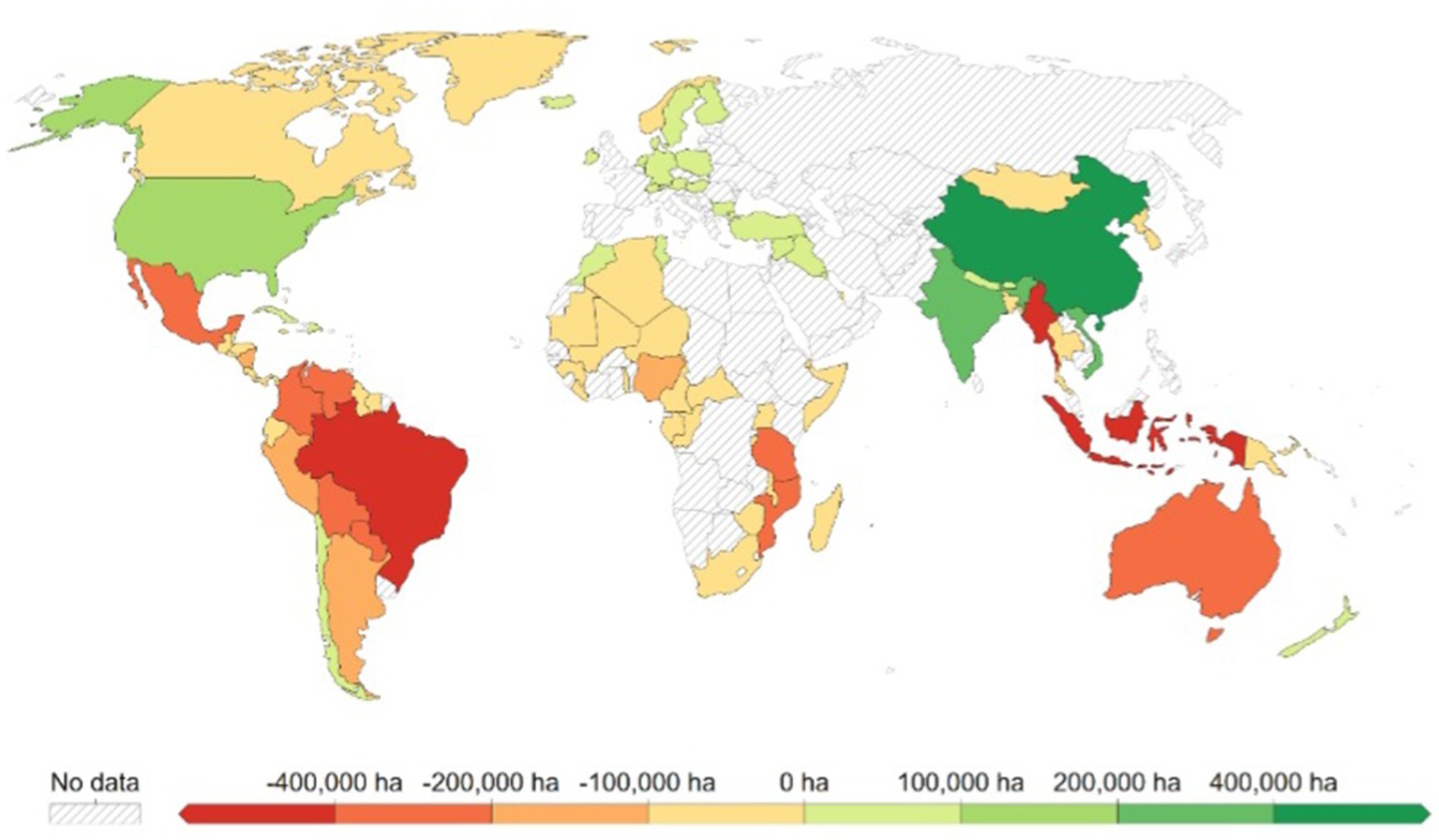
Figure 1 . Annual change in forest area (1995). Source: FAO (2020) and Our World in Data (2021) .

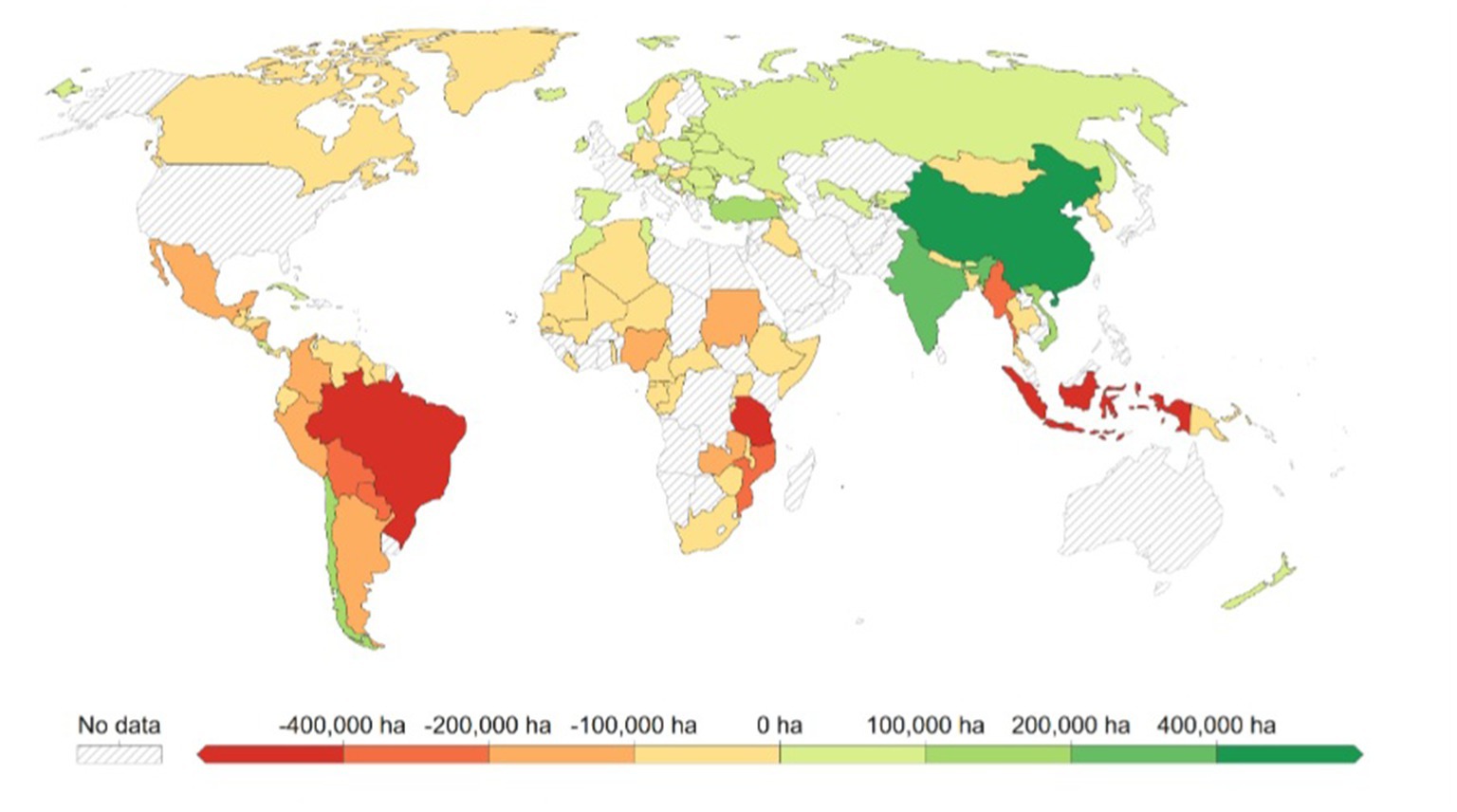
Figure 2 . Annual change in forest area (2020). Source: FAO (2020) and Our World in Data (2021) .

Various studies have raised arguments and hypotheses on the causes of deforestation. Studies are, however, often focused on smaller regions ( Maretto et al., 2020 ), individual states ( Zeb et al., 2019 ), or entire continents ( Leisher et al., 2013 ). The heterogeneity of countries and regions limits the significance and global impact of the results. As opposed to these studies, our study aims to contribute to the literature by systematic globally oriented research of the socio-economic drivers of deforestation. Previously published global studies are somewhat dated or do not include such a range of investigated variables ( Ehrhardt-Martinez, 1998 ; Ewers, 2006 ; Damette and Delacote, 2012 ; Nguyen et al., 2023 ).

Therefore, this paper aims to investigate the links between deforestation and various economic, social, environmental, and geographical factors, such as per capita GDP, total forest cover, and population. We look at these aspects across multiple countries from five continents over the past 30 years. We carefully select several countries to delve into these connections. We ensured a relatively even distribution of examples across Europe, Africa, Asia, and North America is present. Additionally, we include two instances from South America, chosen based on relevance and available data. The goal was to have a mix of both larger and smaller countries to achieve a diverse range of results.

Also, several major global events are incorporated in the investigation such as COVID-19 pandemic and financial crisis. To account for the impacts of these events on the variables being analysed, various dummy variables were included in the model. In addition to standard environmental and economic indicators, we also utilized dummy variables to account for factors such as a country’s location, EU membership, geographical position, continent, and landlock, in order to examine their potential impacts on deforestation rates. Data sources and the importance of the investigated factors are justified in the Data and Methodology section of this article. By incorporating these additional variables, our analysis seeks to provide a more comprehensive understanding of the complex factors contributing to deforestation in these selected countries and to help inform policy and decision-making aimed at reducing its impacts. Based on existing research gaps, we established the following research questions: (1) Which distinct factors wield the potential to mold the growth of forested regions? (2) Do relationships exist between deforestation and economic indicators, including their driving forces? and (3) Did significant global occurrences like the 2008–2010 financial crisis and the advent of the COVID-19 pandemic exert influence on variables tied to deforestation?

2. Literature review

The review of existing literature demonstrates that the reasons and catalysts behind deforestation have been extensively explored in the preceding decades. A consensus among numerous contemporary and historical studies is that the primary causes driving deforestation and forest deterioration encompass population upsurge, agricultural expansion, urban proliferation, and intensified fuelwood gathering, particularly within developing nations ( Jallat et al., 2021 ; Ahmed et al., 2023 ). Nonetheless, comprehending the root causes of deforestation is a more intricate undertaking. The distinct characteristics of continents, the varying levels of economic advancement, demographic shifts, and other indicators all contribute to a multifaceted picture.

According to Derouin (2019) , deforestation refers to the deliberate clearing of extensive tree-covered areas, primarily driven by human actions. Derouin (2019) identifies the following as factors contributing to deforestation: (1) Conversion of land for oil palm, soybeans, and other agricultural cultivation; (2) Expansion of farming areas in response to heightened worldwide requests for livestock-based commodities; (3) Advancement of urban zones, the establishment of new transportation networks, and housing projects; and (4) Generation of wood pulp intended for the paper sector, ultimately transformed into paper and cardboard goods.

In a study by Jayathilake et al. (2021) , commercial agriculture emerged as the primary force propelling deforestation in tropical nations, trailed by the expansion of infrastructure and settlement areas. Similarly, Curtis et al. (2018) highlighted land utilization for commodity production, agriculture, and forest fires as the foremost drivers behind worldwide deforestation. To combat this issue, Curtis proposes a solution to extract five million hectares of conversion annually from supply-customer chains, aiming to eliminate deforestation.

Amelung and Diehl (1992) assert that increasing cultivation stands as the primary catalyst for deforestation. These authors also underscore the role of a growing population in this dynamic. The notion that an expanding population contributes to deforestation is supported by various authors (e. g., Allen and Barnes, 1985 ; Cropper and Griffiths, 1994 ; Ehrhardt-Martinez, 1998 ; Mather and Needle, 2005 ). Martínez and Poveda (2021) emphasize that global attainment of economic and societal advancement has often come at the cost of environmental degradation.

Shafron (2019) examines the interplay between deforestation and social aspects of forest management. As highlighted by Ferrer Velasco et al. (2020) , deforestation frequently intertwines with human actions and can wield consequences on vital forest ecosystem services, encompassing carbon sequestration, biodiversity preservation, and water regulation.

Damette and Delacote (2012) found positive correlations between economic development, timber harvesting, demography, prices with deforestation. However, institutional quality was not found to significantly impact deforestation ( Damette and Delacote, 2012 ). In a distinct examination of deforestation’s causes in Vietnam, the authors proposed enhancements to the institutional framework. Their recommendations encompass poverty alleviation, conservation of existing forests, enhanced governance at the provincial level, and effective management of population growth ( Van Khuc et al., 2018 ). McCallister et al. (2022) suggest that institutional and economic factors of deforestation pose greater challenges for identification and control compared to conventional factors like livestock production, agricultural land expansion, and the mining industry.

The theoretical foundation underpinning the link between per capita income and deforestation is encapsulated by the U-shaped Kuznets Curve. This framework posits that in less developed nations, economic growth initially exerts a negative impact on the environment (evidenced by deforestation). However, at a certain threshold of GDP per capita , environmental degradation (including deforestation) reaches a point of saturation, ceasing to escalate with further economic expansion. This phenomenon may even lead to afforestation in more advanced economies ( Culas, 2007 ; Adila et al., 2021 ; Caravaggio, 2022 ).

Destiartono and Ekananda (2023) assessed GDP per capita in relation to deforestation across Southeast Asia, identifying a pivotal break-even point at $26,785. This juncture signifies the transition to an advanced stage of economic development and theoretically affirms the fundamental premise of the U-shaped curve. Interestingly, the study designates Brunei Darussalam as the sole Southeast Asian nation to have achieved a higher level of deforestation. Meanwhile, Ajanaku and Collins (2021) validated the Environmental Kuznets Curve hypothesis within Africa during the period spanning 1990 to 2016. Their analysis positioned the break-even point at $3,000.

Nguyen et al. (2023) conducted a study assessing the influence of tourism on forested areas across a diverse collection of 140 economies worldwide. Their findings indicate a favorable short-term impact of tourism, which, however, turns detrimental in the long run. Notably adverse consequences of tourism were particularly pronounced in Africa, Latin America, and the Caribbean. Another intriguing factor was explored by Nguyen and Nguyen (2023) . Their examination of a global sample spanning 148 countries from 1991 to 2017 revealed an asymmetrical long-term correlation between the shadow economy and deforestation. Brown and Pearce (2023) in their book examine different causes for tropical areas deforestation albeit most of the data is relatively old. Additionally, González-Eguino (2015) underscores the significance of illicit mining within the informal economy. These unauthorized activities often intertwine with poverty and a malfunctioning labor market ( Santos de Lima et al., 2018 ; Zeb et al., 2019 ).

3. Data and methodology

This study explores a regression model using panel data to show the impact of key economic, and social variables on deforestation. To enable the investigation, we use a set of dummies to capture their influence. The random effect specifications are used in this investigation.

3.1. Countries specification

The characteristics of deforestation trends and causes vary across continents and countries, as outlined in recent studies ( Antonarakis et al., 2022 ; Ma et al., 2023 ). In North America, deforestation rates have generally remained lower compared to other continents, especially in recent years. This can be attributed partially to effective forest management practices, the transition toward a more service-oriented economy, and dedicated reforestation efforts. Localized deforestation in this region can arise from urban expansion, wildfires, and insect infestations ( Zerriffi et al., 2023 ).

On the other hand, South America, which hosts the Amazon rainforest, experiences some of the highest deforestation rates worldwide. This is primarily fueled by agricultural expansion, notably for beef and soy production, alongside mining and infrastructure growth. Deforestation in this context is also influenced by governance issues and insufficient enforcement of environmental regulations ( Silva Junior et al., 2021 ; Stabile et al., 2022 ).

Deforestation rates across Asia are shaped by a diverse array of influences. For instance, in Southeast Asia, the expansion of palm oil plantations stands out as a prominent cause of deforestation ( Miettinen et al., 2014 ; Van Khuc et al., 2018 ). In various other Asian regions, the noteworthy drivers encompass urban sprawl, infrastructure advancement, and timber extraction ( Khalid et al., 2019 ).

Meanwhile, Europe has generally witnessed a growth in its forest cover over recent decades, largely attributable to sustainable forest management practices and concerted reforestation initiatives. While issues like urban expansion and, in certain areas, heightened demand for bioenergy can lead to localized deforestation, the predominant forces behind deforestation in this context include agricultural expansion, urbanization, and timber logging ( Belušić et al., 2019 ; Strandberg and Kjellström, 2019 ).

To comprehensively address the matter and ensure a well-rounded representation, we have selected a minimum of five countries from each continent. This selection process was purposefully designed to encompass nations of varying sizes, thus revealing the inclusion of both substantial and smaller countries. The overarching objective was to achieve a comprehensive cross-section of human development levels across the global spectrum.

Our approach also prioritized the incorporation of both developed and developing countries, along with nations exhibiting a broad range of economic and social development statuses. The guiding principle behind our country selection was based on the purpose to assemble a sample that authentically reflects the complex set of factors influencing economic and social development across different parts of the world, in line with the directives provided by the World Bank (2023) . A detailed list of the countries chosen for our analysis is in Table 1 .

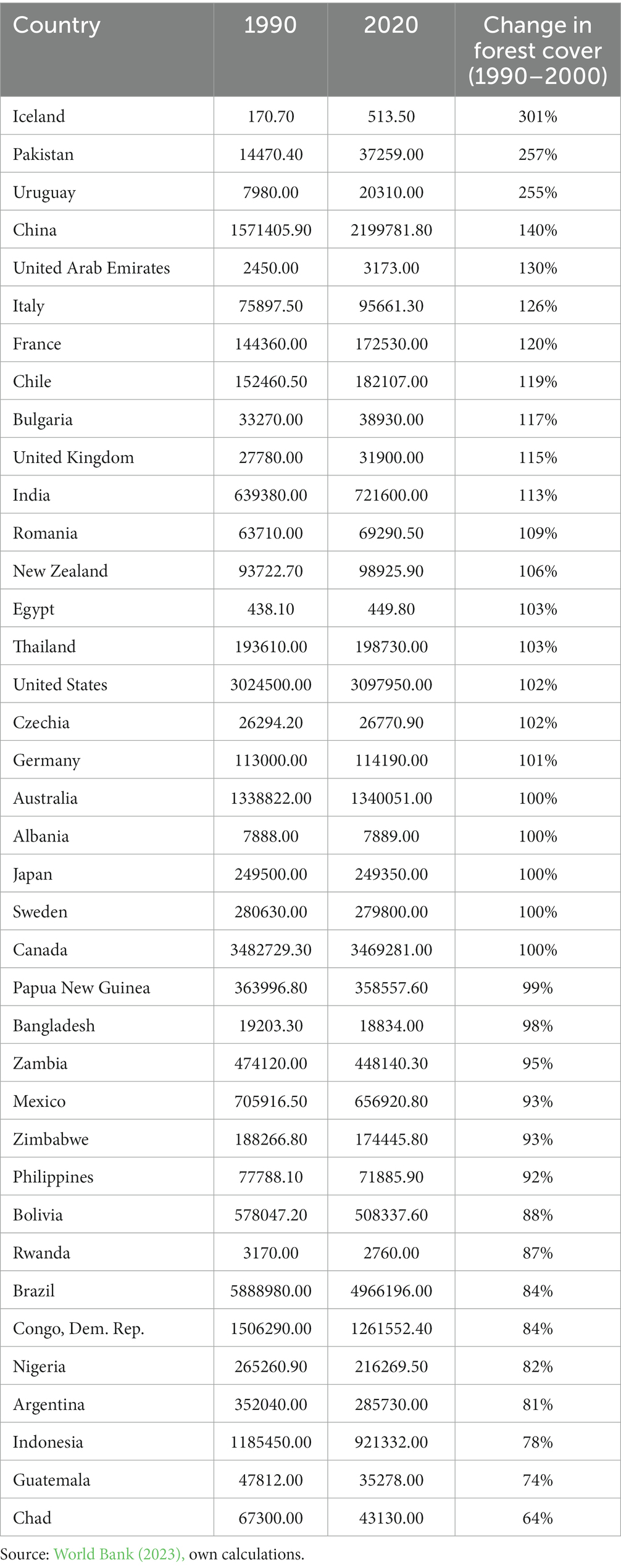
Table 1 . Countries selected for analysis ranked by change in forest cover.

In our research, we introduced colonial countries as a dummy variable to assess their potential influence on deforestation rates within the chosen nations. This inclusion was motivated by the recognition that colonialism has been associated with enduring ramifications on a country’s economic and political structures. Colonialism was potentially influencing subordinate countries’ approaches to managing natural resources.

Drawing from the definition that designates a nation as landlocked if it is surrounded by other countries without direct sea access or if its coastline is located within a closed drainage basin, our team engaged in deliberations regarding the specific landlocked status of a particular country. Upon thorough consideration, we collectively arrived at a consensus and determined the countries that fit the landlocked classification. Currently, the global count stands at 44 landlocked countries, accompanied by 5 partially recognized landlocked territories ( The Fact File, 2022 ). The distribution between landlocked and non-landlocked nations intertwines with trade, economic, climatic, and environmental factors.

Non-landlocked countries, possessing unhindered access to maritime trade routes, enjoy the potential to exploit and export timber and other forest resources, possibly leading to heightened rates of deforestation driven by economic motives. Conversely, landlocked countries, constrained by the absence of direct sea route access, might exhibit reduced incentives for large-scale logging intended for export purposes and increased deforestation.

Nations without direct sea access frequently encounter distinct economic obstacles, such as escalated transportation expenses and increased trade overheads. In response, these countries may resort to the exploitation of natural assets, including forests, as a strategy for economic advancement. Landlocked countries could potentially rely more significantly on land-based resources, notably forests, as integral components of their sustenance. Consequently, this reliance might contribute to elevated deforestation rates, driven by the inhabitant’s utilization of forest resources for necessities like fuel, sustenance, and construction materials.

3.2. Socio-economic indicators

3.2.1. gdp per capita in ppp.

The economic metric of GDP per capita at purchasing power parity (PPP) serves as an indicator of a nation’s level of development. Often, countries with elevated GDP per capita possess more resources that can be allocated toward sustainable practices and the preservation of forests ( Ewers, 2006 ). Nonetheless, it’s plausible that countries achieving higher GDP per capita levels might have experienced industrialization processes that could entail deforestation ( Martínez and Poveda, 2021 ). The correlation between GDP per capita and deforestation finds its theoretical framework within the Kuznets curve ( Ajanaku and Collins, 2021 ). This concept was thoroughly explored in our literature review.

The data utilized in this paper pertains to GDP per capita measured through purchasing power parity (PPP), which is converted into international dollars using purchasing power parity rates. This approach considers the fact that equivalent monetary amounts can yield different purchasing capabilities for goods and services in different countries. The dataset originates from the International Comparison Program (ICP) administered by the World Bank and the Eurostat-OECD PPP Program.

This data is gathered on an annual basis and reported in terms of international dollars. The methodology for aggregation involves a weighted average. Specifically, the data’s definition underscores that Gross Domestic Product (GDP) at purchaser’s rates comprises the total value added by all domestic producers within the country, along with any taxes on products, while subtracting any subsidies not included in the product’s value. However, this computation does not include the depreciation of manufactured assets or the depletion and deterioration of natural resources. In essence, this dataset yields invaluable insights into the economic welfare of nations, adjusting disparities in prices and expenses across different countries ( World Bank, 2023 ).

3.2.2. Population

Population size plays a pivotal role in both forestation and deforestation dynamics. Larger populations often induce a higher pressure on forest resources, thereby contributing to deforestation. Nonetheless, there are instances where population growth induces reforestation activities, as societies increasingly recognize the significance of forests and implement measures to safeguard and expand them ( Carr et al., 2005 ; Oyetunji et al., 2020 ).

The provided data offers an approximation of the overall population, encompassing all residents within a country, irrespective of their citizenship or legal status. This dataset is sourced from diverse resources, including census records, statistical publications, and demographic modeling undertaken by the United Nations Population Division and the U.S. Census Bureau. The aggregation process involves summing up population estimates across all l.

Fluctuations in population size can wield substantial influences over natural resources and social infrastructure. At the same time, population growth can trigger significant impacts while a reduction in population size may affect governmental services and infrastructure provisioning.

Gender disaggregation of Gender-specific breakdown of population data aids countries in forecasting the demand for social services with a focus on gender-related aspects. The total population data predominantly relies on national population censuses, supplemented by estimates for years preceding and following these censuses, obtained through demographic modeling. The accuracy and reliability of demographic insights are subject to diverse influences, including public confidence in the government, the government’s commitment to thorough and accurate enumeration, and the availability of supplementary data from surveys or registration systems.

Ensuring comparability among population indicators has some limitations due to disparities in concepts, definitions, and estimation methodologies used by different organizations. The intricate matter of international migration significantly contributes to population growth; however, estimating migration proves challenging due to differences in standards and the absence of comprehensive data.

Population projections until 2050 are constructed based on assumptions due to mortality, fertility, and migration, stratified by age and gender. These assumptions draw from the UN Population Division’s World Population Prospects database medium variant ( World Bank, 2023 ).

3.2.3. COVID-19 impact and the financial crisis

Profound global events have a substantial influence over economic activities and, consequently, reverberate through the domains of forestation and deforestation ( Elliott, 2011 ). As an illustration, economic downturns can spur heightened logging activities as nations strive to fortify their economies. During the analysis timeframe, noteworthy global occurrences unfolded, including the 2008–2010 financial crisis and the onset of the COVID-19 pandemic in 2020 ( Uğurlu and Jindřichovská, 2022 ). In order to factor in the repercussions of these events on the variables under examination, the model incorporated dummy variables.

COVID-19 Crisis: The far-reaching impact of the COVID-19 pandemic extends to all forms of existence, including environmental stewardship. This crisis potentially triggered reduced human presence within forested areas, leading to a deceleration in deforestation rates ( Antonarakis et al., 2022 ). Conversely, the economic strains caused by the pandemic might have propelled certain individuals or entities to intensify logging endeavors ( Vale et al., 2021 ; Céspedes et al., 2022 ).

The financial crisis, originating in the United States and spreading across nations, had significant repercussions on the worldwide economy, initiating declines in economic growth, employment levels, and financial stability. To encompass the crisis’s effects, a dummy variable was introduced to encapsulate the years 2008 through 2010, coinciding with the crisis’s most severe impact.

Likewise, the COVID-19 pandemic had a profound influence globally, prompting governments to adopt diverse measures to curb its transmission and alleviate its impact on both the economy and society ( Jindřichovská and Uğurlu, 2021 ). To accommodate these effects, a dummy variable was established to denote the year 2020, which marked the period when the pandemic most significantly influenced the variables under scrutiny ( Our World in Data, 2023 ).

3.3. Forest cover

Ewers (2006) discovered that nations with limited forests and lower income levels exhibit higher deforestation rates, while conversely, higher-income countries tend to maintain their forest coverage and may even plant new forested areas. Notably, the deforestation patterns of countries with substantial forest resources appear to be less influenced by their GDP per capita .

The chosen dataset for this research, representing the environmental condition, focuses on forest land cover. The time span encompasses the years from 1990 to 2020, with measurements in square kilometers. This information is sourced from the World Bank’s online repository. According to the dataset specifications provided by the World Bank, the forest cover under consideration encompasses natural or planted stands of at least 5 meters in height, whether in productive use or not. This definition excludes stands within agricultural production systems like orchards and agroforestry setups, as well as urban parks and gardens.

For our study, deforestation data from the Food and Agriculture Organization (FAO) was utilized, sourced through their global Forest Resources Assessment (FRA) program, an initiative operational since 1946. The FAO periodically assembles and assesses forest cover details at various levels: subregional, regional, and global. The dataset furnishes information regarding forested areas and their temporal changes, albeit without accounting for areas subject to logging, degradation due to fuelwood collection, acid precipitation, or forest fires.

The FAO employs a consistent forest definition, necessitating the presence of trees and the exclusion of dominant land uses, with a minimum tree height of 5 meters. It is important to note that the data might not precisely reflect the actual rate of deforestation in certain countries, as it does not differentiate between natural forests and plantations ( World Bank, 2023 ).

3.4. Methodology

For the purposes of this paper, the authors employ panel regression analysis as the chosen method. The method of panel regression is used for the following reasons. Panel regression offers the capability to manage unobserved variables that exhibit temporal variation but remain consistent across different entities, or those that display entity-specific variation without temporal changes. This proves particularly advantageous in the context of studying deforestation trends across various countries and time periods, considering the potential influence of unobserved factors unique to specific countries or periods. Furthermore, panel regression effectively accommodates individual heterogeneity, a vital consideration when dealing with data from diverse countries, each with distinct characteristics. Unlike linear regression, panel regression yields more informative data, heightened variability, reduced collinearity among variables, increased degrees of freedom, and enhanced efficiency. Scrieciu (2007) endorses panel regression as a suitable tool for examining deforestation factors in international comparisons.

Panel regression constitutes a modeling technique suitable for panel data, also referred to as longitudinal or cross-sectional data. It finds common usage in tracking the behavior of statistical entities (termed panel units) over a temporal trajectory, with these entities corresponding to the countries outlined in Table 1 . This approach allows for the control of both panel unit and time effects while estimating regression coefficients ( Torres-Reyna, 2007 ). In the context of regression analysis involving cross-sectional data, parameter estimation is typically conducted using the Ordinary Least Squares (OLS) method. The Best Linear Unbiased Estimation (BLUE) provides an optimal linear and unbiased estimation. In this paper, panel data encompasses information about a group of countries observed concurrently. The dataset spans T time periods ( t  = 1, 2…, T ) from 1990 to 2020 and includes N units ( I  = 1, 2…, N ), representing 38 countries across 5 continents. This results in a total of N × T observation units within the panel data.

The data used are summarized in the Table 2 .

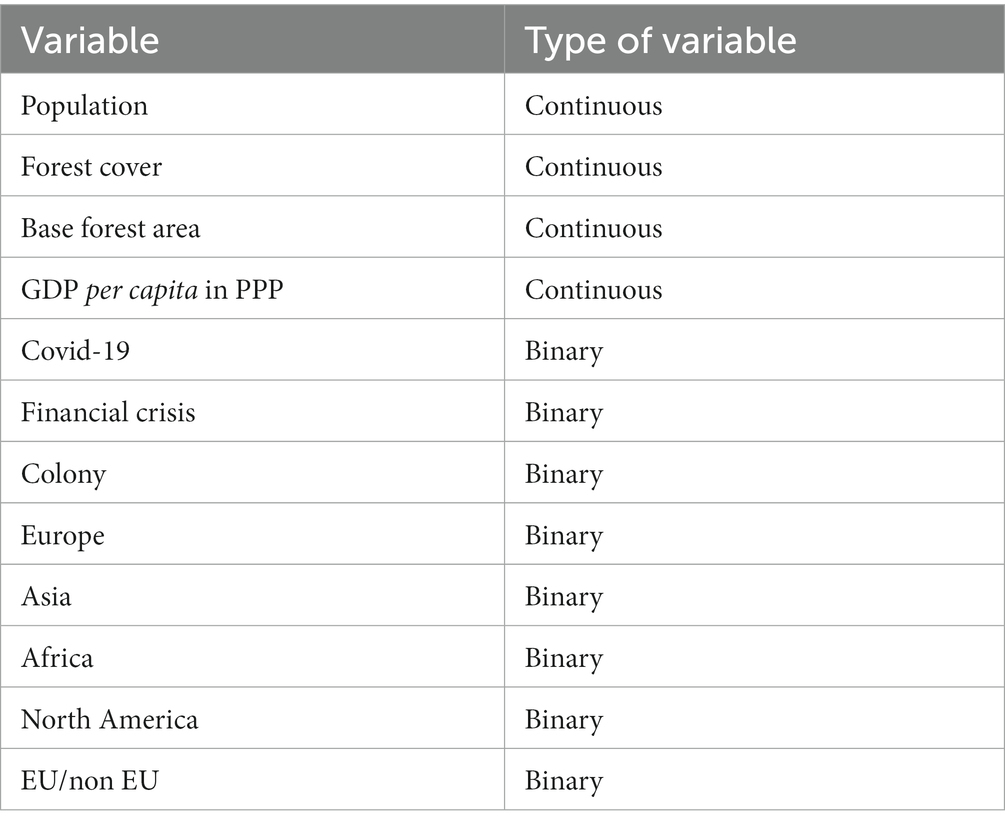
Table 2 . Variables used in the model.

The Table 2 shows which variables are continuous in nature. These were taken from publicly available sources such as World Bank (2023) or FAO (2020) . Binary variables take the value 1 if it is true or 0 otherwise.

For the analysis, the random effects model was chosen. The rationale behind random effects models is that, unlike fixed effects models, the variation among entities is assumed to be random and unrelated to the predictor or independent variables included in the model.

The random effects model is specified as:

where u it is the inter-entity error, e it presents the intra-entity error, and all remaining variables retain their previous definitions. To determine the most suitable model, the authors performed a series of tests including the F test, the Breusch-Pagan test, and the Hausman test.

As already discussed, this research paper explores the Forest Area variable as the dependent variable, seeking to elucidate the precise factors influencing its development. Firstly, Hausman test was performed, validating the random effects model’s applicability ( p  = 0.157078, Chi-square(12) = 16.8051).

Panel regression findings are detailed in the ensuing tables, with Table 3 presenting the first model (referred as Model 1) encompassing all variables within the complete dataset. The model includes 1,178 observations. During model compilation, certain chosen variables emerged as statistically insignificant, termed superfluous variables, and were consequently removed. These variables include EU/non-EU, Landlocked, Southern Hemisphere, and Africa.

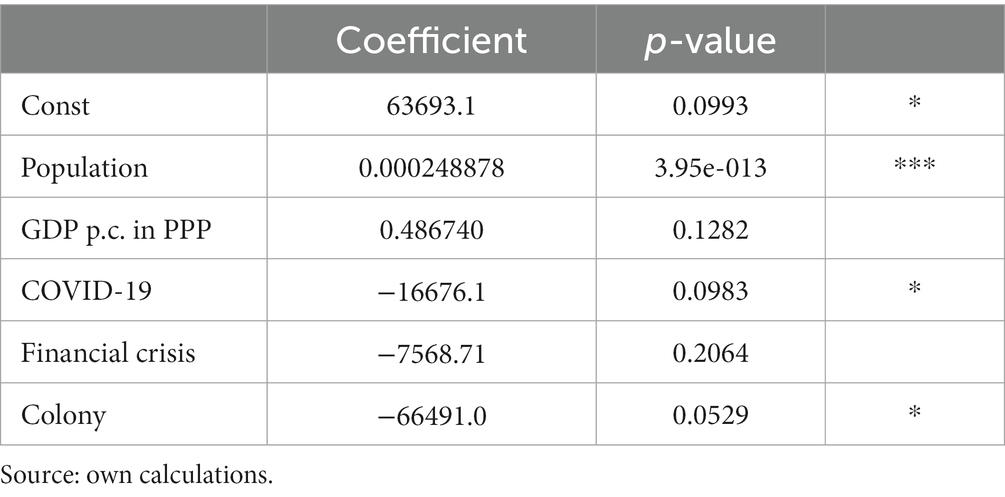
Table 3 . Deforestation: complete data (Model 1).

In the Gretl program-generated model, statistically significant relationships are denoted by stars. One star represents a 10% significance level, two stars signify a 5% level, and three stars indicate a 1% level. The selection of significance level ( p -value) for model evaluation corresponds to the test’s conservativeness – the lower the chosen significance, the more conservative the test. Population totals exhibit statistical significance at the 1% level. As indicated by Model 1, it appears that an increase in population totals is accompanied by a corresponding growth in forest area. Specifically, according to this model, a one-unit rise in population leads to a forest area expansion of 248 m 2 . Similarly, should GDP per Capita in PPP experience a one-unit increase, the forest coverage is projected to expand by 486.740 m 2 . However, it’s worth noting that these variable exhibits statistical significance at the 13% level, which raises concerns about its reliability. Another variable lacking significance in the model is the financial crisis spanning from 2008 to 2010. Furthermore, the COVID-19 crisis, represented by its dummy variable accounting for 2020, is found to have a negative impact significant at the 10% level. This would imply that during COVID-19, deforestation was happening. The historical colonization status of a country appears to exert a noteworthy influence, significant at the 10% level. Colonized nations exhibit a comparatively reduced forest area, measuring 66.491 km 2 , in contrast to countries not subjected to colonization, as defined in the preceding “Data” chapter. To establish the appropriateness of tested models, the Akaike criterion and Hannan-Quinn were employed for model comparisons. The analysis determined that the current model is the most suitable one, and no further refinements could enhance its performance level.

The characteristics and results of the second and third models are depicted in Tables 4 , 5 . Table 4 specifically presents countries with a forest area exceeding 1 million square kilometers. Model 2 includes 186 observations (6 countries), exclusively tied to the development of nations possessing over 1 million km 2 of forest area. Given the relatively modest sample size, certain variables had to be omitted, including EU/non-EU, Colony, Landlocked, Southern hemisphere, as well as Asia, Europe, North America, Africa, and the 2008 Financial crisis.

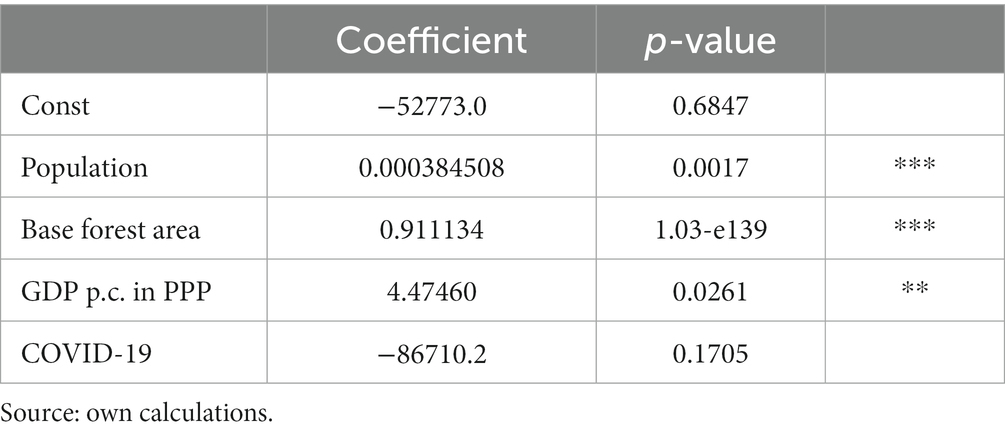
Table 4 . Estimation for countries with forest area greater than 1 million km 2 (Model 2).

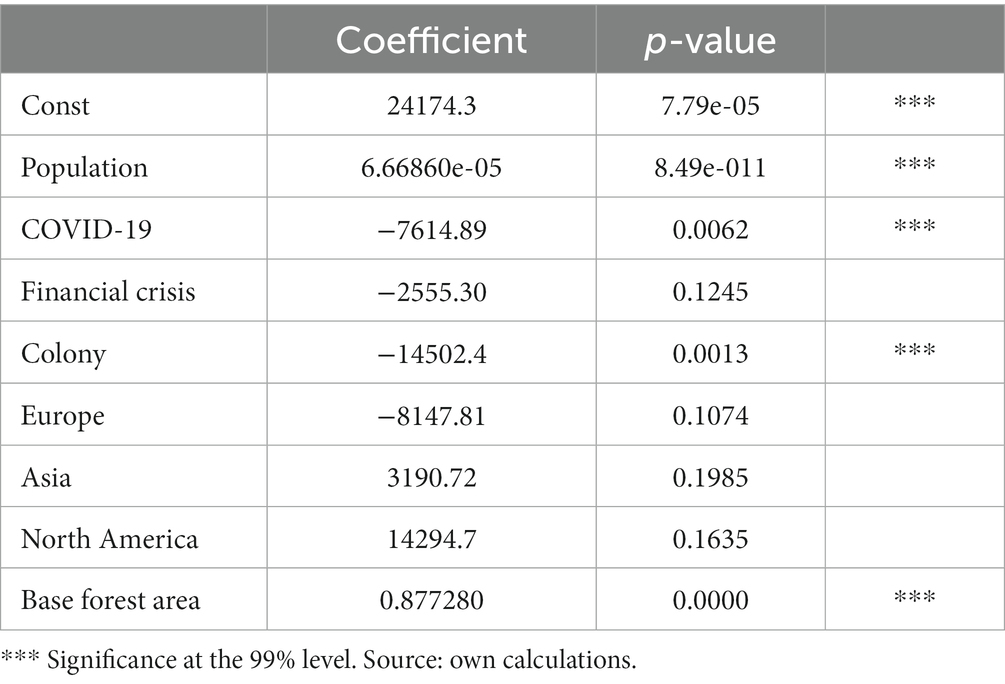
Table 5 . Deforestation of countries with less than 1 million km 2 of forest area (Model 3).

Indonesia stands as the sole country included in both models – encompassing nations with forest areas surpassing 1 million km 2 (Model 2) and those with less than 1 million km 2 (Model 3). The choice to include Indonesia derives from its fluctuating forest cover, spanning from 1,185,450 km 2 in 1990 to 921,332 km 2 in 2020.

The magnitude of forest area in countries with forest covers exceeding 1 million km 2 appears notably influenced by the variables Population and GDP per capita . At a significance level of 1%, the population demonstrates a substantial influence on forest area in countries boasting more than 1 million km 2 of forest coverage. A population increase of 1 unit corresponds to a forest area expansion of 384 m 2 , a value surpassing that observed in Model 1. Counterintuitively, despite expectations of a negative correlation between larger populations and reduced forest areas, these models propose a contrary relationship. This phenomenon is primarily attributed to the pronounced influence of China and India, both marked by substantial populations and extensive forest areas. The Base Forest area variable (shows area in 1990) depicts that since the first measurement, the forest area grew by 911,134 m 2 yearly on average in countries with more than 1 million km 2 of forest area.

At a 5% significance level, the model indicates that an increase in GDP per capita in PPP is associated with a forest area expansion of 44,746 km 2 . Notably, the variable GDP per capita displayed insignificance in the preceding Model 1. Over the course of the global COVID-19 pandemic, which the models incorporate as a dummy variable capturing its effects in 2020, deforestation ensued. Nevertheless, this variable emerges as statistically insignificant. These outcomes may substantially stem from the outsized influence of each country’s data within the dataset, given the inclusion of only 6 countries. This influence is underscored by instances such as Brazil, which experienced an annual change of 11,789 km 2 in 2019/20.

For reasons elucidated in the preceding section, Model 3 is a result of categorizing the chosen countries into two extensive groups based on their forest cover extents. Model 3 is based on the 992 observations bound solemnly to the figures connected to the deforestation of countries with less than 1 million km 2 of forest area. This model estimation results are depicted the Table 5 . The following variables have proven to be statistically largely insignificant (superfluous), so they were not included in the model: GDP per Capita in PPP, EU/non-EU, Landlocked, Southern hemisphere, and Africa.

For the reasons mentioned in the previous section describing Model 2: Indonesia is the only country, which was included in both models – Model 2 and Model 3. According to the model’s results, population, the impact of COVID-19, whether it has been a colony or not and the base forest area are all significant variables on the level of significance 1%. In these countries, the coefficient denoting the positive influence of population on forest area is notably smaller compared to the model involving countries with forest areas exceeding 1 million km 2 . A unit increase in population is associated with a mere 66.6 m 2 growth in the forest area.

The COVID-19 pandemic exhibited an adverse effect on forest area figures. However, it becomes evident that within the comprehensive Model 1, the pronounced coefficient was driven by countries endowed with expansive forest regions. This observation is supported by the coefficient in Model 3 (−7,614.89), which is approximately half that of the global dataset in the Model 1 (−16,676.1), and roughly one-tenth of the coefficient in Model 2 (−86,710.2). In the context of countries with forest areas less than 1 million km 2 , the variable “colony” emerges as significant. Colonized countries, on average, exhibit a smaller forest area per km 2 compared to their non-colonized counterparts. Divergence is evident in the outcomes related to the core forest area variable when compared to the expansive country Model 2. This discrepancy suggests that the pace of forest area growth is more gradual, averaging 877.280 m 2 to 911.134 m 2 annually, in countries with forest areas exceeding 1 million km 2 .

In the formulation of Model 4, 403 observations were employed for countries that experienced deforestation of 5% or more between 1990 and 2020. Results of model estimated are depicted in the Table 6 .

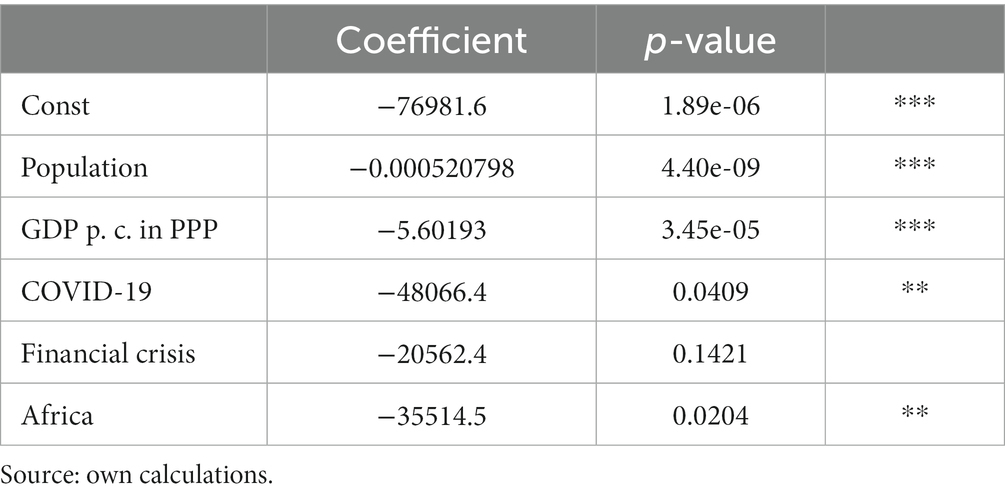
Table 6 . Deforestation of countries that deforested 5% and more from 1990 compared to 2020 (Model 4).

Several variables exhibited large statistical insignificance, prompting their removal from the model: EU/non-EU, Landlocked, Asia, and Europe. The variables Colony and Southern Hemisphere were automatically excluded from the model due to precise collinearity. Several variables have demonstrated significance at the 1% level: Population, GDP per capita in PPP, Africa, and COVID-19. This particular model, among the four incorporated within this study, presents the sole instance suggesting a negative relationship between forest area and GDP per capita in PPP and population. An increase in a country’s population by 1 unit is associated with a forest area reduction of 0.000520798 km 2 (equivalent to 520.8 m 2 ). Similarly, a 1-unit growth in GDP per capita leads to a forest area contraction of approximately 5.6 km 2 . The COVID-19 pandemic also manifests a detrimental influence on forest areas, substantiated at a 5% significance level. Although a discernible effect is observable concerning the 2008 financial crisis variable, it seems to hold limited significance.

From the selected variables, North America and base forest area stand as the sole contributors to a positive impact on a country’s forest area. Notably, North America underscores that countries situated within the region tend to exhibit substantial forest coverage. This phenomenon is driven by the inclusion of the USA and Canada within North America, both of which are sizable countries, thereby fostering larger forest areas in comparison to other nations.

5. Discussion, conclusions, and recommendations

Addressing the central research inquiry regarding the influence of selected socio-economic developmental indicators on deforestation across the chosen countries is not straightforward, given observed variations between smaller and larger nations concerning forest reserves. The impact of GDP remains ambiguous. Nevertheless, estimation outcomes for countries experiencing substantial forest loss align with prevailing literature, quantifying the contrast between economic development and environmental well-being.

Disruptive events like the COVID-19 pandemic and the 2008 financial crisis resoundingly reverberated, yielding a marked negative effect on forest area development across all models. It’s noteworthy to emphasize that, particularly within countries encompassing forest areas surpassing 1 million km 2 , the impact of the COVID-19 crisis was notably more pronounced than in nations with forest areas below 1 million km 2 .

In the temporal context spanning from 1990 to 2020 on a global scale, our model underscores the statistical significance of the population variable. The initial three models incorporated within this study suggest a positive association between population and forest area, indicating that an increase in one is accompanied by a rise in the other. However, divergent perspectives emerge from other scholars. Amelung and Diehl (1992) identified a negative impact of population growth on forest area. This observation aligns with multiple studies, including Allen and Barnes (1985) , Cropper and Griffiths (1994) , Ehrhardt-Martinez (1998) , and Mather and Needle (2005) . Such findings are also echoed in the conclusive model of countries that experienced deforestation of 5% or more over the preceding three decades. Discrepancies in outcomes might arise from the specific set of countries under examination. Additionally, Brown and Pearce (2023) claim that forest cover is negatively correlated with population.

Throughout the investigation, the authors encountered various studies concentrating on similar topics but confined to narrower geographical contexts. Austin et al. (2019) explored Indonesia, while Barbier and Burgess (2008) focused on tropical regions, and Silva Junior et al. (2021) delved into Amazon deforestation.

GDP per capita has demonstrated its relevance as a significant variable within countries having forest areas exceeding 1 million km 2 . These findings imply that the economic expansion of a nation is associated with a favorable effect on its forest area. However, contrasting findings are presented by Martínez and Poveda (2021) , who contend that global economic and social advancement has been achieved at the expense of environmental well-being. Conversely, divergent outcomes arise from the model exclusively encompassing countries that have experienced deforestation at a scale of 5% or more from 1990 to 2020. Within this context, the results unequivocally assert a negative influence of GDP per capita growth in PPP on the forest area.

In contrast to the conclusions drawn by Antonarakis et al. (2022) , the COVID-19 pandemic has yielded adverse effects on forest cover as evidenced by the models formulated in this study. These observations correspond to the findings of Vale et al. (2021) . As posited by Céspedes et al. (2022) , while numerous studies conducted in 2020 have predominantly concentrated on the immediate repercussions of the COVID-19 pandemic and its implications for deforestation rates, the focus should now shift toward the recuperation strategies employed by economies and the potential short- to long-term repercussions they may impact on forest cover.

The relevance of whether a country has undergone colonization emerges primarily in the context of countries with forest areas of less than 1 million km 2 . This distinction is rational considering that our dataset primarily encompasses these smaller colonized nations. Consequently, this variable attains significance. In an investigative endeavor, Marchand (2016) explores not only the influence of a colonial legacy on a country’s deforestation patterns but also the variations that exist in the inherited legacies.

This study has yielded a series of recommendations aimed at effectively addressing deforestation and promoting sustainable land management practices. It is imperative to undertake policy and governance reforms to establish a solid legal framework, strengthen enforcement mechanisms, and foster transparency and accountability. Engaging local communities and stakeholders in decision-making processes is pivotal to ensuring sustained success. The promotion of sustainable agriculture and agroforestry practices can substantially alleviate pressure on forests. Disciplines like agroecology, organic farming, integrated pest management, as well as the adoption of diversified cropping systems and agroforestry, can enhance productivity while concurrently safeguarding forests. Notably, the implementation of large-scale forest restoration and reforestation initiatives, utilizing indigenous tree species and involving local communities, as seen in instances such as China and India based on our dataset, is advisable. Collaborative efforts with non-governmental organizations (NGOs) and international entities can strengthen and amplify the impact of these initiatives. Based on this study, it is recommendable that adaptive policies for varied country sizes are developed. These policies should account for the varying impact of socio-economic indicators on deforestation between smaller and larger nations due to differences in forest reserves. Furthermore, it is necessary to mitigate disruptive events like pandemics by establishing specific strategies and creating contingency plans. This will ensure the resilience of forest ecosystems, and promote sustainable resource management during and after crises. Additionally, it is advisable to prioritize post-crisis recovery plans that integrate forest protection and restoration as part of broader economic recovery efforts. These recommendations address the complexity of factors influencing deforestation, including country size, disruptive events, and the need for adaptable policies to balance economic development with environmental conservation. However, this study does acknowledge certain limitations and suggests potential directions for future research. While the current paper has centered on economic, social, environmental, and geographical variables, further investigations could delve into the institutional and political determinants driving deforestation and afforestation. Additionally, the inclusion of qualitative insights from guided interviews with pertinent stakeholders from public, non-profit, and corporate sectors could enrich the analysis.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

PP: Conceptualization, Formal analysis, Investigation, Methodology, Resources, Supervision, Validation, Writing – original draft, Writing – review & editing, Data curation. JA: Conceptualization, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. JC: Data curation, Formal analysis, Investigation, Methodology, Validation, Writing – original draft, Writing – review & editing. LK: Data curation, Formal analysis, Writing – original draft, Writing – review & editing. PS: Data curation, Formal analysis, Writing – original draft, Writing – review & editing. DB: Data curation, Formal analysis, Writing – original draft, Writing – review & editing. J-MF: Data curation, Formal analysis, Writing – original draft, Writing – review & editing. EJ: Data curation, Formal analysis, Writing – original draft, Writing – review & editing. SP: Data curation, Formal analysis, Writing – original draft, Writing – review & editing. JS: Data curation, Formal analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review & editing. LS: Conceptualization, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Validation, Writing – original draft, Writing – review & editing.

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This article was supported by the Czech Universtity of Life Science (Faculty of Economics and Management) Internal Grant Agency, project number: 2022B0005.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Adila, D., Nuryartono, N., and Oak, M. (2021). The environmental Kuznets curve for deforestation in Indonesia. Econ. Financ. Indones. 67:195. doi: 10.47291/efi.v67i2.671

CrossRef Full Text | Google Scholar

Ahmed, H., Jallat, H., Hussain, E., Saqib, N. U., Saqib, Z., Khokhar, M. F., et al. (2023). Quantitative assessment of deforestation and forest degradation in Margalla Hills National Park (MHNP): employing landsat data and socio-economic survey. Forests 14:201. doi: 10.3390/f14020201

Ajanaku, B. A., and Collins, A. R. (2021). Economic growth and deforestation in African countries: is the environmental Kuznets curve hypothesis applicable? Forest Policy Econ. 129:102488. doi: 10.1016/j.forpol.2021.102488

Allen, J. C., and Barnes, D. F. (1985). The causes of deforestation in developing countries. Ann. Assoc. Am. Geogr. 75, 163–184. doi: 10.1111/j.1467-8306.1985.tb00079x

Amelung, T., and Diehl, M. (1992). Deforestation of tropical rainforests: economic causes and impact on development . Kiel, Tübingen: Institut für Weltwirtschaft, JCB Mohr.

Google Scholar

Angelsen, A., and Kaimowitz, D. (1999). Rethinking the causes of deforestation: lessons from economic models. World Bank Res. Obs. 14, 73–98. doi: 10.1093/wbro/14.1.73

PubMed Abstract | CrossRef Full Text | Google Scholar

Antonarakis, A. S., Pacca, L., and Antoniades, A. (2022). The effect of financial crises on deforestation: a global and regional panel data analysis. Sustain. Sci. 17, 1037–1057. doi: 10.1007/s11625-021-01086-8

Austin, K. G., Schwantes, A., Gu, Y., and Kasibhatla, P. S. (2019). What causes deforestation in Indonesia? Environ. Res. Lett. 14:024007. doi: 10.1088/1748-9326/aaf6db

Barbier, E. B., and Burgess, J. C. (2008). The economics of tropical deforestation. J. Econ. Surv. 15, 413–433. doi: 10.1111/1467-6419.00144

Belušić, D., Fuentes-Franco, R., Strandberg, G., and Jukimenko, A. (2019). Afforestation reduces cyclone intensity and precipitation extremes over Europe. Environ. Res. Lett. 14, 1–11. doi: 10.1088/1748-9326/ab23b2

Bhatia, N., and Cumming, G. S. (2020). Deforestation and economic growth trends on oceanic islands highlight the need for meso-scale analysis and improved mid-range theory in conservation. Ecol. Soc. 25, 1–14. doi: 10.5751/ES-11713-250310

Brown, K., and Pearce, D. W. (Eds.) (2023). The causes of tropical deforestation: the economic and statistical analysis of factors giving rise to the loss of the tropical forests . London: Routledge.

Caravaggio, N. (2022). Economic growth and forest transition in Latin America. Forest Policy Econ. 135:102667. doi: 10.1016/j.forpol.2021.102667

Carr, D. L., Suter, L., and Barbieri, A. (2005). Population dynamics and tropical deforestation: state of the debate and conceptual challenges. Popul. Environ. 27, 89–113. doi: 10.1007/s11111-005-0014-x

Céspedes, J., Sylvester, J. M., Pérez-Marulanda, L., Paz-Garcia, P., Reymondin, L., Khodadadi, M., et al. (2022). Has global deforestation accelerated due to the COVID-19 pandemic? J. For. Res. 34, 1153–1165. doi: 10.1007/s11676-022-01561-7

Cropper, M., and Griffiths, C. (1994). The interaction of population growth and environmental quality. Am. Econ. Rev. 84, 250–254.

Culas, R. J. (2007). Deforestation and the environmental Kuznets curve: an institutional perspective. Ecol. Econ. 61, 429–437. doi: 10.1016/j.ecolecon.2006.03.014

Curtis, P. G., Slay, C. M., Harris, N. L., Tyukavina, A., and Hansen, M. C. (2018). Classifying drivers of global forest loss. Science 361, 1108–1111. doi: 10.1126/science.aau3445

Damette, O., and Delacote, P. (2012). On the economic factors of deforestation: what can we learn from quantile analysis? Econ. Model. 29, 2427–2434. doi: 10.1016/j.econmod.2012.06.015

Derouin, S.. (2019). Deforestation: Facts, Causes & Effects. Available at: https://www.livescience.com/27692-deforestation.html (Accessed March 25, 2023).

Destiartono, M. E., and Ekananda, M. (2023). Deforestation-induced the EKC framework: the role of corruption control and trade openness in Southeast Asia. Jurnal Ekonomi & Studi Pembangunan 24, 81–99. doi: 10.18196/jesp.v24i1.16798

Ehrhardt-Martinez, K. (1998). Social determinants of deforestation in developing countries: a cross-national study. Soc. Forces 77, 567–586. doi: 10.1093/sf/77.2.567

Elliott, L. (2011). Shades of green in East Asia: the impact of financial crises on the environment. Contemp. Polit. 17, 167–183. doi: 10.1080/13569775.2011.565985

Ewers, R. M. (2006). Interaction effects between economic development and forest cover determine deforestation rates. Glob. Environ. Chang. 16, 161–169. doi: 10.1016/j.gloenvcha.2005.12.001

FAO. (2020). Global Forest Resources Assessment 2020. Available at: https://fra-data.fao.org/assessments/fra/2020 (Accessed April 4, 2023).

Ferrer Velasco, R., Köthke, M., Lippe, M., and Günter, S. (2020). Scale and context dependency of deforestation drivers: insights from spatial econometrics in the tropics. PLoS One 15:e0226830. doi: 10.1371/journal.pone.0226830

González-Eguino, M. (2015). Energy poverty: an overview. Renew. Sust. Energ. Rev. 47, 377–385. doi: 10.1016/j.rser.2015.03.013

Jallat, H., Khokhar, M. F., Kudus, K. A., Nazre, M., Saqib, N. U., Tahir, U., et al. (2021). Monitoring carbon stock and land-use change in 5000-year-old juniper forest stand of Ziarat, Balochistan, through a synergistic approach. Forests 12, 1–15. doi: 10.3390/f12010051

Jayathilake, H. M., Prescott, G. W., Carrasco, L. R., Rao, M., and Symes, W. S. (2021). Drivers of deforestation and degradation for 28 tropical conservation landscapes. Ambio 50, 215–228. doi: 10.1007/s13280-020-01325-9

Jindřichovská, I., and Uğurlu, E. (2021). EU and China trends in trade in challenging times. J. Risk Financ. Manag. 14, 1–19. doi: 10.3390/jrfm14020071

Khalid, N., Ullah, S., Ahmad, S. S., Ali, A., and Chishtie, F. (2019). A remotely sensed tracking of forest cover and associated temperature change in Margalla hills. Int. J. Digit. Earth 12, 1133–1150. doi: 10.1080/17538947.2018.1448008

Lawrence, D., Coe, M., Walker, W., Verchot, L., and Vandecar, K. (2022). The unseen effects of deforestation: biophysical effects on climate. Front. For. Glob. Change 5:49. doi: 10.3389/ffgc.2022.756115

Leisher, C., Touval, J., Hess, S. M., Boucher, T. M., and Reymondin, L. (2013). Land and forest degradation inside protected areas in Latin America. Diversity 5, 779–795. doi: 10.3390/d5040779

Ma, J., Li, J., Wu, W., and Liu, J. (2023). Global forest fragmentation change from 2000 to 2020. Nat. Commun. 14, 3752–3710. doi: 10.1038/s41467-023-39221-x

Marchand, S. (2016). The colonial origins of deforestation: an institutional analysis. Environ. Dev. Econ. 21, 318–349. doi: 10.1017/S1355770X1500025X

Maretto, R. V., Fonseca, L. M., Jacobs, N., Körting, T. S., Bendini, H. N., and Parente, L. L. (2020). Spatio-temporal deep learning approach to map deforestation in amazon rainforest. IEEE Geosci. Remote Sens. Lett. 18, 771–775. doi: 10.1109/LGRS.2020.2986407

Martínez, C. I. P., and Poveda, A. C. (2021). The importance of science, technology and innovation in the green growth and sustainable development goals of Colombia. Environ. Clim. Technol. 25, 29–41. doi: 10.2478/rtuect-2021-0003

Mather, A. S., and Needle, C. L. (2005). The relationships of population and forest trends. Geogr. J. 166, 2–13. doi: 10.1111/j.1475-4959.2000.tb00002.x

McCallister, M., Krasovskiy, A., Platov, A., Pietracci, B., Golub, A., Lubowski, R., et al. (2022). Forest protection and permanence of reduced emissions. Front. For. Glob. Change 5:928518. doi: 10.3389/ffgc.2022.928518

Miettinen, J., Stibig, H. J., and Achard, F. (2014). Remote sensing of forest degradation in Southeast Asia—aiming for a regional view through 5–30 m satellite data. Glob. Ecol. Conserv. 2, 24–36. doi: 10.1016/j.gecco.2014.07.007

Nguyen, C. P., and Nguyen, B. Q. (2023). Environmental foe or friend: the influence of the shadow economy on forest land. Land Use Policy 124:106456. doi: 10.1016/j.landusepol.2022.106456

Nguyen, C. P., Nguyen, B. Q., and Tran, D. T. L. (2023). Over two decades of severe deforestation: an economic perspective of tourism development. J. Environ. Stud. Sci. 13, 83–104. doi: 10.1007/s13412-022-00802-9

Our World in Data. (2021). Forests and Deforestation. Available at: https://ourworldindata.org/forests-and-deforestation (Accessed June 11, 2023).

Our World in Data. (2023). Coronavirus Pandemic (COVID-19). Available at: https://ourworldindata.org/coronavirus (Accessed April 22, 2023).

Oyetunji, P. O., Ibitoye, O. S., Akinyemi, G. O., Fadele, O. A., and Oyediji, O. T. (2020). The effects of population growth on deforestation in Nigeria: 1991–2016. J. Appl. Sci. Environ. Manag. 24, 1329–1334. doi: 10.4314/jasem.v24i8.4

Santos de Lima, L., Merry, F., Soares-Filho, B., Oliveira Rodrigues, H., dos Santos Damaceno, C., and Bauch, M. A. (2018). Illegal logging as a disincentive to the establishment of a sustainable forest sector in the Amazon. PLoS One 13, e0207855–e0207821. doi: 10.1371/journal.pone.0207855

Scrieciu, S. S. (2007). Can economic causes of tropical deforestation be identified at a global level? Ecol. Econ. 62, 603–612. doi: 10.1016/j.ecolecon.2006.07.028

Shafron, E. S. (2019). Examining connections between gendered dimensions of inequality and deforestation in Nepal. Available at: https://scholarworks.uvm.edu/cgi/viewcontent.cgi?article=1067&context=envstheses (Accessed May 20, 2023).

Silva Junior, C. H., Pessôa, A. C., Carvalho, N. S., Reis, J. B., Anderson, L. O., and Aragão, L. E. (2021). The Brazilian Amazon deforestation rate in 2020 is the greatest of the decade. Nat. Ecol. Evol. 5, 144–145. doi: 10.1038/s41559-020-01368-x

Stabile, M. C., Garcia, A. S., Salomão, C. S., Bush, G., Guimarães, A. L., and Moutinho, P. (2022). Slowing deforestation in the Brazilian Amazon: avoiding legal deforestation by compensating farmers and ranchers. Front. For. Glob. Change 4:635638. doi: 10.3389/ffgc.2021.635638

Strandberg, G., and Kjellström, E. (2019). Climate impacts from afforestation and deforestation in Europe. Earth Interact. 23, 1–27. doi: 10.1175/EI-D-17-0033.1

The Fact File. (2022) Landlocked Countries in the World Listed. Available at: https://thefactfile.org/landlocked-countries-list/ (Accessed March 20, 2023).

Torres-Reyna, O. (2007). Panel data analysis fixed and random effects using Stata (v. 4.2) Data & Statistical Services New Jersey: Priceton University, 112.

Uğurlu, E., and Jindřichovská, I. (2022). Effect of COVID-19 on international trade among the Visegrad countries. J. Risk Financ. Manag. 15, 1–20. doi: 10.3390/jrfm15020041

Vale, M. M., Berenguer, E., de Menezes, M. A., de Castro, E. B. V., de Siqueira, L. P., and Rita de Cássia, Q. P. (2021). The COVID-19 pandemic as an opportunity to weaken environmental protection in Brazil. Biol. Conserv. 255, 108994–108995. doi: 10.1016/j.biocon.2021.108994

Van Khuc, Q., Tran, B. Q., Meyfroidt, P., and Paschke, M. W. (2018). Drivers of deforestation and forest degradation in Vietnam: an exploratory analysis at the national level. Forest Policy Econ. 90, 128–141. doi: 10.1016/j.forpol.2018.02.004

World Bank. (2023). World Bank Open Data. Available at: https://data.worldbank.org/indicator (Accessed May 22, 2023).

Zeb, A., Hamann, A., Armstrong, G. W., and Acuna-Castellanos, D. (2019). Identifying local actors of deforestation and forest degradation in the Kalasha valleys of Pakistan. Forest Policy Econ. 104, 56–64. doi: 10.1016/j.forpol.2019.04.005

Zerriffi, H., Reyes, R., and Maloney, A. (2023). Pathways to sustainable land use and food systems in Canada. Sustain. Sci. 18, 389–406. doi: 10.1007/s11625-022-01213-z

Keywords: deforestation, afforestation, economic development, social development, forest area, GDP

Citation: Prochazka P, Abrham J, Cerveny J, Kobera L, Sanova P, Benes D, Fink J-M, Jiraskova E, Primasova S, Soukupova J and Smutka L (2023) Understanding the socio-economic causes of deforestation: a global perspective. Front. For. Glob. Change . 6:1288365. doi: 10.3389/ffgc.2023.1288365

Received: 04 September 2023; Accepted: 05 October 2023; Published: 19 October 2023.

Reviewed by:

Copyright © 2023 Prochazka, Abrham, Cerveny, Kobera, Sanova, Benes, Fink, Jiraskova, Primasova, Soukupova and Smutka. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Josef Abrham, [email protected]

--> AGU