Assignment Problem: Meaning, Methods and Variations | Operations Research
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.
The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.
Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.
Definition of Assignment Problem:
ADVERTISEMENTS:
Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.
The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:
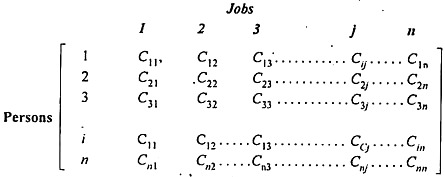
- Google OR-Tools
- Español – América Latina
- Português – Brasil
- Tiếng Việt
Solving an Assignment Problem
This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.
In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .
The costs of assigning workers to tasks are shown in the following table.
The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.
MIP solution
The following sections describe how to solve the problem using the MPSolver wrapper .
Import the libraries
The following code imports the required libraries.
Create the data
The following code creates the data for the problem.
The costs array corresponds to the table of costs for assigning workers to tasks, shown above.
Declare the MIP solver
The following code declares the MIP solver.
Create the variables
The following code creates binary integer variables for the problem.
Create the constraints
Create the objective function.
The following code creates the objective function for the problem.
The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.
Invoke the solver
The following code invokes the solver.
Print the solution
The following code prints the solution to the problem.
Here is the output of the program.
Complete programs
Here are the complete programs for the MIP solution.
CP SAT solution
The following sections describe how to solve the problem using the CP-SAT solver.
Declare the model
The following code declares the CP-SAT model.
The following code sets up the data for the problem.
The following code creates the constraints for the problem.
Here are the complete programs for the CP-SAT solution.
Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.
Last updated 2023-01-02 UTC.
- Data Structures
- Linked List
- Binary Tree
- Binary Search Tree
- Segment Tree
- Disjoint Set Union
- Fenwick Tree
- Red-Black Tree
- Advanced Data Structures
Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)
- Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
- Introduction to Exact Cover Problem and Algorithm X
- Greedy Approximate Algorithm for Set Cover Problem
- Job Assignment Problem using Branch And Bound
- Implementation of Exhaustive Search Algorithm for Set Packing
- Channel Assignment Problem
- Chocolate Distribution Problem | Set 2
- Transportation Problem | Set 1 (Introduction)
- OLA Interview Experience | Set 11 ( For Internship)
- Top 20 Greedy Algorithms Interview Questions
- Job Sequencing Problem - Loss Minimization
- Prim's Algorithm (Simple Implementation for Adjacency Matrix Representation)
- Data Structures and Algorithms | Set 21
- Adobe Interview Experience | Set 55 (On-Campus Full Time for MTS profile)
- Amazon Interview Experience | Set 211 (On-Campus for Internship)
- OYO Rooms Interview Experience | Set 3 (For SDE-II, Gurgaon)
- C# Program for Dijkstra's shortest path algorithm | Greedy Algo-7
- Algorithms | Dynamic Programming | Question 7
- Amazon Interview | Set 46 (On-campus for Internship)
- For each row of the matrix, find the smallest element and subtract it from every element in its row.
- Do the same (as step 1) for all columns.
- Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
- Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
- Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
Try it before moving to see the solution
Explanation for above simple example:
An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.
Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).
Space complexity : O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.
In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY
Please Login to comment...
Similar reads.
- Mathematical
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
A Comparative Analysis of Assignment Problem
- Conference paper
- First Online: 06 June 2023
- Cite this conference paper

- Shahriar Tanvir Alam ORCID: orcid.org/0000-0002-0567-3381 5 ,
- Eshfar Sagor 5 ,
- Tanjeel Ahmed 5 ,
- Tabassum Haque 5 ,
- Md Shoaib Mahmud 5 ,
- Salman Ibrahim 5 ,
- Ononya Shahjahan 5 &
- Mubtasim Rubaet 5
Part of the book series: EAI/Springer Innovations in Communication and Computing ((EAISICC))
Included in the following conference series:
- International Conference on Big Data Innovation for Sustainable Cognitive Computing
121 Accesses
The aim of a supply chain team is to formulate a network layout that minimizes the total cost. In this research, the lowest production cost of the final product has been determined using a generalized plant location model. Furthermore, it is anticipated that units have been set up appropriately so that one unit of input from a source of supply results in one unit of output. The assignment problem is equivalent to distributing a job to the appropriate machine in order to meet customer demand. This study concentrates on reducing the cost of fulfilling the overall customer demand. Many studies have been conducted, and various algorithms have been proposed to achieve the best possible result. The purpose of this study is to present an appropriate model for exploring the solution to the assignment problem using the “Hungarian Method.” To find a feasible output of the assignment problem, this study conducted a detailed case study. The computational results indicate that the “Hungarian Method” provides an optimum solution for both balanced and unbalanced assignment problems. Moreover, decision-makers can use the study’s findings as a reference to mitigate production costs and adopt any sustainable market policy.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Durable hardcover edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Z. Xiang, J. Yang, X. Liang, M.H. Naseem, Application of discrete Grey Wolf Algorithm in balanced transport problem, in 2021 3rd International Academic Exchange Conference on Science and Technology Innovation, IAECST 2021 , (2021), pp. 1312–1318. https://doi.org/10.1109/IAECST54258.2021.9695827
Chapter Google Scholar
C. Woodyard, New York City Is Costliest Place to Park in USA (2018). https://content.usatoday.com/communities/driveon/post/2011/07/new-york-city-costliest-place-to-park-your-car/1#.WWUoFoQrJdg . Accessed 23 Apr 2022
K. McCoy, Drivers spend an average of 17 hours a year searching for parking spots. USA Today (2017). https://www.usatoday.com/story/money/2017/07/12/parking-pain-causes-financial-and-personal-strain/467637001/ . Accessed 23 Apr 2022
W. Ho, P. Ji, A genetic algorithm for the generalised transportation problem. Int. J. Comput. Appl. Technol. 22 (4), 190–197 (2005). https://doi.org/10.1504/IJCAT.2005.006959
Article Google Scholar
Z. Nakat, S. Herrera, Y. Cherkaoui, Cairo Traffic Congestion Study (World Bank, Washington, DC, 2013)
Google Scholar
S. Bussmann, K. Schild, An agent-based approach to the control of flexible production systems, in IEEE International Conference on Emerging Technologies and Factory Automation, ETFA , vol. 2, (2001), pp. 481–488. https://doi.org/10.1109/etfa.2001.997722
S. Emde, M. Gendreau, Scheduling in-house transport vehicles to feed parts to automotive assembly lines. Eur. J. Oper. Res. 260 (1), 255–267 (2017). https://doi.org/10.1016/j.ejor.2016.12.012
Article MathSciNet MATH Google Scholar
S. Chopra, G. Notarstefano, M. Rice, M. Egerstedt, A distributed version of the Hungarian method for multirobot assignment. IEEE Trans. Robot. 33 (4), 932–947 (2017). https://doi.org/10.1109/TRO.2017.2693377
H.A. Hussein, M.A.K. Shiker, Two new effective methods to find the optimal solution for the assignment problems. J. Adv. Res. Dyn. Control Syst. 12 (7), 49–54 (2020). https://doi.org/10.5373/JARDCS/V12I7/20201983
M. Chen, D. Zhu, A workload balanced algorithm for task assignment and path planning of inhomogeneous autonomous underwater vehicle system. IEEE Trans. Cogn. Develop. Syst. 11 (4), 483–493 (2018)
C. Cubukcuoglu, P. Nourian, M.F. Tasgetiren, I.S. Sariyildiz, S. Azadi, Hospital layout design renovation as a quadratic assignment problem with geodesic distances. J. Build. Eng. 44 , 102952 (2021). https://doi.org/10.1016/j.jobe.2021.102952
U. Tosun, A new tool for automated transformation of quadratic assignment problem instances to quadratic unconstrained binary optimisation models. Expert Syst. Appl. 201 , 116953 (2022). https://doi.org/10.1016/j.eswa.2022.116953
S.M. Homayouni, D.B.M.M. Fontes, Production and transport scheduling in flexible job shop manufacturing systems. J. Glob. Optim. 79 (2), 463–502 (2021). https://doi.org/10.1007/s10898-021-00992-6
Article MathSciNet Google Scholar
R. Wang, J. Yan, X. Yang, Neural graph matching network: Learning Lawler’s quadratic assignment problem with extension to hypergraph and multiple-graph matching. IEEE Trans. Pattern Anal. Mach. Intell. 44 (9), 5261–5279 (2022). https://doi.org/10.1109/TPAMI.2021.3078053
T. Dokeroglu, E. Sevinc, A. Cosar, Artificial bee colony optimization for the quadratic assignment problem. Appl. Soft Comput. J. 76 , 595–606 (2019). https://doi.org/10.1016/j.asoc.2019.01.001
X. Xiang, C. Liu, An almost robust optimization model for integrated berth allocation and quay crane assignment problem. Omega (United Kingdom) 104 , 102455 (2021). https://doi.org/10.1016/j.omega.2021.102455
Ö. Karsu, M. Azizoğlu, K. Alanlı, Exact and heuristic solution approaches for the airport gate assignment problem. Omega (United Kingdom) 103 , 102422 (2021). https://doi.org/10.1016/j.omega.2021.102422
A.S. Hameed, M.L. Mutar, H.M.B. Alrikabi, Z.H. Ahmed, A.A. Abdul-Razaq, H.K. Nasser, A hybrid method integrating a discrete differential evolution algorithm with tabu search algorithm for the quadratic assignment problem: A new approach for locating hospital departments. Math. Probl. Eng. 2021 (2021). https://doi.org/10.1155/2021/6653056
S.T. Ngo, J. Jaafar, I.A. Aziz, B.N. Anh, A compromise programming for multi-objective task assignment problem. Computers 10 (2), 1–16 (2021). https://doi.org/10.3390/computers10020015
X. Zheng, D. Zhou, N. Li, T. Wu, Y. Lei, J. Shi, Self-adaptive multi-task differential evolution optimization: With case studies in weapon–target assignment problem. Electronics 10 (23), 2945 (2021). https://doi.org/10.3390/electronics10232945
X. Hu, C. Liang, D. Chang, Y. Zhang, Container storage space assignment problem in two terminals with the consideration of yard sharing. Adv. Eng. Inform. 47 , 101224 (2021). https://doi.org/10.1016/j.aei.2020.101224
Q. Rabbani, A. Khan, A. Quddoos, Modified Hungarian method for unbalanced assignment problem with multiple jobs. Appl. Math. Comput. 361 , 493–498 (2019). https://doi.org/10.1016/j.amc.2019.05.041
A. Kumar, A modified method for solving the unbalanced assignment problems. Appl. Math. Comput. 176 (1), 76–82 (2006). https://doi.org/10.1016/j.amc.2005.09.056
A. Iampang, V. Boonjing, P. Chanvarasuth, A cost and space efficient method for unbalanced assignment problems, in IEEM2010 – IEEE International Conference on Industrial Engineering and Engineering Management , (2010), pp. 985–988. https://doi.org/10.1109/IEEM.2010.5674228
L. Wang, Z. He, C. Liu, Q. Chen, Graph based twin cost matrices for unbalanced assignment problem with improved ant colony algorithm. Results Appl. Math. 12 , 100207 (2021). https://doi.org/10.1016/j.rinam.2021.100207
Download references
Author information
Authors and affiliations.
Military Institute of Science and Technology, Department of Industrial and Production Engineering, Dhaka, Bangladesh
Shahriar Tanvir Alam, Eshfar Sagor, Tanjeel Ahmed, Tabassum Haque, Md Shoaib Mahmud, Salman Ibrahim, Ononya Shahjahan & Mubtasim Rubaet
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Shahriar Tanvir Alam .
Editor information
Editors and affiliations.
Department of Computer Science and Engineering, Sri Eshwar College of Engineering, Coimbatore, Tamil Nadu, India
Anandakumar Haldorai
Department of Computer Science and Engineering, CMR University, Bengaluru, Karnataka, India
Arulmurugan Ramu
Sri Eshwar College of Engineering, Coimbatore, Tamil Nadu, India
Sudha Mohanram
Rights and permissions
Reprints and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper.
Alam, S.T. et al. (2023). A Comparative Analysis of Assignment Problem. In: Haldorai, A., Ramu, A., Mohanram, S. (eds) 5th EAI International Conference on Big Data Innovation for Sustainable Cognitive Computing. BDCC 2022. EAI/Springer Innovations in Communication and Computing. Springer, Cham. https://doi.org/10.1007/978-3-031-28324-6_11
Download citation
DOI : https://doi.org/10.1007/978-3-031-28324-6_11
Published : 06 June 2023
Publisher Name : Springer, Cham
Print ISBN : 978-3-031-28323-9
Online ISBN : 978-3-031-28324-6
eBook Packages : Engineering Engineering (R0)
Share this paper
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
Hungarian Method
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.
Hungarian Method to Solve Assignment Problems
The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.
What is an Assignment Problem?
A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.
Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.
Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps
Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.
Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.
Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.
Step 3 – Assign zeros
- Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
- Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.
Step 4 – Perform the Optimal Test
- The present assignment is optimal if each row and column has exactly one encircled zero.
- The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.
Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:
(a) Highlight the rows that aren’t assigned.
(b) Label the columns with zeros in marked rows (if they haven’t already been marked).
(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).
(d) Continue with (b) and (c) until no further marking is needed.
(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.
Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.
Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.
Hungarian Method Example
Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.
\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
With 5 jobs and 5 men, the stated problem is balanced.
\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)
Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)
When the zeros are assigned, we get the following:
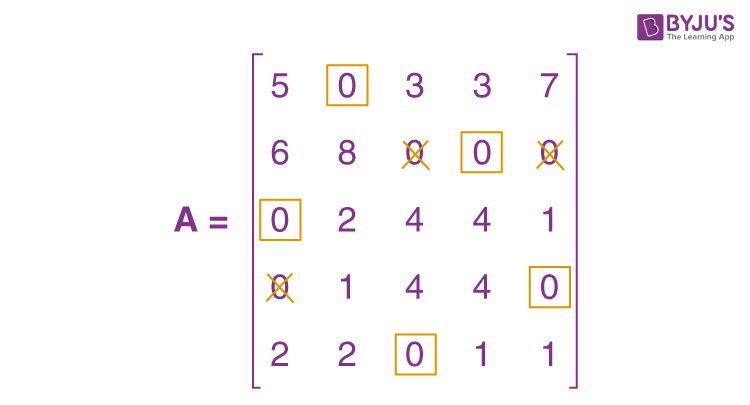
The present assignment is optimal because each row and column contain precisely one encircled zero.
Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.
Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.
Practice Question on Hungarian Method
Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.
\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)
Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.
Frequently Asked Questions on Hungarian Method
What is hungarian method.
The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.
What are the steps involved in Hungarian method?
The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.
What is the purpose of the Hungarian method?
When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
- Share Share
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.


Unbalanced Assignment Problem: Definition, Formulation, and Solution Methods
Table of Contents
Are you familiar with the assignment problem in Operations Research (OR)? This problem deals with assigning tasks to workers in a way that minimizes the total cost or time needed to complete the tasks. But what if the number of tasks and workers is not equal? In this case, we face the Unbalanced Assignment Problem (UAP). This blog will help you understand what the UAP is, how to formulate it, and how to solve it.
What is the Unbalanced Assignment Problem?
The Unbalanced Assignment Problem is an extension of the Assignment Problem in OR, where the number of tasks and workers is not equal. In the UAP, some tasks may remain unassigned, while some workers may not be assigned any task. The objective is still to minimize the total cost or time required to complete the assigned tasks, but the UAP has additional constraints that make it more complex than the traditional assignment problem.
Formulation of the Unbalanced Assignment Problem
To formulate the UAP, we start with a matrix that represents the cost or time required to assign each task to each worker. If the matrix is square, we can use the Hungarian algorithm to solve the problem. But when the matrix is not square, we need to add dummy tasks or workers to balance the matrix. These dummy tasks or workers have zero costs and are used to make the matrix square.
Once we have a square matrix, we can apply the Hungarian algorithm to find the optimal assignment. However, we need to be careful in interpreting the results, as the assignment may include dummy tasks or workers that are not actually assigned to anything.
Solutions for the Unbalanced Assignment Problem
Besides the Hungarian algorithm, there are other methods to solve the UAP, such as the transportation algorithm and the auction algorithm. The transportation algorithm is based on transforming the UAP into a transportation problem, which can be solved with the transportation simplex method. The auction algorithm is an iterative method that simulates a bidding process between the tasks and workers to find the optimal assignment.
In summary, the Unbalanced Assignment Problem is a variant of the traditional Assignment Problem in OR that deals with assigning tasks to workers when the number of tasks and workers is not equal. To solve the UAP, we need to balance the matrix by adding dummy tasks or workers and then apply algorithms such as the Hungarian algorithm, the transportation algorithm, or the auction algorithm. Understanding the UAP can help businesses and organizations optimize their resource allocation and improve their operational efficiency.
How useful was this post?
Click on a star to rate it!
Average rating 1 / 5. Vote count: 1
No votes so far! Be the first to rate this post.
We are sorry that this post was not useful for you! 😔
Let us improve this post!
Tell us how we can improve this post?
Operations Research
1 Operations Research-An Overview
- History of O.R.
- Approach, Techniques and Tools
- Phases and Processes of O.R. Study
- Typical Applications of O.R
- Limitations of Operations Research
- Models in Operations Research
- O.R. in real world
2 Linear Programming: Formulation and Graphical Method
- General formulation of Linear Programming Problem
- Optimisation Models
- Basics of Graphic Method
- Important steps to draw graph
- Multiple, Unbounded Solution and Infeasible Problems
- Solving Linear Programming Graphically Using Computer
- Application of Linear Programming in Business and Industry
3 Linear Programming-Simplex Method
- Principle of Simplex Method
- Computational aspect of Simplex Method
- Simplex Method with several Decision Variables
- Two Phase and M-method
- Multiple Solution, Unbounded Solution and Infeasible Problem
- Sensitivity Analysis
- Dual Linear Programming Problem
4 Transportation Problem
- Basic Feasible Solution of a Transportation Problem
- Modified Distribution Method
- Stepping Stone Method
- Unbalanced Transportation Problem
- Degenerate Transportation Problem
- Transhipment Problem
- Maximisation in a Transportation Problem
5 Assignment Problem
- Solution of the Assignment Problem
- Unbalanced Assignment Problem
- Problem with some Infeasible Assignments
- Maximisation in an Assignment Problem
- Crew Assignment Problem
6 Application of Excel Solver to Solve LPP
- Building Excel model for solving LP: An Illustrative Example
7 Goal Programming
- Concepts of goal programming
- Goal programming model formulation
- Graphical method of goal programming
- The simplex method of goal programming
- Using Excel Solver to Solve Goal Programming Models
- Application areas of goal programming
8 Integer Programming
- Some Integer Programming Formulation Techniques
- Binary Representation of General Integer Variables
- Unimodularity
- Cutting Plane Method
- Branch and Bound Method
- Solver Solution
9 Dynamic Programming
- Dynamic Programming Methodology: An Example
- Definitions and Notations
- Dynamic Programming Applications
10 Non-Linear Programming
- Solution of a Non-linear Programming Problem
- Convex and Concave Functions
- Kuhn-Tucker Conditions for Constrained Optimisation
- Quadratic Programming
- Separable Programming
- NLP Models with Solver
11 Introduction to game theory and its Applications
- Important terms in Game Theory
- Saddle points
- Mixed strategies: Games without saddle points
- 2 x n games
- Exploiting an opponent’s mistakes
12 Monte Carlo Simulation
- Reasons for using simulation
- Monte Carlo simulation
- Limitations of simulation
- Steps in the simulation process
- Some practical applications of simulation
- Two typical examples of hand-computed simulation
- Computer simulation
13 Queueing Models
- Characteristics of a queueing model
- Notations and Symbols
- Statistical methods in queueing
- The M/M/I System
- The M/M/C System
- The M/Ek/I System
- Decision problems in queueing
Quantitative Techniques: Theory and Problems by P. C. Tulsian, Vishal Pandey
Get full access to Quantitative Techniques: Theory and Problems and 60K+ other titles, with a free 10-day trial of O'Reilly.
There are also live events, courses curated by job role, and more.
WHAT IS ASSIGNMENT PROBLEM
Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons.
The assignment problem in the general form can be stated as follows:
“Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to assign each facility to one and only one job in such a way that the measure of effectiveness is optimised (Maximised or Minimised).”
Several problems of management has a structure identical with the assignment problem.
Example I A manager has four persons (i.e. facilities) available for four separate jobs (i.e. jobs) and the cost of assigning (i.e. effectiveness) each job to each ...
Get Quantitative Techniques: Theory and Problems now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
Don’t leave empty-handed
Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.
It’s yours, free.

Check it out now on O’Reilly
Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Quadratic assignment problem
Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)
- 1 Introduction
- 2.1 Koopmans-Beckman Mathematical Formulation
- 2.2.1 Parameters
- 2.3.1 Optimization Problem
- 2.4 Computational Complexity
- 2.5 Algorithmic Discussions
- 2.6 Branch and Bound Procedures
- 2.7 Linearizations
- 3.1 QAP with 3 Facilities
- 4.1 Inter-plant Transportation Problem
- 4.2 The Backboard Wiring Problem
- 4.3 Hospital Layout
- 4.4 Exam Scheduling System
- 5 Conclusion
- 6 References
Introduction
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.
Theory, Methodology, and/or Algorithmic Discussions
Koopmans-beckman mathematical formulation.
Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.
Quadratic Assignment Problem Formulation

Inner Product

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.
Optimization Problem
With all of this information, the QAP can be summarized as:

Computational Complexity
QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]
Algorithmic Discussions
While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:
- Dynamic Program
- Cutting Plane
Branch and Bound Procedures
The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.
The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.
A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.
Linearizations
The first attempts to solve the QAP eliminated the quadratic term in the objective function of

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.
Numerical Example
Qap with 3 facilities.

Applications
Inter-plant transportation problem.
The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.
The Backboard Wiring Problem
As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]
When defining the problem Steinberg states that we have a set of n elements

as well as a set of r points

In his paper he derives the below formula:

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.
The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.
Hospital Layout
Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.
Elshafei identified the following QAP to determine where clinics should be placed:

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.
Exam Scheduling System
The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

- ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
- ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
- ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
- ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
- ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
- ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.
Navigation menu

IMAGES
VIDEO
COMMENTS
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations. Meaning of Assignment Problem: An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total ...
Worked example of assigning tasks to an unequal number of workers using the Hungarian method. The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: The problem instance has a number of agents and a number of tasks.Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent ...
Step 1: Set up the cost matrix. The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in ... , the more suitable the candidate is for that ... (give jobs to as many men as possible) for which the sum of the cost of the edges is minimized. Naive solution In the previous lecture, we have learned
This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver. Example. In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview.
The Assignment Problem: An Example A company has 4 machines available for assignment to 4 tasks. Any machine can be assigned to any task, and each task requires processing by one machine. The time required to set up each machine for the processing of each task is given in the table below. TIME (Hours) Task 1 Task 2 Task 3 Task 4 Machine 1 13 4 7 6
Small example just to make things clearer: General description of the algorithm. This problem is known as the assignment problem. The assignment problem is a special case of the transportation problem, which in turn is a special case of the min-cost flow problem, so it can be solved using algorithms that solve the more general cases. Also, our ...
Step 3. Cover all the zeros of the matrix with the minimum number of horizontal or vertical lines. Step 4. Since the minimal number of lines is 3, an optimal assignment of zeros is possible and we are finished. Since the total cost for this assignment is 0, it must be. Step 3.
5.1 INTRODUCTION. The assignment problem is one of the special type of transportation problem for which more efficient (less-time consuming) solution method has been devised by KUHN (1956) and FLOOD (1956). The justification of the steps leading to the solution is based on theorems proved by Hungarian mathematicians KONEIG (1950) and EGERVARY ...
First, we give a detailed review of two algorithms that solve the minimization case of the assignment problem, the Bertsekas auction algorithm and the Goldberg & Kennedy algorithm. It was previously alluded that both algorithms are equivalent. We give a detailed proof that these algorithms are equivalent. Also, we perform experimental results comparing the performance of three algorithms for ...
8.1 Introduction. An assignment problem is a particular case of transportation problem in which a number of operations are to be assigned to an equal number of operators, where each operator performs only one operation. The objective is to minimize overall cost or to maximize the overall profit for a given assignment schedule.
For example, the problem could be one of matching jobs with workers and machines or one of assigning students and teachers to classes and time slots. (There is a considerable body of literature on the. Summary. Assignment problems involve matching the elements of two or more sets in such a way that some objective function is optimized.
Example 4 In the job assignment problem described in Example 1 of the Introduction, there are 3! = 6 permutations: σ1 = 123 cost:31 σ4 = 312 cost:36 σ2 = 132 cost:30 σ5 = 231 cost:34 σ3 = 213 cost:37 σ6 = 321 cost:34. Thus, σ2 solves the problem and indicates that the best assignment is to assign worker 1 to job 1, worker 2 to job 3, and ...
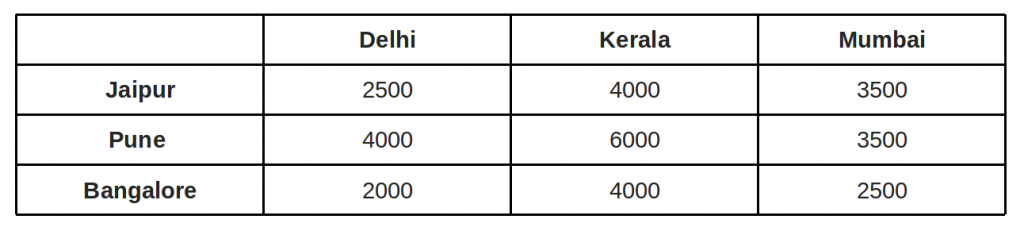
Explanation for above simple example: Below is the cost matrix of example given in above diagrams. 2500 4000 3500 4000 6000 3500 2000 4000 2500 Step 1: Subtract minimum of every row. 2500, 3500 and 2000 are subtracted from rows 1, 2 and 3 respectively. 0 1500 1000 500 2500 0 0 2000 500 Step 2: Subtract minimum of every column. 0, 1500 and 0 are subtracted from columns 1, 2 and 3 respectively.
Tables 2, 3, 4, and 5 present the steps required to determine the appropriate job assignment to the machine. Step 1 By taking the minimum element and subtracting it from all the other elements in each row, the new table will be: Table 2 represents the matrix after completing the 1st step. Table 1 Initial table of a.
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term "Hungarian method" to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let's go through the steps of the Hungarian method with the help of a solved example.
The Unbalanced Assignment Problem is an extension of the Assignment Problem in OR, where the number of tasks and workers is not equal. In the UAP, some tasks may remain unassigned, while some workers may not be assigned any task. The objective is still to minimize the total cost or time required to complete the assigned tasks, but the UAP has ...
3. Do the same for some variants of transportation problems. 4. Give the name of two algorithms that can solve huge transportation problems that are well beyond the scope of Solver. 5. Identify several areas of application of transportation problems and their variants. 6. Describe the characteristics of assignment problems. 7.
Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons. The assignment problem in the general form can be stated as follows: "Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to ...
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957, is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. ... As an example, the permutation ...
Within the education domain, this review classified the assignment problem into two: timetabling problem and allocation problem. Assignment problem refers to the analysis on how to assign objects to objects in the best possible way (optimal way) [ 2, 3 ]. The two components of assignment problem are the assignments and the objective function.
How to Define a Research Problem | Ideas & Examples. Published on November 2, 2022 by Shona McCombes and Tegan George. Revised on May 31, 2023. A research problem is a specific issue or gap in existing knowledge that you aim to address in your research. You may choose to look for practical problems aimed at contributing to change, or theoretical problems aimed at expanding knowledge.
The timetabling problem is further classified into examination, course, and school timetabling problems, while the allocation problem is divided into student-project allocation, new student ...