trigonometry questions height and distance

Heights and Distances

In this topic, we will be studying some ways in which trigonometry is used in life around you.

What is meant by trigonometry?

Trigonometry is one of the most ancient subjects studied by scholars all over the world. Trigonometry was invented because its need arose in astronomy . Since then astronomers have used it, for instance, to calculate distances from the Earth to the planets and stars. Trigonometry is also used in geography and in navigation .

The knowledge of trigonometry is used to find heights of structures, construct maps, determine the position of an island in relation to the longitudes and latitudes.

Lesson Plan

What do you mean by height and distances.

The most significant definitions that are used when dealing with heights and distances are given as:

Line of sight:  It is the line drawn from the eye of an observer to the point in the object viewed by the observer.

Here, the cat is the observer and the object is the bird.

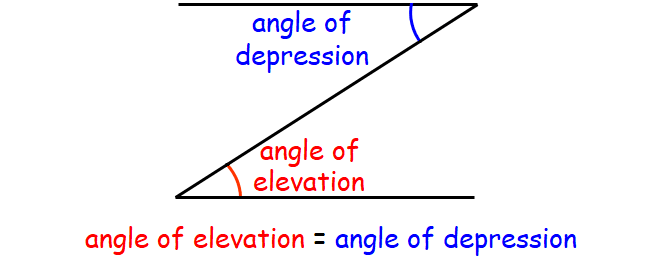
The angle of elevation: The angle between the horizontal and the line of sight joining an observation point to an elevated object.

In the following figure, the angle of elevation of the kite from the point \(A\) is \({30^\circ }\), and from point \(B\) is \({60^\circ }\)

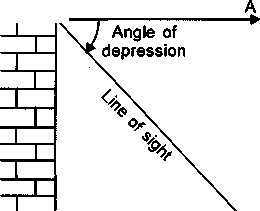
The angle of depression: The angle between the horizontal and the line of sight joining an observation point to an object below the horizontal level.

In the following figure, if the top of the building is our observation point, then the angle of depression of person \(X\) is \({45^\circ}\), and that of person \(Y\)  is \({60^\circ }\).

Let us now experience how trigonometry is applied to practical situations.

What Are the Formulas for Heights and Distances?

Trigonometric ratios can be used to find heights and distances. Some useful relations are illustrated by the below-given diagrams which help us to determine heights and distances.

The angles of depression of the top and the bottom of an \(8\, yd\) tall building from the top of a multi-storeyed building are \(30^\circ \) and \(45^\circ \), respectively. Find the height of the multi-storeyed building and the distance between the two buildings.

Hint: Try to depict the figure according to a given situation.

How to Find Height and Distances?

To measure the heights and distances of different objects, we use trigonometric ratios. 

Use the Tangent rule to calculate the height of the tree (above eye level). tan(angle) = opposite/adjacent Where the opposite is the height of the tree and adjacent is the distance between you and the tree.

This is rearranged to: opposite = tan(angle) x adjacent

or more simply \[\text{height} = \text{tan(angle)} \times \text{distance}\]

Distance can be calculated as:

\(\text{B (distance)} = \dfrac {\text{A (height)}} {\text{tan (e)}}\)

Therefore, to calculate \(B\) (distance) we will need the value of \(A\) (height) and angle \(e\).

1. The angle between the horizontal and the line of sight joining an observation point to an object below the horizontal level is called the angle of elevation.

2. The angle between the horizontal and the line of sight joining an observation point to an object below the horizontal level is called the angle of depression.

3. \(\text{B (distance)} = \dfrac {\text{A (height)}} {\text{tan (e)}}\)

Trigonometric Ratios Table

Values of trigonometric functions for the standard angles such as 0°, 30°, 45°, 60°, and 90° could be easily found using a trigonometric ratios table. 

The table consists of trigonometric ratios – sine, cosine, tangent, cosecant, secant, and cotangent. 

In short, these ratios are written as sin, cos, tan, cosec, sec, and cot.

It is best to remember the values of the trigonometric ratios of these standard angles.

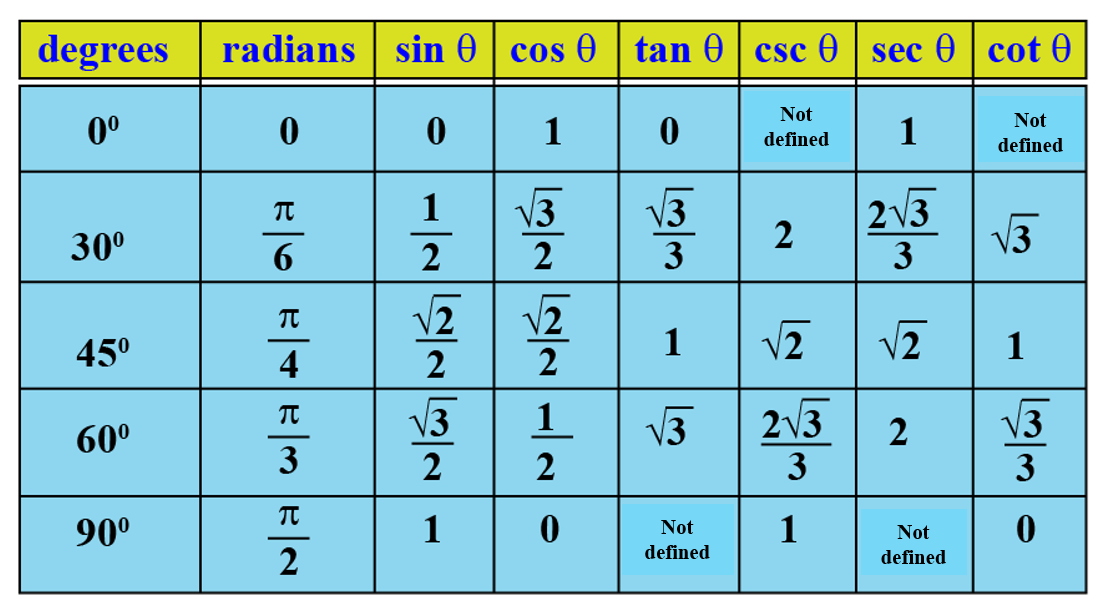
A trigonometric table has wide application in fields like science and engineering.

Solved Examples

A man standing at a certain distance from a building, observe the angle of elevation of its top to be \({60^\circ }\). He walks 30 yds away from the building. Now, the angle of elevation of the building’s top is \({30^\circ}\). How high is the building?

Let the height of the building be \(h\), and \(d\) be the original distance between the man and the building. The following figure depicts the given situation:

\[\begin{align}   \tan {60^\circ } &= \sqrt 3  \hfill \\    \Rightarrow \frac{h}{d} &= \sqrt 3  \hfill \\    \Rightarrow d &= \frac{h}{{\sqrt 3 }} \hfill \\  \end{align} \]

\[\begin{align}   \tan {30^\circ } &= \frac{1}{{\sqrt 3 }} \hfill \\    \Rightarrow \frac{h}{{d + 30}} &= \frac{1}{{\sqrt 3 }} \hfill \\    \Rightarrow \sqrt 3 h &= d + 30 \hfill \\    \Rightarrow \sqrt 3 h &= \frac{h}{{\sqrt 3 }} + 30 \hfill \\    \Rightarrow h\left( {\sqrt 3  - \frac{1}{{\sqrt 3 }}} \right) &= 30 \hfill \\  \end{align} \]

\[ \Rightarrow h = 15\sqrt 3 yd \approx 26\;yd\]

From a certain point on the ground, the angle of elevation of the top of a tree is \(\alpha \). On moving \(p\)  meters towards the tree, the angle of elevation becomes \(\beta \) . Show that the height of the tower is

\[h = \left( {\frac{{p\tan \alpha \tan \beta }}{{\tan \beta - \tan \alpha }}} \right)\;metres\]

Observe the following figure, which depicts this situation:

Here, \(d\) and \(h\)  are unknown and we need to find \(h\) .We have :

\[\tan \beta = \frac{h}{d} \Rightarrow d = h\cot \beta \]

Now, we have,

\[\begin{align}   \tan \alpha  &= \frac{h}{{p + d}} \hfill \\    \Rightarrow h &= (p + d)\tan \alpha  \hfill \\    &= (p + h\cot \beta )\tan \alpha  \hfill \\    &= p\tan \alpha  + h\tan \alpha \cot \beta  \hfill \\    \Rightarrow h\left( {1 - \tan \alpha \cot \beta } \right) &= p\tan \alpha  \hfill \\    \Rightarrow h &= \frac{{p\tan \alpha }}{{1 - \tan \alpha \cot \beta }} \hfill \\    &= \frac{{p\tan \alpha }}{{1 - \frac{{\tan \alpha }}{{\tan \beta }}}} \hfill \\  \end{align} \]

\[ h = \dfrac{p\tan \alpha \tan \beta }{\tan \beta  - \tan \alpha }\]

A house has a window \(h\) yards above the ground. Across the street from this house, there is a tall pole. The angle of elevation and depression of the top and bottom of this pole from the window are \(\theta \) and \(\varphi \) respectively. Determine the height of the pole.

The following figure depicts the given situation:

Note that \(d = h\cot \varphi \) and

\[{h_1} = d\tan \theta = h\tan \theta \cot \varphi \]

Thus, the height of the pole is,

\[\begin{gathered}   H = h + {h_1} \hfill \\    \Rightarrow H = h(1 + \tan \theta \cot \varphi ) \hfill \\  \end{gathered} \]

From an observation tower, the angle of depression of two cars on the opposite side of the tower are \(\alpha \)and \(\beta \). If the tower’s height is \(h\) yards, find the distance between the cars.

Observe the following figure:

\[d_1 = h\cot \alpha, \quad d_2 =h\cot \beta\]

Thus, the distance between the cars is,

\[D = {d_1} + {d_2} = h\left( {\cot \alpha + \cot \beta } \right)\,yd\]

I nteractive Questions

Here are a few activities for you to practice. Select/Type your answer and click the "Check Answer" button to see the result.

Let's Summarize

This mini-lesson targeted the fascinating concept of heights and distances. The math journey around the heights and distances starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Done in a way that not only it is relatable and easy to grasp, but also will stay with them forever. Here lies the magic with Cuemath.

About Cuemath

At  Cuemath , our team of math experts is dedicated to making learning fun for our favorite readers, the students!

Through an interactive and engaging learning-teaching-learning approach, the teachers explore all angles of a topic.

Be it problems, online classes, doubt sessions, or any other form of relation, it’s the logical thinking and smart learning approach that we, at Cuemath, believe in.

Frequently Asked Questions

1. how do you find the distance in trigonometry.

Therefore, to calculate \(B\) (distance) we will need the value of \(A\) (height) and angle \(e\). 

2. What is an angle of depression in trigonometry?

If a person stands and looks down at an object, the angle of depression is the angle between the horizontal line of sight and the object.

3. What is the formula for the angle of depression?

4. is the angle of elevation equal to depression.

An angle of elevation of one location relative to another is always congruent (equal in measure) to the angle of depression of the first location relative to the second.

5. What is the angle of sight in trigonometry?

The angle of elevation of an object as seen by an observer is the angle between the horizontal and the line from the object to the observer's eye (the line of sight).

6. What is the relationship between height and distance?

Using trigonometry, if we are provided with any of the two quantities that may be a side or an angle, we can calculate all the rest of the quantities. By the law of alternate angles, the angle of elevation and angle of depression are consequently equal in magnitude (α = β). Tan α is equal to the ratio of the height and distance.

7. What type of triangle is used to calculate heights and distances?

A right-angled triangle is used to calculate heights and distances.

8. What is the angle of elevation example?

• Live one on one classroom and doubt clearing
• Practice worksheets in and after class for conceptual clarity
• Personalized curriculum to keep up with school

HEIGHT AND DISTANCE PROBLEMS IN TRIGONOMETRY

To know how to solve height and distance problems in trigonometry, we must be knowing the following basic stuff in trigonometry. 

Angle of Elevation and Angle of Depression

Trigonometric Ratios

sin θ = opp/hyp

cos θ = adj/hyp

tan θ = opp/adj

opp ----> opposite side

hyp ----> hypotenuse

adj ----> adjacent side

Trigonometric ratios of angles 0°, 30°, 45°, 60° and 90°.

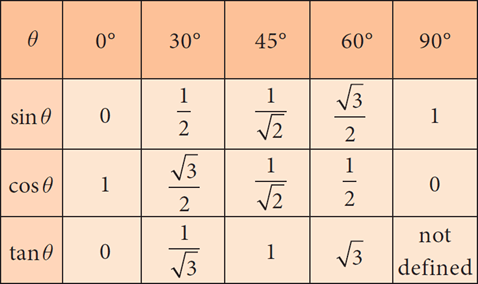
Practice Problems

Problem 1 : 

The angle of elevation of the top of the building at a distance of 50 m from its foot on a horizontal plane is found to be 60 ° . Find the height of the building.

Draw a sketch.

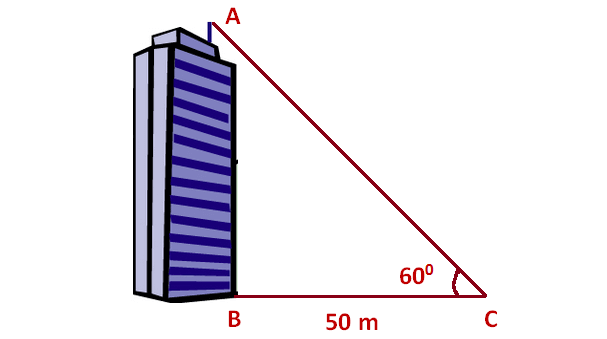
Here, AB represents height of the building, BC represents distance of the building from the point of observation.

In the right triangle ABC, the side which is opposite to the angle 60 °  is known as opposite side (AB), the side which is opposite to 90 °  is called hypotenuse side (AC) and the remaining side is called adjacent side (BC).

Now we need to find the length of the side AB.

Multiply both sides by 50.

Approximate value of √3 is 1.732.

AB  50(1.732)

     AB  ≈ 86.6

So, the height of the building is about 86.6 m.

Problem 2 :

A ladder placed against a wall such that it reaches the top of the wall of height 6 m and the ladder is inclined at an angle of 60 ° . Find how far the ladder is from the foot of the wall.

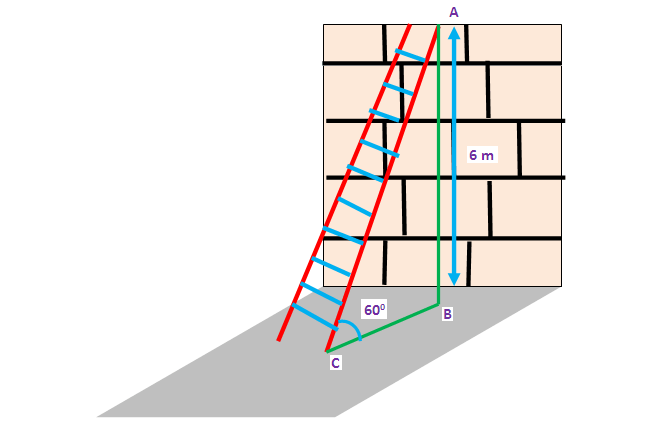
Here AB represents height of the wall, BC represents the distance between the wall and the foot of the ladder and AC represents the length of the ladder.

In the right triangle ABC, the side which is opposite to angle 60 °  is known as opposite side (AB), the side which is opposite to 90 °  is called hypotenuse side (AC) and remaining side is called adjacent side (BC).

Now, we need to find the distance between foot of the ladder and the wall. That is, we have to find the length of BC.

BC ≈  2(1.732)

BC  ≈ 3.464

So,  the distance between foot of the ladder and the wall is about 3.464 m.

Problem 3 :

A string of a kite is 100 meters long and it makes an angle of 60° with horizontal. Find the height of the kite, assuming that there is no slack in the string.

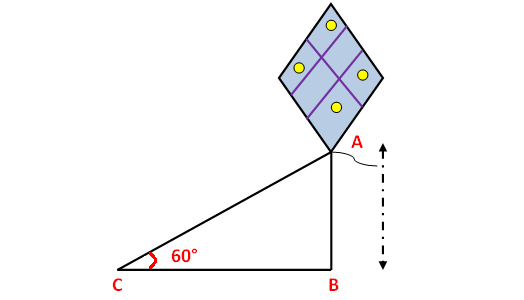
Here AB represents height of kite from the ground, BC represents the distance of kite from the point of observation.

In the right triangle ABC the side which is opposite to angle 60 °  is known as opposite side (AB), the side which is opposite to 90 °  is called hypotenuse side (AC) and remaining side is called adjacent side (BC).

Now we need to find the height of the side AB.

AB  ≈  50√3

AB  ≈  50(1.732)

AB  ≈ 86.6

So, the height of kite from the ground is about 86.6 m.

Problem 4 :

From the top of the tower 30 m height a man is observing the base of a tree at an angle of depression measuring 30 ° . Find the distance between the tree and the tower.

Draw a sketch. 

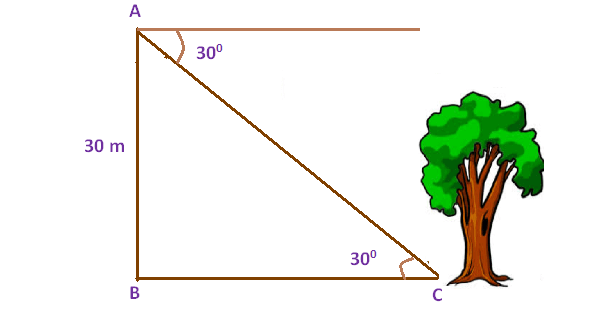
Here AB represents height of the tower, BC represents the distance between foot of the tower and the foot of the tree. 

Now we need to find the distance between foot of the tower and the foot of the tree (BC).

BC = 30(1.732)

 BC = 51.96

So, the distance between the tree and the tower is about 51.96 m.

Problem 5 :

A man wants to determine the height of a light house. He measured the angle at A and found that tan A = 3/4. What is the height of the light house if A is 40 m from the base?

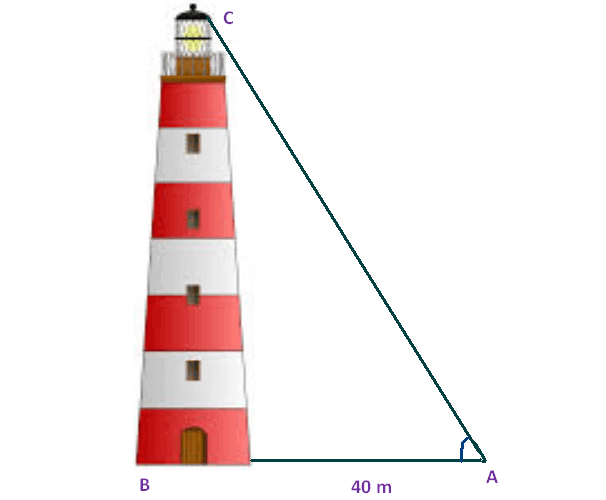
Here BC represents height of the light house, AB represents the distance between the light house from the point of observation. 

In the right triangle ABC the side which is opposite to the angle A is known as opposite side (BC), the side which is opposite to 90 °  is called hypotenuse side (AC) and remaining side is called adjacent side (AB).

Now we need to find the height of the light house (BC).

30 = BC 

So, the height of the light house is 30 m.

Problem 6 :

The length of a string between a kite and a point on the ground is 90 m. If the string is making an angle θ with the level ground  such that tan θ = 15/8, how high will the kite be ?

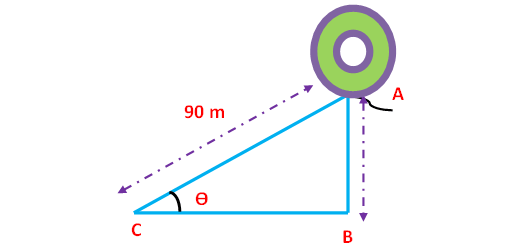
Here AB represents height of the balloon from the ground. In the right triangle ABC the side which is opposite to angle θ is known as opposite side (AB), the side which is opposite to 90 °  is called hypotenuse side (AC) and remaining side is called adjacent side (BC).

t anθ = ¹⁵⁄₈ -----> cotθ = ⁸⁄₁₅

Then, we have

AB  ≈  79.41

So, the height of the tower is about 79.41 m.

Problem 7 :

An aero plane is observed to be approaching the air point. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 50 ° . Find the height above the ground.

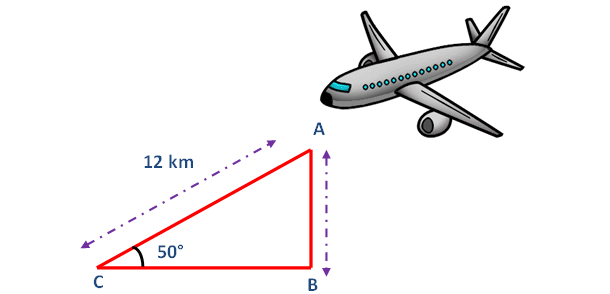
Here AB represents height of the airplane from the ground. In the right triangle ABC the side which is opposite to angle 50 °  is known as opposite side (AB), the side which is opposite to 90 °  is called hypotenuse side (AC) and remaining side is called adjacent side (BC).

From the figure given above, AB stands for the height of the aero plane above the ground. 

AB  ≈ 9.192 km

So, the height of the aero plane above the ground is about 9.192 km.

Problem 8 :

A balloon is connected to a meteorological station by a cable of length 200 m inclined at 60 °  angle . Find the  height of the balloon from the ground. (Imagine that there is no slack in the cable)

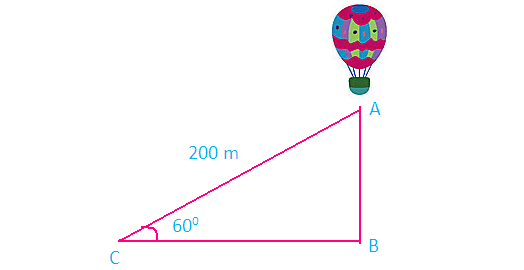
Here AB represents height of the balloon from the ground. In the right triangle ABC the side which is opposite to angle 60 °  is known as opposite side (AB), the side which is opposite to 90 °  is called hypotenuse (AC) and the remaining side is called as adjacent side (BC).

From the figure given above, AB stands for the height of the balloon above the ground. 

AB  ≈ 100(1.732)

AB ≈  173.2

So, the height of the balloon from the ground is about 173.2 m.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

The Mean Value Theorem Worksheet

May 14, 24 08:53 AM

Mean Value Theorem

May 14, 24 02:48 AM

How to Find the Vertex of a Parabola

May 12, 24 10:03 PM

• Heights and Distances

Trigonometry is the study of the relationship between the length of sides and angles of a triangle. A triangle is a closed shape consisting of three sides. The relation between the heights and distances of objects can be understood using trigonometry. We will learn about the same in this topic.

Suggested Videos

Trigonometry.

Trigonometry has found its importance in multiple fields. It has found its applications in the fields ranging from Engineering to Architecture to Astronomy as well. Trigonometry can be used in these fields by to measure distances and angles by assuming lines that connect the points.

You can download Some Applications of Trigonometry Cheat Sheet by clicking on the download button below

Height is the measurement of an object in the vertical direction and distance is the measurement of an object from a particular point in the horizontal direction. If we imagine a line connecting the point of observation to the topmost point of the object then the horizontal line, vertical line and the imaginary line will form a triangle.

Observe the figure. Consider the observer to be at point C. The height of the object is shown by line AB. The distance of the object from the observer is given by line BC. The object may or may not be perpendicular to the ground. Line AC represents the Line of Sight when the observer is observing the topmost point of the object. Angle α represents the angle of elevation and Angle β represents the angle of depression.

Using trigonometry, if we are provided with any of the two quantities that may be a side or an angle, we can calculate all the rest of the quantities. By the law of alternate angles, the angle of elevation and angle of depression are consequently equal in magnitude (α = β). Tan α is equal to the ratio of the height and distance.

You can be provided with any two of the following information:

• The distance of the object from the observer
• The height of the object
• Angle at which the observer views the topmost point of the object (angle of elevation)
• The angle at which the observer views the object when the observer is on top of a tower/building (angle of depression)

and you can calculate the rest. Here are some examples for you in the following section.

Solved Examples for You on Heights & Distances

Question 1: An observer 1.5 m tall is 28.5 m away from a tower. The angle of elevation of the top of the tower from his/her eyes has measure 45. What is the height of the tower?

We can form the above figure by given data, ⟹ B D = C E = 1.5

In Δ A B C , ∠ C B A = 90º ⟹ tan 45º = A B/ B C ⟹ 1 = A B/ 28.5 ⟹ A B = 28.5

Now, h = A B + B D = 28.5 + 1.5 = 30 Hence, the height of the tower is 30   m

Question 2: What does height mean?

Answer: Basically, height means altitude or elevation that refers to the distance above a level. Furthermore, height denotes extent upward (as from foot to head) as well as any measurable distance above a given level. For example, the height of a tree, human, mountain, tower, etc.

Question 3: What is the difference between height and hight?

Answer: The major difference between height and hight is that height refers to the distance between the highest and lowest end of an object. On the other hand, hight refers to a mountain located in the United States of America.

Question 4: How do you find the height of objects in math?

Answer: In mathematics, you can calculate the height of an object using the distance and angles. Here distance is the horizontal distance between the object and the angle is the angle above the horizontal of the top of the object, which gives the height of the object.

Question 5: What is the maximum height?

Answer: It refers to the highest vertical position along the path of its trajectory. Moreover, the maximum height of the projectile depends upon the velocity and angle of the launch of the object and the acceleration due to gravity.

Customize your course in 30 seconds

Which class are you in.

Some Applications of Trigonometry

One response to “heights and distances”.

Cant we calculate the distance by taking 90°

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

Heights and Distances: Trigonometry Applications, Examples, Formulas

Height and Distance : One of the main application of trigonometry is to find the distance between two or more than two places or to find the height of the object or the angle subtended by any object at a given point without actually measuring the distance or heights or angles. Trigonometry is useful to astronomers, navigators, architects and surveyors etc. in solving problems related to heights and distances.

Height and Distance

The directions of the objects can be described by measuring:

• Angle of elevation
• Angle of depression

Angles of elevation or angles of depression of the objects are measured by an instrument called Theodolite. Theodolite is based on the principles of trigonometry, which is used for measuring angles with a rotating telescope. In 1856, Sir George Everest first used the giant theodolite, which is now on display in the Museum of the survey of India in Dehradun

Angle of Elevation

Let P be the position of the object above the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of elevation . It is called the angle of elevation, because the observer has to elevate (raise) his line of sight from the horizontal OA to see the object P. [When the eye turns upwards above the horizontal line].

Line of sight : It is the line drawn from the eye of an observer to the object viewed.

Angle of Depression

Let P be the position of the object below the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of depression .

It is called the angle of depression because the observer has to depress (lower) his line of sight from the horizontal OA to see the object P.

[When the eye turns downwards below the horizontal line].

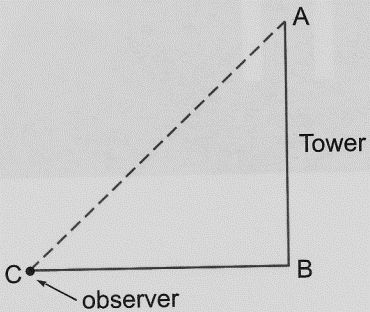
Below the eye level: If the object lies below the horizontal plane of our eyes, then we have to move our head downwards to view it. In doing so, our lines of sight moves downwards through an angle and the angle, which the line of sight now makes with the horizontal line, is called the angle of depression of the object from our eyes.

Example : Let OH be the horizontal line at the eye level. If a person at O looks at an object P lying below the eye level, then, ∠HOP is the angle of depression of P as seen from O.

Note : Angle of depression of P as seen from O = angle of elevation of O, as seen from P.

∴ ∠AOP = ∠OPH

Height and Distance Formulas

Trigonometry Ratios Table

Height and Distance Important Points

• In solving problems observer is represented by a point if his height is not given.

• A line drawn parallel to earth surface is called horizontal line.

• If the angle of elevation of sun decreases, then the length of shadow of an object increases and vice-versa.
• If in problems, the angle of elevation of an object is given, then we conclude that the object is at higher altitude than observer. The angle of depression implies that observer is at higher altitude than object.

Height and Distance Questions

1. If a pole 6 m high casts a shadow 2√3 m long on the ground, find the Sun’s elevation. [ NCERT Exemplar]

2. An observer 1.5 m tall is 20.5 m away from a tower 22 m high. Determine the angle of elevation of the top of the tower from the eye of the observer.

4. The ratio of the height of a tower and the length of its shadow on the ground is √3 : 1. What is the angle of elevation of the sun? [CBSE Delhi 2017]

5. If the angle of elevation of a tower from a distance of 100 m from its foot is 60°, then what will be the height of the tower? [NCERT Exemplar]

6. In Fig. 11.10, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder, (use √3 =1.73) [CBSE Delhi 2016]

7. An observer, 1.7 m tall, is 20 √3 m away from a tower. The angle of elevation from the eye of observer to the top of tower is 30°. Find the height of tower. [CBSE (F) 2016]

8. If a tower 30 m high, casts a shadow 10 √3 m long on the ground, then what is the angle of elevation of the sun ? [CBSE (AI) 2017]

Trigonometry Formulas

• [email protected]
• CA Mock Drill TM
• Test Series
• English Lang

Current Affairs Mock Drill 2024

Current affairs mock drill 2023, current affairs mock drill 2022, current affairs mock drill 2021.

Height and Distance Questions with Answers

Height and dist quiz 4, height and dist quiz 3, height and dist quiz 2, height and dist quiz 1.

Height and Distance topic is a fundamental part of trigonometry and is used in real-life applications to determine the distance between two or more than two places or to find the height of the object or the angle subtended by any object at a given point without actually measuring the distance or heights or angles. Height and distance questions are commonly asked in major competitive exams such as IBPS, RRB, CDS, SSC CHSL, SSC CGL, Railway, insurance, etc and you can find 2-3 questions from this topic in every exam. Smartkeeda offers a comprehensive collection of height and distance questions with answers, allowing you to practice and become acquainted with the question types commonly presented in this topic.

Height and distance topic generally deals with the measurement and calculation of vertical heights and horizontal distances between objects or points. A good knowledge of trigonometric ratios , including sine, cosine, and tangent, is essential for effectively solving height and distance questions. At Smartkeeda, you can practice height and distance questions with answers available on the website. Additionally, you download Height and Distance Questions PDFs, which serve as valuable resource for in-depth practice and proficiently handle a wide array of questions in your upcoming exams. ​​​​​​​

Frequently Asked Questions

• Toggle navigation

• CREST Mathematics Olympiad (CMO)
• CREST Science Olympiad (CSO)
• CREST English Olympiad (CEO)
• CREST Reasoning Olympiad (CRO)
• CREST Cyber Olympiad (CCO)
• CREST Mental Maths Olympiad (CMMO)
• International Green Warrior Olympiad (IGWO)
• CREST International Drawing Olympiad (CIDO)
• CREST International Spell Bee Summer (CSB)
• CREST International Spell Bee Winter (CSBW)
• International Teacher Olympiads
• Teacher Mathematics Olympiad
• Teacher Science Olympiad
• Teacher English Olympiad
• Exam Syllabus
• Sample Papers
• Previous Year Papers
• Marking Scheme
• Cut-Offs & Ranking Criteria
• Awards & Recognition
• Subject Rankers
• Subject Cut-Off
• Zone Definition
• Green Warrior Initiatives
• Rankholder's Gallery
• Testimonials
• Olympiad Exam Blog
• WhatsApp Channel
• Olympiad Books
• Live Classes
• CREST Fundamentals
• Mental Mathematics Olympiad (CMMO)
• Green Warrior Olympiad (IGWO)
• Country Wise Olympiads
• Student Registration
• Teacher Registration
• School Registration
• Become a Coordinator
• Special Needs Kids
• CMO arrow_drop_down
• CSO arrow_drop_down
• CEO arrow_drop_down
• CRO arrow_drop_down
• CCO arrow_drop_down
• CMMO arrow_drop_down
• IGWO arrow_drop_down
• CIDO arrow_drop_down
• CSB arrow_drop_down
• CSBW arrow_drop_down
• Individual Registration
• Register Your School
• Exam Schedule
• Ranking Criteria
• Become a Co-ordinator
• assignment_ind
• account_balance

Questions on Trigonometry: Height and Distance

• About Topic
• Practice Questions
• More Topics
• Register for CREST Olympiads
• Online Classes

Questions on Trigonometry: Height and Distance - Sub Topics

• Finding Height and Distance
• Line of Sight
• Angle of Elevation
• Angle of Depression
• Measure Angle with Clinometer
• Trigonometric Ratios

The reading material provided on this page for Finding Height and Distance using Trignometry is specifically designed for students in grades 9 and 10. So, let's begin!

How to Find Height and Distance using Trignometry?

Trigonometry has a wide range of practical applications, including the measurement of heights and distances between objects. One of the most common applications of trigonometry is to determine the distance between two or more points or to find the height of an object or the angle it subtends from a given point.

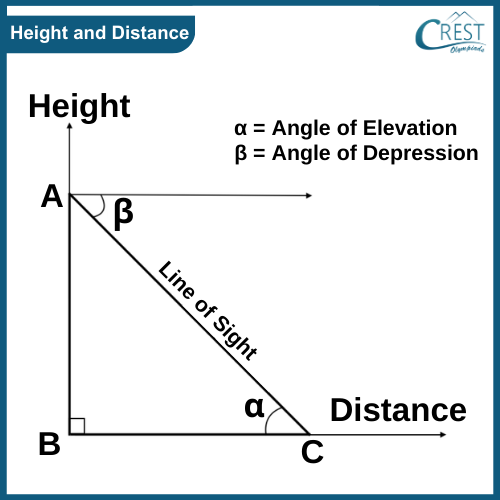
The following are the main definitions that are used when finding heights and distances:

1. Line of Sight 2. Angle of Elevation 3. Angle of Depression

What is Line of Sight?

The line of sight is the line that is drawn from the observer's eyes to the point being viewed on the object. It represents the direct path that light takes from the object to the observer's eye and is used to determine visibility and perspective in visual perception.

What is Angle of Elevation?

The angle of elevation is the angle between a horizontal line and a line of sight to an object above the horizontal. It is used to determine the height or distance of an object and is measured in degrees.

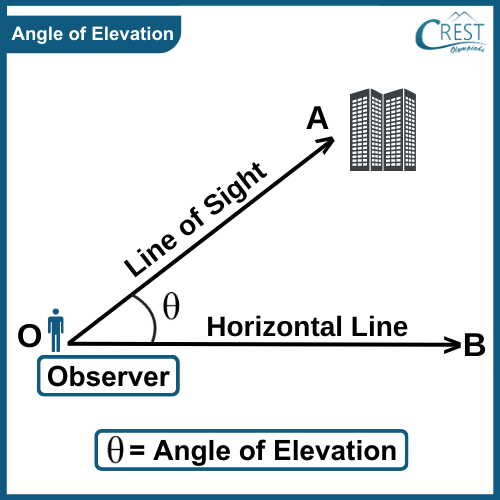
For example , when you look up at a tall building from a distance. The angle between the ground and your line of sight to the top of the building is the angle of elevation.

What is Angle of Depression?

The angle of depression is the angle between a horizontal line and a line of sight to an object below the horizontal. It is used to determine the depth or distance of an object and is measured in degrees.

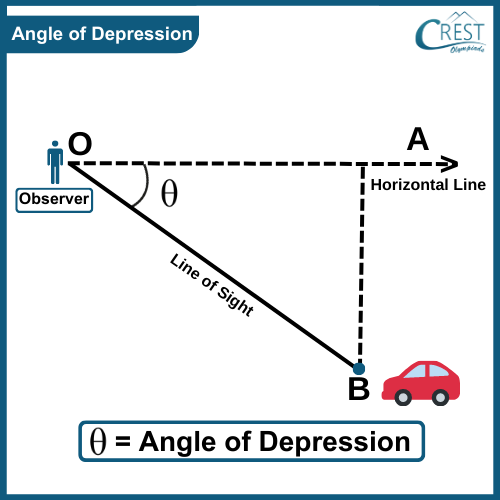
For example , if someone is standing on top of a hill and looking down at a car parked at the bottom of the hill, the angle of depression would be the angle formed between the horizon and the line of sight to the car.

How to Measure Angle with a Clinometer?

A clinometer is an instrument that is used to measure the angle of slope, inclination or elevation of an object.

What are Trigonometric Ratios?

Trigonometric ratios are mathematical expressions that relate the sides of a right triangle to its angles.

What are the 6 trigonometric ratios?

Trigonometric ratios are mathematical relationships that describe the ratios of the lengths of sides in a triangle. These ratios are specifically applicable to right triangles, where one angle measures 90 o . There are 3 primary trignometric ratios namely sine, cosine, and tangent whereas it also encompasses three other ratios such as secant, cosecant and cotangent. These ratios, commonly abbreviated as sin, cos, tan, sec, cosec and cot, respectively, represent the relationships between the sides of a right triangle and the angles within it. By knowing the measure of an acute angle, denoted as θ, one can calculate the values of these trigonometric ratios for the given triangle.

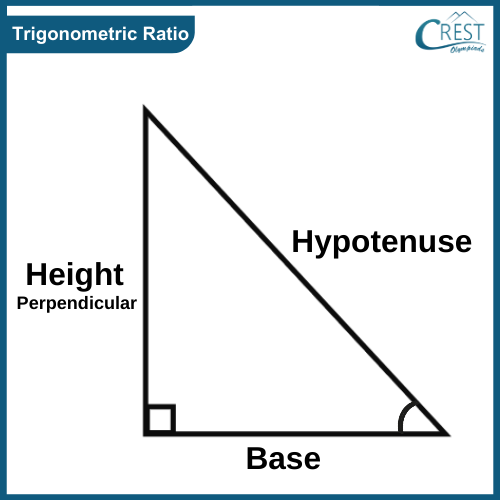
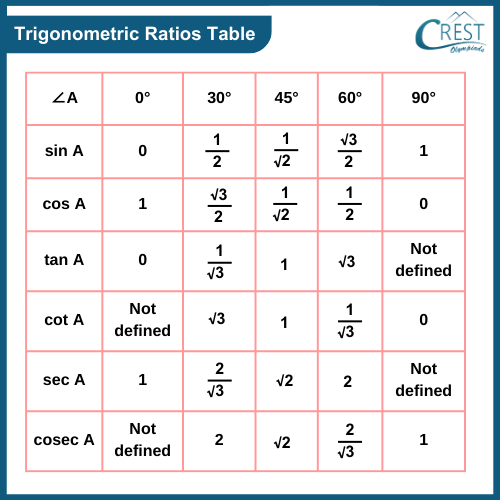
Trignometric Ratios Table

The table provided can assist in solving height and distance problems by utilizing trigonometric ratios.

Share Your Feedback

CREST Olympiads has launched this initiative to provide free reading and practice material. In order to make this content more useful, we solicit your feedback.

Do share improvements at [email protected]. Please mention the URL of the page and topic name with improvements needed. You may include screenshots, URLs of other sites, etc. which can help our Subject Experts to understand your suggestions easily.

Mental Maths Related Topics

• Solved Questions of Probability
• Types of Decimal Expansion
• Rules and Tricks on Simplification
• Polynomials and its Types
• Circle - Definition, Parts, Formula
• Questions on Boats and Streams
• Quadratic Equations - Sub Topics
• Worksheet of Alphanumeric Series
• Data Interpretation - Types of Graphs, Solved Questions
• What is Statistics?
• Solved Questions on Area of Triangle

Talk to our experts

1800-120-456-456

Height and Distance

• Height And Distance

Height and Distance is a part of trigonometry which is studied by scholars from all over the world. It is used to calculate distances from the Earth to the planets and stars since years. One of the best uses of height and distance was in finding the height of the highest mountain in the world that is Mount Everest named after Sir George Everest. It was the Great Trigonometric Survey conducted by British India in 1852 where the height of Mt. Everest was found out from a distance of 160 km by using the instrument the Giant Theodolites. In recent days, we use the concept of height and distance in the detection of crime, marine biology, navigation, military, calculus, astronomy, aviation, etc. It is also helpful to measure the height of the mountain, pillar, building, monument, etc.

Height and Distance Concept

Height and distance of anything can be found by using Trigonometric formulas. You can find the height of Qutub Minar if you know the distance of your position from Qutub Minar and the angle at which you are able to see the top of the Minar. To find the height we use trigonometry because the surface of the ground, the height of Minar and the line of elevation all together form a right angle triangle with 90 degrees between the Minar and the ground. 

Distance is usually the ‘base’ of the right-angled triangle formed by the height of Minar and line of sight. The length of the horizontal level also tells us the distance, as it also forms the base of the triangle which is at a certain height but parallel to the ground. Line of sight forms the ‘hypotenuse’ of the right-angled triangle. The line perpendicular to the ground forms the ‘height’ of the triangle.

To calculate the angle of elevation or depression we can use the following formula: 

\[\sin \theta  = \frac{{Height}}{{Hypotenuse}}.\cos \theta  = \frac{{Base}}{{Hypotenuse}},\tan \theta = \frac{{Height}}{{Base}}\]

Here, θ is either the angle of elevation or depression.

Terms Related to Height and Distance

Line of Sight: It is the straight line that is drawn from the eye of an observer to the point of an object which is to be viewed.

Horizontal Level: It is the horizontal line drawn from the eye of the viewer.

The angle of elevation: It is the angle formed between the line of sight and horizontal level if the object is above the horizontal level.

The Angle of Depression: It is the angle formed between the line of sight and the horizontal level if the object is below the horizontal level.

Pythagorean Theorem 

Since height and distance involve a right-angled triangle so Pythagoras theorem can be used to find the length of the sides. Pythagoras theorem states that the square of the hypotenuse of a right-angled triangle is equal to the sum of the square of its base and height. 

\[{\left( {Hypotenuse} \right)^2} = {\left( {Base} \right)^2} + {\left( {Perpendicular} \right)^2}\]

If the length of the base, perpendicular and hypotenuse of a right-angle triangle is a, b and c respectively. 

Then,  a 2 + b 2 = c 2 .

Thus, if the length of any two sides is known then the length of the third side can be found by using the Pythagoras theorem which is also called the Pythagorean triple. 

Height and Distance Solved Examples:

An observer 1.5m tall is 28.5 m away from a chimney. The angle of elevation of the top of the chimney from her eyes is 45 degrees. What is the height of the chimney?

Here, AB is the chimney, CD the observer and angle ADE is the angle of elevation. In this case, ADE is a triangle, right-angled at E and we are required to find the height of the chimney.

AB = AE + BE = AE + 1.5

and DE = CB = 28.5m

To determine AE, we choose a trigonometry ratio, which involves both AE and DE. Let us choose the tangent of the angle of elevation.

Now,   tan 45 o = AE/DE

                    1 = AE/28.5

                   AE = 28.5 

So the height of the chimney (AB) = (28.5 + 1.5)m = 30m.

From a point P on the ground, the angle of elevation of the top of a 10m tall building is 30degree. A flag is hoisted at the top of the building and the angle of elevation of the top of flagstaff from P is 45 degrees. Find the length of the flagstaff and the distance of the building from point P.

AB denotes the height of the building. BD the flag and P the given point. Note that there are two right triangles PAB and PAD. We are required to find the length of the flagstaff, i.e., DB and the distance of the building from the point, i.e, PA.

Since we know the height of the building AB, we will first consider the right PAB.

We have tan30 o = \[\frac{AB}{AP}\]

i.e,         \[\frac{1}{\sqrt{3}}\] = \frac{10}{AP}\]

Therefore, AP = 10 \[\sqrt{3}\].

i.e, the distance of the building from P is 10 root 3 m = 17.32m.

Next, let us suppose DB = xm. Then AD = (10+x)m.

Now, in right triangle PAD, 

tan 45 degree = \[\frac{{AD}}{{AP}} = \frac{{\left( {10 + x} \right)}}{{\left( {10{\text{ }}root{\text{ }}3} \right)}}\]

Therefore, 1= \[\frac{(10+x)}{10\sqrt{3}}\]

i.e,  x= 10(\[\sqrt{3}\] - 1) = 7.32.

So, the length of the flagstaff is 7.32m.

Summary of the Types of Problems:

Practical application of height and distance:.

The concept of Height and Distance are used in various fields like:

To Find the Slope and Height During Construction:

We can find the height of a building or monument if the angle of elevation and the distance of the building is given. Similarly, the determination of angle of elevation, angle of depression and distance of the object can be found out if the other pieces of information are given.

The Use of Trigonometry to Measure the Height of a Mountain or a Building:

Basically, the height of the mountain or building can be easily measured using the trigonometric ratios. Consider the base of the mountain or building as adjacent and the height as opposite, then the third-longest part of the triangle will be hypotenuse as shown above in the figure. Triangle should be a right-angled triangle. Hence, this is the real-life application of trigonometry.                                        

To Calculate the Angle of Elevation or Depression Required to Reach the Target:

Incase of aviation, wind plays a most important role. In aviation, the angle of depression and the angle of elevation is used depending on the case. The angle of depression is when the line of sight to the object is below the horizontal line and the angle of elevation is when the line of sight to the object is above the horizontal line.

The wind of flight direction is considered as the two perpendicular sides of a right-angled triangle in which the speed of the flight and the speed of wind are measured in their direction. 

Explanation: From the above figure, the distance between the plane and the final point is one of the perpendicular distances. The distance of the plane from the ground is another perpendicular distance. Slant distance is the hypotenuse.

For this, trigonometric ratios are used for finding the distance or angle of aviation.

To Calculate the Height of the Criminal or Angle of the Gun:

In criminology, trigonometry can be used to find the shots of bullet or how tall the shooter was. This helps the police in the investigation. For this also trigonometric ratios are used i.e., sine, cosine, tangent. This is also the real-life application of trigonometry.

From the figure, it can be clearly seen that the triangulation is done through which the distance and angle can be found.

To Find the Distance or the Angle of Movement of Marine Organisms:

Marine Biology is the study of marine life. In marine biology, the biologists study marine life like plants, animals and other organisms that live there.

In marine biology, for predicting how far and at what angle the organism or plant is from the observer, trigonometry concepts are used.

Here, the water level is the base of the right-angled triangle and 

the depth of the object is the height 

slant distance is the line of sight 

Angle could be an angle of depression or angle of elevation, it depends on the observer who is observing.                  

Hence, trigonometry ratio and formula are used for finding the distance, angle.

Hence the exact location of the underwater living or non- living things can be measured easily with the help of trigonometry ratios sine, cosine and tangent. Hence, this is again a real life application of trigonometry.

To Control the Movement of Vehicles:

In navigation, controlling and monitoring of moving vehicles are studied. In this, the movement of the plane, ships, submarines, etc is studied. Navigation is of many types- marine navigation, aeronautical navigation, space navigation, and land navigation. Navigation is the study of moving objects and the angle or distance is measured using the concept of trigonometry at that point where we have to measure.

To measure the exact location of the moving body, compass, pinpoint poles, trigonometric ratios and formula are used.

To Find the Position and Angle of Satellite:

In satellite, trigonometry is used. Where the satellite is and at what angle this all can be easily measured using the trigonometry. Exact location or position of the satellite can be easily measured using the trigonometric ratios.

NCERT Study Material

• Trending Now
• Foundational Courses
• Data Science
• Practice Problem
• Machine Learning
• System Design
• DevOps Tutorial
• Pipes and Cistern - Aptitude Questions and Answers
• Speed, Time and Distance – Formulas & Aptitude Questions
• Boats and Streams - Aptitude Questions and Answers
• Percentages - Aptitude Questions and Answers
• Ratio and Proportion - Aptitude Questions and Answers
• Alligation or Mixture - Aptitude Questions and Answers
• Algebra From Basics to Advanced : Definition, Branches, Examples
• Problems on Ages - Aptitude Questions and Answers
• Profit and Loss - Aptitude Questions and Answers
• Simple Interest
• Compound Interest - Aptitude Questions and Answers
• Mensuration 2D Formula & Aptitude Questions
• Mensuration 3D Formulas and Aptitude Questions
• Height and Distances - Aptitude Questions and Answers
• Progression - Aptitude Questions and Answers
• Permutation and Combination - Aptitude Questions and Answers
• Probability - Aptitude Questions and Answers
• Clock - Aptitude Questions and Answers
• Calendar - Aptitude Questions and Answers
• Races and Games - Aptitude Questions and Answers
• Data Interpretation - Aptitude Question and Answers
• Data Sufficiency in Logical Reasoning
• Course of Action: Logical Reasoning Questions

Height and Distances – Aptitude Questions and Answers

Solving height and distance questions requires a strong knowledge of trigonometric principles. These types of problems come up frequently on various competitive examinations, like the SSC, Bank PO, and other government job exams, and are an integral part of Quantitative Aptitude . To make sure you do well on these tests, it’s important to learn how to calculate heights, distances, and angles between two or more objects. With practice and by studying the answers to some sample questions, you’ll be able to ace height and distance questions on your next competitive examination!

Practice Quiz :

Practice Height and Distances Aptitude Quiz Question

Height and Distance – Formulas

Sure, here’s a table containing important formulas related to height and distance:

sin θ = Perpendicular / Hypotenuse cos θ = Base / Hypotenuse tan θ = Perpendicular / Base cosec θ = Hypotenuse / Perpendicular sec θ = Hypotenuse / Base cot θ = Base / Perpendicular sin^2 θ + cos^2 θ = 1 1 + tan^2 θ = sec^2 θ 1 + cot^2 θ = cosec^2 θ

Sample Questions on Height and Distances

Q1: from the top of a lighthouse, the angles of depression of two ships are 30 and 45 degrees. the two ships, as it was observed from the top of the lighthouse, were 100 m apart. find the height of the lighthouse..

Solution : 

Here, we can apply the formula Height = Distance / [cot(original angle) – cot(final angle)] => Height of the lighthouse = 100 / (cot 30 – cot 45) = 100 / (√3 – 1) = 50 √3 + 50 m

Q2: A 80 m long ladder is leaning on a wall. If the ladder makes an angle of 45 degrees with the ground, find the distance of the ladder from the wall.

  Here, cos θ = Base / Hypotenuse => cos 45 = Base / 80 => Base = 80 cos 45 = 80 / √2= 40 √2 => Distance of the ladder from the wall = 40 √2 m

Q3: There are two poles, one on each side of the road. The higher pole is 54 m high. From the top of this pole, the angle of depression of the top and bottom of the shorter pole is 30 and 60 degrees respectively. Find the height of the shorter pole.

Let AB and CD be the two poles. Let AC = x m and CD = h m Now, in triangle ABC, tan 60 = AB / AC => √3 = 54 / AC => AC = 18 √3 m Clearly, AC = DE = 18 √3 m In triangle BED, tan 30 = BE / DE => BE = DE tan 30 => BE = 18 √3 / √3 m => BE = 18 m => CD = AE = AB – BE => CD = 54 – 18 = 36 m Therefore, the height of the shorter pole = 36 m

Q4: From the top of a tower 100m high, a person observes that the angle of elevation of the top of another tower is 60° and the angle of depression of the bottom of the tower is 30°. Then the height (in meters) of the second tower is.

Let AB be the first tower and CD be the second tower. From figure, Tan(30)= BC/AB => AB=BC/√3 Tan(60)=CD/AB => CD=AB√3 = BC/√3 * √3 = BC Total height of the second tower = CD + BD BD = AB – AD => BD= BC/√3 – 100 => Height of second tower = BC + BC/√3 – 100 = BC ( 1+ 1/√3) – 100 = BC (1+ √3/3) – 100 From the right-angled triangle, BC = AB cot 30 = AB/√3 = BC/3 Hence, Height of second tower = BC (1+ √3/3) – 100 = BC (4+ √3)/3 – 100 = BC (4+ √3)/3 – 300/3 = BC (4+√3)/3 – 100 = BC (4+ √3)/3 – 100 = 75 m (approx)

Q5: The angle of elevation of the top of a tower from point A on the ground is 45°. On moving 20 meters toward the tower, the angle of elevation of the top of the tower becomes 60°. Find the height of the tower (in meters).

Let h be the height of the tower and x be the distance between the initial position and the foot of the tower. From the right-angled triangle AOB, where O is the foot of the tower, we have: tan(45°) = h / x => h = x From the right-angled triangle COB, where C is the new position of the observer, we have: tan(60°) = h / (x – 20) => h = (x – 20) × √3 Equating both expressions for h, we get: x = (x – 20) × √3 Simplifying, we get: x = 20 × (√3 + 1) Therefore, the height of the tower is: h = x = 20 × (√3 + 1) meters, which is approximately 45.72 meters (rounded to two decimal places).

Related Resources: 

Problems on Height and Distances | Set-2

Test your knowledge of Height and Distance in Quantitative Aptitude with the quiz linked below, containing numerous practice questions to help you master the topic:-

<< Practice Height and Distance Aptitude Questions >>

Also Practice:

Mensuration 2D Aptitude Questions Mensuration 3D Aptitude Questions Permutation and Combination Aptitude Questions

Please Login to comment...

Similar reads.

• QA - Placements

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Math Article

Trigonometry

Trigonometry is one of the important branches in the history of mathematics  that deals with the study of the relationship between the sides and angles of a   right-angled triangle. This concept is given by the Greek mathematician Hipparchus. In this article, we are going to learn the basics of trigonometry such as trigonometry functions, ratios, trigonometry table, formulas and many solved examples.

What is Trigonometry?

Trigonometry is one of the most important branches in mathematics that finds huge application in diverse fields. The branch called “Trigonometry” basically deals with the study of the relationship between the sides and angles of the right-angle triangle.  Hence, it helps to find the missing or unknown angles or sides of a right triangle using the trigonometric formulas, functions or trigonometric identities. In trigonometry, the angles can be either measured in degrees or radians. Some of the most commonly used trigonometric angles for calculations are 0°, 30°, 45°, 60° and 90°. 

Trigonometry is further classified into two sub-branches. The two different types of trigonometry are:

• Plane Trigonometry
• Spherical Trigonometry

In this article, let us discuss the six important trigonometric functions, ratios, trigonometry table, formulas and identities which helps to find the missing angles or sides of a right triangle.

Trigonometry Ratios-Sine, Cosine, Tangent

The trigonometric ratios of a triangle are also called the trigonometric functions. Sine, cosine, and tangent are 3 important trigonometric functions and are abbreviated as sin, cos and tan. Let us see how are these ratios or functions, evaluated in case of a right-angled triangle.

Consider a right-angled triangle, where the longest side is called the hypotenuse, and the sides opposite to the hypotenuse are referred to as the adjacent and opposite sides.

Six Important Trigonometric Functions

The six important trigonometric functions (trigonometric ratios) are calculated using the below formulas and considering the above figure. It is necessary to get knowledge about the sides of the right triangle because it defines the set of important trigonometric functions.

Even and Odd Trigonometric Functions

The trigonometric function can be described as being even or odd.

Odd trigonometric functions: A trigonometric function is said to be an odd function if f(-x) = -f(x) and symmetric with respect to the origin.

Even trigonometric functions: A trigonometric function is said to be an even function, if f(-x) = f(x) and symmetric to the y-axis.

We know that

• Sin (-x) = – Sin x
• Cos (-x) = Cos x
• Tan (-x) = -Tan x
• Csc (-x) = – Csc x
• Sec (-x) = Sec x
• Cot (-x) = -Cot x

Therefore, cosine and secant are the even trigonometric functions, whereas sine, tangent, cosecant and cotangent are the odd trigonometric functions. If we know the even and odd trigonometric functions, it helps us to simplify the trigonometric expression when the variable inside the trigonometric function is negative.

Trigonometry Angles

The trigonometry angles which are commonly used in trigonometry problems are  0 ° , 30 ° , 45 ° , 60 ° and 90 °. The trigonometric ratios such as sine, cosine and tangent of these angles are easy to memorize. We will also show the table where all the ratios and their respective angle’s values are mentioned. To find these angles we have to draw a right-angled triangle, in which one of the acute angles will be the corresponding trigonometry angle. These angles will be defined with respect to the ratio associated with it.

For example, in a right-angled triangle,

Sin θ = Perpendicular/Hypotenuse

or θ = sin -1  (P/H)

θ = cos -1  (Base/Hypotenuse)

θ = tan -1  (Perpendicular/Base)

Trigonometry Table

Check the table for common angles which are used to solve many trigonometric problems involving trigonometric ratios.

In the same way, we can find the trigonometric ratio values for angles beyond 90 degrees, such as 180°, 270° and 360°.

Unit Circle

The concept of unit circle helps us to measure the angles of cos, sin and tan directly since the centre of the circle is located at the origin and radius is 1. Consider theta be an angle then,

Suppose the length of the perpendicular is y and of base is x. The length of the hypotenuse is equal to the radius of the unit circle, which is 1. Therefore, we can write the trigonometry ratios as;

List of Trigonometry Formulas

The Trigonometric formulas or Identities are the equations which are true in the case of Right-Angled Triangles. Some of the special trigonometric identities are given below –

• Pythagorean Identities
• sin²θ + cos²θ = 1
• tan 2 θ + 1 = sec 2 θ
• cot 2 θ + 1 = cosec 2 θ
• sin 2θ = 2 sin θ cos θ
• cos 2θ = cos²θ – sin²θ
• tan 2θ = 2 tan θ / (1 – tan²θ)
• cot 2θ = (cot²θ – 1) / 2 cot θ
• Sum and Difference identities-

For angles u and v, we have the following relationships:

• sin(u + v) = sin(u)cos(v) + cos(u)sin(v)
• cos(u + v) = cos(u)cos(v) – sin(u)sin(v)
• \(\begin{array}{l}tan(u+v) = \frac{tan(u)\ +\ tan(v)}{1-tan(u)\ tan(v)}\end{array} \)
• sin(u – v) = sin(u)cos(v) – cos(u)sin(v)
• cos(u – v) = cos(u)cos(v) + sin(u)sin(v)
• \(\begin{array}{l}tan(u-v) = \frac{tan(u)\ -\ tan(v)}{1+tan(u)\ tan(v)}\end{array} \)
• If A, B and C are angles and a, b and c are the sides of a triangle, then,
• a/sinA = b/sinB = c/sinC

Cosine Laws

• c 2  = a 2  + b 2  – 2ab cos C
• a 2  = b 2  + c 2  – 2bc cos A
• b 2  = a 2  + c 2  – 2ac cos B

Trigonometry Identities

The three important trigonometric identities are:

• tan² θ + 1 = sec² θ
• cot ² θ + 1 = cosec² θ

Euler’s Formula for trigonometry

As per the euler’s formula, 

e ix = cos x + i sin x

Where x is the angle and i is the imaginary number. 

\(\begin{array}{l}\sin x=\frac{e^{i x}-e^{-i x}}{2 i}\\ \cos x=\frac{e^{i x}+e^{-i x}}{2}\\  \tan x=\frac{\left(e^{i x}-e^{-i x}\right)}{i\left(e^{i x}+e^{-i x}\right)}\end{array} \)

Trigonometry Basics

The three basic functions in trigonometry are sine, cosine and tangent. Based on these three functions the other three functions that are cotangent, secant and cosecant are derived. 

All the trigonometrical concepts are based on these functions. Hence, to understand trigonometry further we need to learn these functions and their respective formulas at first.

If θ is the angle in a right-angled triangle, then 

Cos θ = Base/Hypotenuse

Tan θ = Perpendicular/Base

Perpendicular is the side opposite to the angle θ.

The base is the adjacent side to the angle θ.

The hypotenuse is the side opposite to the right angle

The other three functions i.e. cot, sec and cosec depend on tan, cos and sin respectively, such as:

Cot θ = 1/tan θ

Sec θ = 1/cos θ

Cosec θ = 1/sin θ

Cot θ = Base/Perpendicular

Sec θ = Hypotenuse/Base

Cosec θ = Hypotenuse/Perpendicular

Trigonometry Examples

There are many real-life examples where trigonometry is used broadly.

If we have been given with height of the building and the angle formed when an object is seen from the top of the building, then the distance between object and bottom of the building can be determined by using the tangent function, such as tan of angle is equal to the ratio of the height of the building and the distance. Let us say the angle is ∝, then

Tan ∝ = Height/Distance between object & building

Distance = Height/Tan ∝

Let us assume that height is 20m and the angle formed is 45 degrees, then 

Distance = 20/Tan 45°

Since, tan 45° = 1

So, Distance = 20 m

Applications of Trigonometry

• Its applications are in various fields like oceanography, seismology, meteorology, physical sciences, astronomy, acoustics, navigation, electronics, etc.
• It is also helpful to measure the height of the mountain, find the distance of long rivers, etc.

Video Lesson on Applications of Trigonometry

Trigonometry Problems and Solutions

Example 1 : Two friends, Rakesh and Vishal started climbing a pyramid-shaped hill. Rakesh climbs 315 m and finds that the angle of depression is 72.3 degrees from his starting point. How high is he from the ground?

Solution : Let m is the height above the ground.

To find: Value of m

To solve m, use the sine ratio.

Sin 72.3° = m/315

0.953 = m/315

m= 315 x 0.953

m=300.195 mtr

The man is 300.195 mtr above the ground.

Example 2: A man is observing a pole of height 55 foot. According to his measurement, pole cast a 23 feet long shadow. Can you help him to know the angle of elevation of the sun from the tip of shadow?

Let x be the angle of elevation of the sun, then

tan x = 55/23 = 2.391

x = tan -1 (2.391)

or x = 67.30 degrees

Trigonometry Questions

Practise these questions given here to get a deep knowledge of Trigonometry. Use the formulas and table given in this article wherever necessary.

Q.1: In △ABC, right-angled at B, AB=22 cm and BC=17 cm. Find:

(a) sin A Cos B

(b) tan A tan B

Q.2: If 12cot θ= 15, then find sec θ.

Q.3: In Δ PQR, right-angled at Q, PR + QR = 30 cm and PQ = 10 cm. Determine the values of sin  P,  cos  P  and tan  P.

Frequently Asked Questions on Trigonometry

What do you mean by trigonometry.

Trigonometry is one of the branches of mathematics which deals with the relationship between the sides of a triangle (right triangle) with its angles. There are 6 trigonometric functions for which the relation between sides and angles are defined. Learn more about trigonometry now by visiting BYJU’S.

What are the six basic Trigonometric Functions?

There are 6 trigonometric functions which are:

• Sine function
• Cosine function
• Tan function
• Sec function
• Cot function
• Cosec function

What is the formula for six trigonometry functions?

What is the primary function of trigonometry, who is the founder of trigonometry, what are the applications of trigonometry in real life.

One of the most important real-life applications of trigonometry is in the calculation of height and distance. Some of the sectors where the concepts of trigonometry are extensively used are aviation department, navigation, criminology, marine biology, etc. Learn more about the applications of trigonometry here.

Learn about Trigonometry in a simple manner with detailed information, along with step by step solutions to all questions, only at BYJU’S. Download the app to get personalised videos.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

It’s a detailed explanation. Helps for my kid exam preparation

Gives a very good explanation. Best for the beginner’s as well as professional

That is my very nice topic in mathematics. Am very happy to this topic tank to all mathemateciat

it’s very nice topic in mathematics.

I very happy with this topic is a very nice topic in mathematics

Very nice explain 😃

So brilliant, well explained.

Best way of teaching Keep it up

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.