The Number e, Natural Logarithm and Common Logarithm
Related Topics: More Lessons for High School Regents Exam Math Worksheets
High School Math based on the topics required for the Regents Exam conducted by NYSED: The Number e and the Natural Logarithm, Common Logarithms and Natural Logarithms, Evaluating Common Logs and Natural Logs Using a Calculator.
Evaluating Common Logs and Natural Logs Using a Calculator

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 2 > Unit 8
- Solving exponential equations using logarithms: base-10
Solving exponential equations using logarithms
- Solve exponential equations using logarithms: base-10 and base-e
- Solving exponential equations using logarithms: base-2
- Solve exponential equations using logarithms: base-2 and other bases
Solving exponential equations of the form a ⋅ b x = d
Check your understanding.
- (Choice A) x = log 2 ( 39.3 ) A x = log 2 ( 39.3 )
- (Choice B) x = log 6 ( 118 ) B x = log 6 ( 118 )
- (Choice C) x = log 12 ( 236 ) C x = log 12 ( 236 )
- (Choice D) x = log 118 ( 6 ) D x = log 118 ( 6 )
- Your answer should be
- an integer, like 6
- a simplified proper fraction, like 3 / 5
- a simplified improper fraction, like 7 / 4
- a mixed number, like 1 3 / 4
- an exact decimal, like 0.75
- a multiple of pi, like 12 pi or 2 / 3 pi
Solving exponential equations of the form a ⋅ b c x = d
- (Choice A) t = log ( 43.5 ) A t = log ( 43.5 )
- (Choice B) t = log 30 ( 130.5 ) B t = log 30 ( 130.5 )
- (Choice C) t = log ( 174 ) 4 C t = log ( 174 ) 4
- (Choice D) t = log 30 ( 522 ) 4 D t = log 30 ( 522 ) 4
Challenge problem
- (Choice A) 2 A 2
- (Choice B) 3 B 3
- (Choice C) 4 C 4
- (Choice D) log 2 ( 3 ) D log 2 ( 3 )
- (Choice E) log 3 ( 2 ) E log 3 ( 2 )
- (Choice F) log ( 3 ) F log ( 3 )
Want to join the conversation?
- Upvote Button navigates to signup page
- Downvote Button navigates to signup page
- Flag Button navigates to signup page

Want Better Math Grades?
✅ Unlimited Solutions
✅ Step-by-Step Answers
✅ Available 24/7
➕ Free Bonuses ($1085 value!)
On this page
- Exponential & Logarithmic Functions
- 1. Definitions: Exponential and Logarithmic Functions
- 2. Graphs of Exponential and Logarithmic Equations
- 3. Logarithm Laws
- 4. Logarithms to Base 10
- 5. Natural Logarithms (base e)
- Dow Jones Industrial Average
- Calculating the value of e
- 6. Exponential and Logarithmic Equations
- World Population Live
- 7. Graphs on Logarithmic and Semilogarithmic Axes
- Interactive Log Table
Related Sections
Math Tutoring
Need help? Chat with a tutor anytime, 24/7.
Online Math Solver
Solve your math problem step by step!
IntMath Forum
Get help with your math queries:
5. Natural Logarithms (to the base e)
by M. Bourne
Later On this Page
Change of base
The number e frequently occurs in mathematics (especially calculus) and is an irrational constant (like π ). Its value is e = 2.718 281 828 ...
Apart from logarithms to base 10 which we saw in the last section, we can also have logarithms to base e . These are called natural logarithms .
We usually write natural logarithms using `ln`, as follows:
`ln x` to mean `log_e x` (that is, "`log x` to the base `e`")
Natural logarithms are commonly used throughout science and engineering. (For example, see Applications of Derivatives of Logarithms .)
Where does this value " e " come from? Go to Calculating the Value of e to find out.

NOTE: Please don't write natural log as
" In " (as in "She lives IN Singapore.")
Make sure it is
" " (as in L for logarithm and N for natural).
I know it looks like " In " on your calculator because of the font they use, but you only confuse yourself if you don't write it properly.
Actually, the `ln` notation confuses a lot of students and it would be better if we (and calculators) wrote it our in full. That is `log_e`.
Find the natural logarithm of `9.178`.
This means "Find `log_e 9.178`", which we can also write as "Find `ln 9.178`".
Using our calculator, we get
ln 9.178 = 2.2168
Check: Using the definition of a logarithm, we check as follows: `2.718\ 281\ 828 ^2.2168 = 9.1781`.
It checks OK.
Change of Base
At times we need to change from one base to another. The change of base formula (to change from base a to base b ) is as follows:
`log_b x=(log_a x)/(log_a b)`
Find the value of `log_3 8.7`.
[This problem is the same as answering: `3^?= 8.7`].
We cannot find `log_3 8.7` on a calculator. We need to use the change of base formula.
In this case, `b = 3` and `x = 8.7`.
`log_3 8.7=(log_10 8.7)/(log_10 3)` `=0.9395192/0.4771212` `=1.9691414`
CHECK: By calculator, `3^1.9691414 = 8.6999989`.
[We could have used natural logs as well, `log_3 8.7=(ln 8.7)/(ln 3)` which will give us the same answer.]
1. Use logarithms to base `10` to find `log_2 86`.
We estimate an answer in the range: `6` to `7`, because `2^6=64` and `2^7=128`, and `86` is between these 2 values.
`log_2 86 = (log 86)/(log 2)` `=1.934498451/0.301029995` `=6.426264755`
Our answer is between `6` and `7`, as expected.
2. Find the natural logarithm of `1.394`.
`ln 1.394 = 0.332177312`
Check: This means `e^0.332177312=1.394`
See also the Interactive Log Table where you can easily find log values to different bases.
Application of Exponential Functions
Here is an exponential graph which made lots of people very RICH (as long as they sold out at the peak).
Check out the Dow Jones Industrial Average graph .
Tips, tricks, lessons, and tutoring to help reduce test anxiety and move to the top of the class.
Email Address Sign Up

The Natural Base e
Popular tutorials in the natural base e.

How Do You Graph the Natural Base Exponential Function?
Want to graph a natural base exponential function? Make a table of points! Then plot the points, connect them, and you have your graph! Follow along with this tutorial to see the entire process step-by-step.

In math, 'e' isn't just a letter, it's an irrational number! This tutorial shows you how mathematicians use the letter 'e' to represent a specific value and how having a base of 'e' is called a natural base.

What is the Natural Base Exponential Function?
The natural base exponential function is actually a function that's shorter than its name! This tutorial introduces you to this special function and shows you what it looks like.
Related Topics
Other topics in natural base e and natural logarithms :.
- Natural Logarithms
- Terms of Use
6.6 Exponential and Logarithmic Equations
Learning objectives.
In this section, you will:
- Use like bases to solve exponential equations.
- Use logarithms to solve exponential equations.
- Use the definition of a logarithm to solve logarithmic equations.
- Use the one-to-one property of logarithms to solve logarithmic equations.
- Solve applied problems involving exponential and logarithmic equations.
In 1859, an Australian landowner named Thomas Austin released 24 rabbits into the wild for hunting. Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions.
Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions.
Using Like Bases to Solve Exponential Equations
The first technique involves two functions with like bases. Recall that the one-to-one property of exponential functions tells us that, for any real numbers b , b , S , S , and T , T , where b > 0 , b ≠ 1 , b > 0 , b ≠ 1 , b S = b T b S = b T if and only if S = T . S = T .
In other words, when an exponential equation has the same base on each side, the exponents must be equal. This also applies when the exponents are algebraic expressions. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. Then, we use the fact that exponential functions are one-to-one to set the exponents equal to one another, and solve for the unknown.
For example, consider the equation 3 4 x − 7 = 3 2 x 3 . 3 4 x − 7 = 3 2 x 3 . To solve for x , x , we use the division property of exponents to rewrite the right side so that both sides have the common base, 3. 3. Then we apply the one-to-one property of exponents by setting the exponents equal to one another and solving for x x :
Using the One-to-One Property of Exponential Functions to Solve Exponential Equations
For any algebraic expressions S and T , S and T , and any positive real number b ≠ 1 , b ≠ 1 ,
Given an exponential equation with the form b S = b T , b S = b T , where S S and T T are algebraic expressions with an unknown, solve for the unknown.
- Use the rules of exponents to simplify, if necessary, so that the resulting equation has the form b S = b T . b S = b T .
- Use the one-to-one property to set the exponents equal.
- Solve the resulting equation, S = T , S = T , for the unknown.
Solving an Exponential Equation with a Common Base
Solve 2 x − 1 = 2 2 x − 4 . 2 x − 1 = 2 2 x − 4 .
Solve 5 2 x = 5 3 x + 2 . 5 2 x = 5 3 x + 2 .
Rewriting Equations So All Powers Have the Same Base
Sometimes the common base for an exponential equation is not explicitly shown. In these cases, we simply rewrite the terms in the equation as powers with a common base, and solve using the one-to-one property.
For example, consider the equation 256 = 4 x − 5 . 256 = 4 x − 5 . We can rewrite both sides of this equation as a power of 2. 2. Then we apply the rules of exponents, along with the one-to-one property, to solve for x : x :
Given an exponential equation with unlike bases, use the one-to-one property to solve it.
- Rewrite each side in the equation as a power with a common base.
Solving Equations by Rewriting Them to Have a Common Base
Solve 8 x + 2 = 16 x + 1 . 8 x + 2 = 16 x + 1 .
Solve 5 2 x = 25 3 x + 2 . 5 2 x = 25 3 x + 2 .
Solving Equations by Rewriting Roots with Fractional Exponents to Have a Common Base
Solve 2 5 x = 2 . 2 5 x = 2 .
Solve 5 x = 5 . 5 x = 5 .
Do all exponential equations have a solution? If not, how can we tell if there is a solution during the problem-solving process?
No. Recall that the range of an exponential function is always positive. While solving the equation, we may obtain an expression that is undefined.
Solving an Equation with Positive and Negative Powers
Solve 3 x + 1 = −2. 3 x + 1 = −2.
This equation has no solution. There is no real value of x x that will make the equation a true statement because any power of a positive number is positive.
Figure 2 shows that the two graphs do not cross so the left side is never equal to the right side. Thus the equation has no solution.
Solve 2 x = −100. 2 x = −100.
Solving Exponential Equations Using Logarithms
Sometimes the terms of an exponential equation cannot be rewritten with a common base. In these cases, we solve by taking the logarithm of each side. Recall, since log ( a ) = log ( b ) log ( a ) = log ( b ) is equivalent to a = b , a = b , we may apply logarithms with the same base on both sides of an exponential equation.
Given an exponential equation in which a common base cannot be found, solve for the unknown.
- If one of the terms in the equation has base 10, use the common logarithm.
- If none of the terms in the equation has base 10, use the natural logarithm.
- Use the rules of logarithms to solve for the unknown.
Solving an Equation Containing Powers of Different Bases
Solve 5 x + 2 = 4 x . 5 x + 2 = 4 x .
Solve 2 x = 3 x + 1 . 2 x = 3 x + 1 .
Is there any way to solve 2 x = 3 x ? 2 x = 3 x ?
Yes. The solution is 0. 0.
Equations Containing e
One common type of exponential equations are those with base e . e . This constant occurs again and again in nature, in mathematics, in science, in engineering, and in finance. When we have an equation with a base e e on either side, we can use the natural logarithm to solve it.
Given an equation of the form y = A e k t , y = A e k t , solve for t . t .
- Divide both sides of the equation by A . A .
- Apply the natural logarithm of both sides of the equation.
- Divide both sides of the equation by k . k .
Solve an Equation of the Form y = Ae kt
Solve 100 = 20 e 2 t . 100 = 20 e 2 t .
Using laws of logs, we can also write this answer in the form t = ln 5 . t = ln 5 . If we want a decimal approximation of the answer, we use a calculator.
Solve 3 e 0.5 t = 11. 3 e 0.5 t = 11.
Does every equation of the form y = A e k t y = A e k t have a solution?
No. There is a solution when k ≠ 0 , k ≠ 0 , and when y y and A A are either both 0 or neither 0, and they have the same sign. An example of an equation with this form that has no solution is 2 = −3 e t . 2 = −3 e t .
Solving an Equation That Can Be Simplified to the Form y = Ae kt
Solve 4 e 2 x + 5 = 12. 4 e 2 x + 5 = 12.
Solve 3 + e 2 t = 7 e 2 t . 3 + e 2 t = 7 e 2 t .
Extraneous Solutions
Sometimes the methods used to solve an equation introduce an extraneous solution , which is a solution that is correct algebraically but does not satisfy the conditions of the original equation. One such situation arises in solving when the logarithm is taken on both sides of the equation. In such cases, remember that the argument of the logarithm must be positive. If the number we are evaluating in a logarithm function is negative, there is no output.
Solving Exponential Functions in Quadratic Form
Solve e 2 x − e x = 56. e 2 x − e x = 56.
When we plan to use factoring to solve a problem, we always get zero on one side of the equation, because zero has the unique property that when a product is zero, one or both of the factors must be zero. We reject the equation e x = −7 e x = −7 because a positive number never equals a negative number. The solution ln ( −7 ) ln ( −7 ) is not a real number, and in the real number system this solution is rejected as an extraneous solution.
Solve e 2 x = e x + 2. e 2 x = e x + 2.
Does every logarithmic equation have a solution?
No. Keep in mind that we can only apply the logarithm to a positive number. Always check for extraneous solutions.
Using the Definition of a Logarithm to Solve Logarithmic Equations
We have already seen that every logarithmic equation log b ( x ) = y log b ( x ) = y is equivalent to the exponential equation b y = x . b y = x . We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.
For example, consider the equation log 2 ( 2 ) + log 2 ( 3 x − 5 ) = 3. log 2 ( 2 ) + log 2 ( 3 x − 5 ) = 3. To solve this equation, we can use rules of logarithms to rewrite the left side in compact form and then apply the definition of logs to solve for x : x :
For any algebraic expression S S and real numbers b b and c , c , where b > 0 , b ≠ 1 , b > 0 , b ≠ 1 ,
Using Algebra to Solve a Logarithmic Equation
Solve 2 ln x + 3 = 7. 2 ln x + 3 = 7.
Solve 6 + ln x = 10. 6 + ln x = 10.
Using Algebra Before and After Using the Definition of the Natural Logarithm
Solve 2 ln ( 6 x ) = 7. 2 ln ( 6 x ) = 7.
Solve 2 ln ( x + 1 ) = 10. 2 ln ( x + 1 ) = 10.
Using a Graph to Understand the Solution to a Logarithmic Equation
Solve ln x = 3. ln x = 3.
Figure 3 represents the graph of the equation. On the graph, the x -coordinate of the point at which the two graphs intersect is close to 20. In other words e 3 ≈ 20. e 3 ≈ 20. A calculator gives a better approximation: e 3 ≈ 20.0855. e 3 ≈ 20.0855.
Use a graphing calculator to estimate the approximate solution to the logarithmic equation 2 x = 1000 2 x = 1000 to 2 decimal places.
Using the One-to-One Property of Logarithms to Solve Logarithmic Equations
As with exponential equations, we can use the one-to-one property to solve logarithmic equations. The one-to-one property of logarithmic functions tells us that, for any real numbers x > 0 , x > 0 , S > 0 , S > 0 , T > 0 T > 0 and any positive real number b , b , where b ≠ 1 , b ≠ 1 ,
For example,
So, if x − 1 = 8 , x − 1 = 8 , then we can solve for x , x , and we get x = 9. x = 9. To check, we can substitute x = 9 x = 9 into the original equation: log 2 ( 9 − 1 ) = log 2 ( 8 ) = 3. log 2 ( 9 − 1 ) = log 2 ( 8 ) = 3. In other words, when a logarithmic equation has the same base on each side, the arguments must be equal. This also applies when the arguments are algebraic expressions. Therefore, when given an equation with logs of the same base on each side, we can use rules of logarithms to rewrite each side as a single logarithm. Then we use the fact that logarithmic functions are one-to-one to set the arguments equal to one another and solve for the unknown.
For example, consider the equation log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) . log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) . To solve this equation, we can use the rules of logarithms to rewrite the left side as a single logarithm, and then apply the one-to-one property to solve for x : x :
To check the result, substitute x = 10 x = 10 into log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) . log ( 3 x − 2 ) − log ( 2 ) = log ( x + 4 ) .
For any algebraic expressions S S and T T and any positive real number b , b , where b ≠ 1 , b ≠ 1 ,
Note, when solving an equation involving logarithms, always check to see if the answer is correct or if it is an extraneous solution.
Given an equation containing logarithms, solve it using the one-to-one property.
- Use the rules of logarithms to combine like terms, if necessary, so that the resulting equation has the form log b S = log b T . log b S = log b T .
- Use the one-to-one property to set the arguments equal.
Solving an Equation Using the One-to-One Property of Logarithms
Solve ln ( x 2 ) = ln ( 2 x + 3 ) . ln ( x 2 ) = ln ( 2 x + 3 ) .
There are two solutions: 3 3 or −1. −1. The solution −1 −1 is negative, but it checks when substituted into the original equation because the argument of the logarithm functions is still positive.
Solve ln ( x 2 ) = ln 1. ln ( x 2 ) = ln 1.
Solving Applied Problems Using Exponential and Logarithmic Equations
In previous sections, we learned the properties and rules for both exponential and logarithmic functions. We have seen that any exponential function can be written as a logarithmic function and vice versa. We have used exponents to solve logarithmic equations and logarithms to solve exponential equations. We are now ready to combine our skills to solve equations that model real-world situations, whether the unknown is in an exponent or in the argument of a logarithm.
One such application is in science, in calculating the time it takes for half of the unstable material in a sample of a radioactive substance to decay, called its half-life . Table 1 lists the half-life for several of the more common radioactive substances.
We can see how widely the half-lives for these substances vary. Knowing the half-life of a substance allows us to calculate the amount remaining after a specified time. We can use the formula for radioactive decay:
- A 0 A 0 is the amount initially present
- T T is the half-life of the substance
- t t is the time period over which the substance is studied
- A ( t ) A ( t ) is the amount of the substance present after time t t
Using the Formula for Radioactive Decay to Find the Quantity of a Substance
How long will it take for ten percent of a 1000-gram sample of uranium-235 to decay?
Ten percent of 1000 grams is 100 grams. If 100 grams decay, the amount of uranium-235 remaining is 900 grams.
How long will it take before twenty percent of our 1000-gram sample of uranium-235 has decayed?
Access these online resources for additional instruction and practice with exponential and logarithmic equations.
- Solving Logarithmic Equations
- Solving Exponential Equations with Logarithms
6.6 Section Exercises
How can an exponential equation be solved?
When does an extraneous solution occur? How can an extraneous solution be recognized?
When can the one-to-one property of logarithms be used to solve an equation? When can it not be used?
For the following exercises, use like bases to solve the exponential equation.
4 − 3 v − 2 = 4 − v 4 − 3 v − 2 = 4 − v
64 ⋅ 4 3 x = 16 64 ⋅ 4 3 x = 16
3 2 x + 1 ⋅ 3 x = 243 3 2 x + 1 ⋅ 3 x = 243
2 − 3 n ⋅ 1 4 = 2 n + 2 2 − 3 n ⋅ 1 4 = 2 n + 2
625 ⋅ 5 3 x + 3 = 125 625 ⋅ 5 3 x + 3 = 125
36 3 b 36 2 b = 216 2 − b 36 3 b 36 2 b = 216 2 − b
( 1 64 ) 3 n ⋅ 8 = 2 6 ( 1 64 ) 3 n ⋅ 8 = 2 6
For the following exercises, use logarithms to solve.
9 x − 10 = 1 9 x − 10 = 1
2 e 6 x = 13 2 e 6 x = 13
e r + 10 − 10 = −42 e r + 10 − 10 = −42
2 ⋅ 10 9 a = 29 2 ⋅ 10 9 a = 29
− 8 ⋅ 10 p + 7 − 7 = −24 − 8 ⋅ 10 p + 7 − 7 = −24
7 e 3 n − 5 + 5 = −89 7 e 3 n − 5 + 5 = −89
e − 3 k + 6 = 44 e − 3 k + 6 = 44
− 5 e 9 x − 8 − 8 = −62 − 5 e 9 x − 8 − 8 = −62
− 6 e 9 x + 8 + 2 = −74 − 6 e 9 x + 8 + 2 = −74
2 x + 1 = 5 2 x − 1 2 x + 1 = 5 2 x − 1
e 2 x − e x − 132 = 0 e 2 x − e x − 132 = 0
7 e 8 x + 8 − 5 = −95 7 e 8 x + 8 − 5 = −95
10 e 8 x + 3 + 2 = 8 10 e 8 x + 3 + 2 = 8
4 e 3 x + 3 − 7 = 53 4 e 3 x + 3 − 7 = 53
8 e − 5 x − 2 − 4 = −90 8 e − 5 x − 2 − 4 = −90
3 2 x + 1 = 7 x − 2 3 2 x + 1 = 7 x − 2
e 2 x − e x − 6 = 0 e 2 x − e x − 6 = 0
3 e 3 − 3 x + 6 = −31 3 e 3 − 3 x + 6 = −31
For the following exercises, use the definition of a logarithm to rewrite the equation as an exponential equation.
log ( 1 100 ) = −2 log ( 1 100 ) = −2
log 324 ( 18 ) = 1 2 log 324 ( 18 ) = 1 2
For the following exercises, use the definition of a logarithm to solve the equation.
5 log 7 n = 10 5 log 7 n = 10
− 8 log 9 x = 16 − 8 log 9 x = 16
4 + log 2 ( 9 k ) = 2 4 + log 2 ( 9 k ) = 2
2 log ( 8 n + 4 ) + 6 = 10 2 log ( 8 n + 4 ) + 6 = 10
10 − 4 ln ( 9 − 8 x ) = 6 10 − 4 ln ( 9 − 8 x ) = 6
For the following exercises, use the one-to-one property of logarithms to solve.
ln ( 10 − 3 x ) = ln ( − 4 x ) ln ( 10 − 3 x ) = ln ( − 4 x )
log 13 ( 5 n − 2 ) = log 13 ( 8 − 5 n ) log 13 ( 5 n − 2 ) = log 13 ( 8 − 5 n )
log ( x + 3 ) − log ( x ) = log ( 74 ) log ( x + 3 ) − log ( x ) = log ( 74 )
ln ( − 3 x ) = ln ( x 2 − 6 x ) ln ( − 3 x ) = ln ( x 2 − 6 x )
log 4 ( 6 − m ) = log 4 3 m log 4 ( 6 − m ) = log 4 3 m
ln ( x − 2 ) − ln ( x ) = ln ( 54 ) ln ( x − 2 ) − ln ( x ) = ln ( 54 )
log 9 ( 2 n 2 − 14 n ) = log 9 ( − 45 + n 2 ) log 9 ( 2 n 2 − 14 n ) = log 9 ( − 45 + n 2 )
ln ( x 2 − 10 ) + ln ( 9 ) = ln ( 10 ) ln ( x 2 − 10 ) + ln ( 9 ) = ln ( 10 )
For the following exercises, solve each equation for x . x .
log ( x + 12 ) = log ( x ) + log ( 12 ) log ( x + 12 ) = log ( x ) + log ( 12 )
ln ( x ) + ln ( x − 3 ) = ln ( 7 x ) ln ( x ) + ln ( x − 3 ) = ln ( 7 x )
log 2 ( 7 x + 6 ) = 3 log 2 ( 7 x + 6 ) = 3
ln ( 7 ) + ln ( 2 − 4 x 2 ) = ln ( 14 ) ln ( 7 ) + ln ( 2 − 4 x 2 ) = ln ( 14 )
log 8 ( x + 6 ) − log 8 ( x ) = log 8 ( 58 ) log 8 ( x + 6 ) − log 8 ( x ) = log 8 ( 58 )
ln ( 3 ) − ln ( 3 − 3 x ) = ln ( 4 ) ln ( 3 ) − ln ( 3 − 3 x ) = ln ( 4 )
log 3 ( 3 x ) − log 3 ( 6 ) = log 3 ( 77 ) log 3 ( 3 x ) − log 3 ( 6 ) = log 3 ( 77 )
For the following exercises, solve the equation for x , x , if there is a solution . Then graph both sides of the equation, and observe the point of intersection (if it exists) to verify the solution.
log 9 ( x ) − 5 = −4 log 9 ( x ) − 5 = −4
log 3 ( x ) + 3 = 2 log 3 ( x ) + 3 = 2
ln ( 3 x ) = 2 ln ( 3 x ) = 2
ln ( x − 5 ) = 1 ln ( x − 5 ) = 1
log ( 4 ) + log ( − 5 x ) = 2 log ( 4 ) + log ( − 5 x ) = 2
− 7 + log 3 ( 4 − x ) = −6 − 7 + log 3 ( 4 − x ) = −6
ln ( 4 x − 10 ) − 6 = − 5 ln ( 4 x − 10 ) − 6 = − 5
log ( 4 − 2 x ) = log ( − 4 x ) log ( 4 − 2 x ) = log ( − 4 x )
log 11 ( − 2 x 2 − 7 x ) = log 11 ( x − 2 ) log 11 ( − 2 x 2 − 7 x ) = log 11 ( x − 2 )
ln ( 2 x + 9 ) = ln ( − 5 x ) ln ( 2 x + 9 ) = ln ( − 5 x )
log 9 ( 3 − x ) = log 9 ( 4 x − 8 ) log 9 ( 3 − x ) = log 9 ( 4 x − 8 )
log ( x 2 + 13 ) = log ( 7 x + 3 ) log ( x 2 + 13 ) = log ( 7 x + 3 )
3 log 2 ( 10 ) − log ( x − 9 ) = log ( 44 ) 3 log 2 ( 10 ) − log ( x − 9 ) = log ( 44 )
ln ( x ) − ln ( x + 3 ) = ln ( 6 ) ln ( x ) − ln ( x + 3 ) = ln ( 6 )
For the following exercises, solve for the indicated value, and graph the situation showing the solution point.
An account with an initial deposit of $6,500 $6,500 earns 7.25 % 7.25 % annual interest, compounded continuously. How much will the account be worth after 20 years?
The formula for measuring sound intensity in decibels D D is defined by the equation D = 10 log ( I I 0 ) , D = 10 log ( I I 0 ) , where I I is the intensity of the sound in watts per square meter and I 0 = 10 − 12 I 0 = 10 − 12 is the lowest level of sound that the average person can hear. How many decibels are emitted from a jet plane with a sound intensity of 8.3 ⋅ 10 2 8.3 ⋅ 10 2 watts per square meter?
The population of a small town is modeled by the equation P = 1650 e 0.5 t P = 1650 e 0.5 t where t t is measured in years. In approximately how many years will the town’s population reach 20,000? 20,000?
For the following exercises, solve each equation by rewriting the exponential expression using the indicated logarithm. Then use a calculator to approximate the variable to 3 decimal places.
1000 ( 1.03 ) t = 5000 1000 ( 1.03 ) t = 5000 using the common log.
e 5 x = 17 e 5 x = 17 using the natural log
3 ( 1.04 ) 3 t = 8 3 ( 1.04 ) 3 t = 8 using the common log
3 4 x − 5 = 38 3 4 x − 5 = 38 using the common log
50 e − 0.12 t = 10 50 e − 0.12 t = 10 using the natural log
For the following exercises, use a calculator to solve the equation. Unless indicated otherwise, round all answers to the nearest ten-thousandth.
7 e 3 x − 5 + 7.9 = 47 7 e 3 x − 5 + 7.9 = 47
ln ( 3 ) + ln ( 4.4 x + 6.8 ) = 2 ln ( 3 ) + ln ( 4.4 x + 6.8 ) = 2
log ( − 0.7 x − 9 ) = 1 + 5 log ( 5 ) log ( − 0.7 x − 9 ) = 1 + 5 log ( 5 )
Atmospheric pressure P P in pounds per square inch is represented by the formula P = 14.7 e − 0.21 x , P = 14.7 e − 0.21 x , where x x is the number of miles above sea level. To the nearest foot, how high is the peak of a mountain with an atmospheric pressure of 8.369 8.369 pounds per square inch? ( Hint : there are 5280 feet in a mile)
The magnitude M of an earthquake is represented by the equation M = 2 3 log ( E E 0 ) M = 2 3 log ( E E 0 ) where E E is the amount of energy released by the earthquake in joules and E 0 = 10 4.4 E 0 = 10 4.4 is the assigned minimal measure released by an earthquake. To the nearest hundredth, what would the magnitude be of an earthquake releasing 1.4 ⋅ 10 13 1.4 ⋅ 10 13 joules of energy?
Use the definition of a logarithm along with the one-to-one property of logarithms to prove that b log b x = x . b log b x = x .
Recall the formula for continually compounding interest, y = A e k t . y = A e k t . Use the definition of a logarithm along with properties of logarithms to solve the formula for time t t such that t t is equal to a single logarithm.
Recall the compound interest formula A = a ( 1 + r k ) k t . A = a ( 1 + r k ) k t . Use the definition of a logarithm along with properties of logarithms to solve the formula for time t . t .
Newton’s Law of Cooling states that the temperature T T of an object at any time t can be described by the equation T = T s + ( T 0 − T s ) e − k t , T = T s + ( T 0 − T s ) e − k t , where T s T s is the temperature of the surrounding environment, T 0 T 0 is the initial temperature of the object, and k k is the cooling rate. Use the definition of a logarithm along with properties of logarithms to solve the formula for time t t such that t t is equal to a single logarithm.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: College Algebra 2e
- Publication date: Dec 21, 2021
- Location: Houston, Texas
- Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/college-algebra-2e/pages/6-6-exponential-and-logarithmic-equations
© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Choose Your Test
Sat / act prep online guides and tips, the 11 natural log rules you need to know.
Other High School

If you're taking a high school or college math class, you'll likely cover natural logs. But what are natural logs? What is ln? Why does the letter e keep showing up?
Natural logs may seem difficult, but once you understand a few key natural log rules, you'll be able to easily solve even very complicated-looking problems. In this guide, we explain the four most important natural logarithm rules, discuss other natural log properties you should know, go over several examples of varying difficulty, and explain how natural logs differ from other logarithms.
What Is ln?
The natural log, or ln, is the inverse of e . The letter ‘ e' represents a mathematical constant also known as the natural exponent. Like π, e is a mathematical constant and has a set value. The value of e is equal to approximately 2.71828.
e appears in many instances in mathematics, including scenarios about compound interest, growth equations, and decay equations. ln( x ) is the time needed to grow to x , while e x is the amount of growth that has occurred after time x .
Because e is used so commonly in math and economics, and people in these fields often need to take the logarithm with a base of e of a number to solve an equation or find a value, the natural log was created as a shortcut way to write and calculate log base e . The natural log simply lets people reading the problem know that you're taking the logarithm, with a base of e , of a number. So ln( x ) = log e ( x ). As an example, ln( 5 ) = log e ( 5 ) = 1.609.
The 4 Key Natural Log Rules
There are four main rules you need to know when working with natural logs, and you'll see each of them again and again in your math problems. Know these well because they can be confusing the first time you see them, and you want to make sure you have basic rules like these down solid before moving on to more difficult logarithm topics.
Product Rule
- ln(x)(y) = ln(x) + ln(y)
- The natural log of the multiplication of x and y is the sum of the ln of x and ln of y.
- Example: ln(8)(6) = ln(8) + ln(6)

Quotient Rule
- ln(x/y) = ln(x) - ln(y)
- The natural log of the division of x and y is the difference of the ln of x and ln of y.
- Example: ln(7/4) = ln(7) - ln(4)
Reciprocal Rule
- ln(1/x) = −ln(x)
- The natural log of the reciprocal of x is the opposite of the ln of x.
- Example: ln(⅓)= -ln(3)
- ln( x y ) = y * ln(x)
- The natural log of x raised to the power of y is y times the ln of x.
- Example: ln(5 2 ) = 2 * ln(5)
Key Natural Log Properties
In addition to the four natural logarithm rules discussed above, there are also several ln properties you need to know if you're studying natural logs. Have these memorized so you can quickly move onto the next step of the problem without wasting time trying to remember common ln properties.
As you can see from the final three rows, ln( e )=1, and this is true even if one is raised to the power of the other. This is because the ln and e are inverse functions of each other.
Natural Log Sample Problems
Now it's time to put your skills to the test and ensure you understand the ln rules by applying them to example problems. Below are three sample problems. Try to work them out on your own before reading through the explanation.
Evaluate ln(7 2 /5)
First, we use the quotient rule to get: ln(7 2 ) - ln(5).
Next, we use the power rule to get: 2ln(7) -ln(5).
If you don't have a calculator, you can leave the equation like this, or you can calculate the natural log values: 2(1.946) - 1.609 = 3.891 - 1.609 = 2.282.
Evaluate ln( e ) /7
For this problem, we need to remember than ln( e )=1
This means the problem simplifies to 1/7, which is our answer
Solve ln (5 x -6)=2
When you have multiple variables within the ln parentheses, you want to make e the base and everything else the exponent of e . Then you'll get ln and e next to each other and, as we know from the natural log rules, e ln(x) =x.
So, the equation becomes e ln(5x-6) = e 2
Since e ln(x) = x , e ln(5x-6) = 5x-6
Therefore 5 x -6= e 2
Since e is a constant, you can then figure out the value of e 2 , either by using the e key on your calculator or using e's estimated value of 2.718.
5 x -6 =7.389
Now we'd add 6 to both sides
5 x = 13.389
Finally, we'd divide both sides by 5.
How Are Natural Logs Different From Other Logarithms?
As a reminder, a logarithm is the opposite of a power. If you take the log of a number, you're undoing the exponent. The key difference between natural logs and other logarithms is the base being used. Logarithms typically use a base of 10 (although it can be a different value, which will be specified), while natural logs will always use a base of e .
This means ln(x)=log e ( x )
If you need to convert between logarithms and natural logs, use the following two equations:
- log 10 ( x ) = ln(x) / ln(10)
- ln(x) = log 10 ( x ) / log 10 ( e )
Other than the difference in the base (which is a big difference) the logarithm rules and the natural logarithm rules are the same:
Summary: Natural Log Rules
The natural log, or ln, is the inverse of e. The rules of natural logs may seem counterintuitive at first, but once you learn them they're quite simple to remember and apply to practice problems.
The four main ln rules are:
- ln(x)( y) = ln(x) + ln(y)
- ln(1/x)=−ln(x)
- n( x y ) = y*ln(x)
The key difference between natural logs and other logarithms is the base being used.
What's Next?
Writing a research paper for school but not sure what to write about? Our guide to research paper topics has over 100 topics in ten categories so you can be sure to find the perfect topic for you.
Want to know the fastest and easiest ways to convert between Fahrenheit and Celsius? We've got you covered! Check out our guide to the best ways to convert Celsius to Fahrenheit (or vice versa).
Taking the SAT or ACT? Students often struggle most with the Math section of these tests, but check out our comprehensive guides to SAT Math and ACT Math for everything you need to know to ace these math questions.

Christine graduated from Michigan State University with degrees in Environmental Biology and Geography and received her Master's from Duke University. In high school she scored in the 99th percentile on the SAT and was named a National Merit Finalist. She has taught English and biology in several countries.
Ask a Question Below
Have any questions about this article or other topics? Ask below and we'll reply!
Improve With Our Famous Guides
- For All Students
The 5 Strategies You Must Be Using to Improve 160+ SAT Points
How to Get a Perfect 1600, by a Perfect Scorer
Series: How to Get 800 on Each SAT Section:
Score 800 on SAT Math
Score 800 on SAT Reading
Score 800 on SAT Writing
Series: How to Get to 600 on Each SAT Section:
Score 600 on SAT Math
Score 600 on SAT Reading
Score 600 on SAT Writing
Free Complete Official SAT Practice Tests
What SAT Target Score Should You Be Aiming For?
15 Strategies to Improve Your SAT Essay
The 5 Strategies You Must Be Using to Improve 4+ ACT Points
How to Get a Perfect 36 ACT, by a Perfect Scorer
Series: How to Get 36 on Each ACT Section:
36 on ACT English
36 on ACT Math
36 on ACT Reading
36 on ACT Science
Series: How to Get to 24 on Each ACT Section:
24 on ACT English
24 on ACT Math
24 on ACT Reading
24 on ACT Science
What ACT target score should you be aiming for?
ACT Vocabulary You Must Know
ACT Writing: 15 Tips to Raise Your Essay Score
How to Get Into Harvard and the Ivy League
How to Get a Perfect 4.0 GPA
How to Write an Amazing College Essay
What Exactly Are Colleges Looking For?
Is the ACT easier than the SAT? A Comprehensive Guide
Should you retake your SAT or ACT?
When should you take the SAT or ACT?
Stay Informed
Get the latest articles and test prep tips!
Looking for Graduate School Test Prep?
Check out our top-rated graduate blogs here:
GRE Online Prep Blog
GMAT Online Prep Blog
TOEFL Online Prep Blog
Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

3.4.2: Common and Natural Logarithms
- Last updated
- Save as PDF
- Page ID 14377
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Common and Natural Logarithms
By now, you know that log 2 64=x can be solved if you recognize that 2 6 =64. What about numbers that aren't so 'clean'? There aren't many people who could calculate the answer to log 7 247=x in their head! It would be great to use a calculator, but most only have two log functions: base 10 and base e .
Is there a way to convert from one base to another, so we can use a calculator?
Although a log function can have any positive number as a base, there are really only two bases that are commonly used in the real world. Both may be written without a base noted, like: logx, so you may need to use the context to decide which is appropriate.
The common log is a log with base 10. It is used to define pH, earthquake magnitude, and sound decibel levels, among many many other common real-world values.
The natural log , sometimes written ln(x), is a log with base e . The transcendental number e is approximately 2.71828 and is used in any number of calculations involving constant growth in chemistry, physics, biology, finance, etc..
Using a Calculator for logs
You may have noticed that the common log and the natural log are the only log buttons on your calculator. We can use either the common log or the natural log to find the values of logs with other bases.
The equation \(\ \log _{b} x=\frac{\log x}{\log b}\) is called the change of base formula, and may be used to convert to common log or natural log .
You may also see the change of base formula as \(\ \log _{b} x=\frac{\ln x}{\ln b}\), which is the same formula specifying a conversion to the natural log .
Using the change of base formula, we can find the common log (or the natural log) equivalent of any other base so that we can use a calculator to find the value of an expression.
Consider log 3 35. If we use the change of base formula to convert to base 10, and then the log button on a calculator, we find that \(\ \log _{3} 35=\frac{\log 35}{\log 3}=3.23621727\).
Earlier, you were asked to solve the following problem: \(\ \log _{7} 247=x\)
Using the change of base formula: \(\ \log _{7} 247=\frac{\log 247}{\log 7}\)
Using a calculator to find the common logs of 247 and 7, we get (approximately) \(\ \frac{2.4}{.8}=2.8313\).
We can verify with \(\ 7^{2.8313}=247\)
\(\ \therefore \log _{7} 247=2.8313\)
Evaluate each log.
Remember that logx (with no base specified) commonly refers to log 10 x.
- \(\ \log 1\)
- \(\ \log 10\)
- \(\ \log \sqrt{10}\)
- \(\ \log 1=0 \text { because } 10^{0}=1\)
- \(\ \log 10=1 \text { because } 10^{1}=10\)
- \(\ \log \sqrt{10}=\frac{1}{2} \text { because } \sqrt{10}=10^{1 / 2}\)
For each log value, determine two integers between which the log value should lie. Then use a calculator to find the value of the log.
- \(\ \log 50\)
- \(\ \log 818\)
Using a calculator, you should find that log 50 ≈ 1.698970004.
Using a calculator, you should find that log 818 ≈ 2.912753304.
Estimate the value, and then use the change of base formula to find the value of \(\ \log _{2} 17\).
\(\ \log _{2} 17\) is close to 4 because 2 4 =16 and 2 5 =32.
Using the change of base formula, we have \(\ \log _{2} 17=\frac{\log 17}{\log 2}\).
Using a calculator, you should find that the approximate value of this expression is 4.087462841.
Find the value of each natural log.
- \(\ \ln 100\)
- \(\ \ln \sqrt{e}\)
3^{4}=81 \text { and } 3^{5}=243
Using a calculator, you should find that \(\ \ln 100=4.605171086\)
Therefore \(\ \ln \sqrt{e}=\ln \left(e^{1 / 2}\right)=1 / 2\)
Solve the equation: \(\ 5^{x}=3 \cdot 7^{x}\)
To solve: \(\ 3^{x}\left(2^{3 x}\right)=7\left(5^{x}\right)\)
\(\ 3^{x}\left(2^{3}\right)^{x}=7\left(5^{x}\right)\): Rule of exponents \(\ \left(x^{y}\right)^{z}=x^{y z}\)
\(\ 3^{x}\left(8^{x}\right)=7\left(5^{x}\right) \rightarrow 24^{x}=7\left(5^{x}\right)\): By multiplication
\(\ \left(\frac{24}{5}\right)^{x}=7\): Divide both sides by \(\ 5^x\)
\(\ \log \left(\frac{24}{5}\right)^{x}=\log 7\): Take the log of both sides
\(\ x \log \left(\frac{24}{5}\right)=\log 7\): Using \(\ \log x^{y}=y \log x\)
\(\ x=\frac{\log 7}{\log \frac{24}{5}}\): Divide both sides by \(\ \log \left(\frac{24}{5}\right)\)
\(\ x=1.24\): With a calculator
Find the value: \(\ \ln 6+\ln 7\)
Use a calculator to find the values:
\(\ \ln 6=1.79175 \text { and } \ln 7=1.94591\)
1.79175 + 1.94591 = 3.73766
- What is a common logarithm ? Where are common logs most commonly used?
- What is a natural logarithm ? Where are natural logs commonly used?
Evaluate each expression:
- \(\ \log \frac{17^{4}}{5}\)
- \(\ \log 7\left(4^{3}\right)\)
Convert to a common logarithm and evaluate:
- \(\ \log _{6} 832\)
- \(\ \log _{11} 47\)
- \(\ \log _{3} 9\)
Convert to a natural logarithm and evaluate:
- \(\ \log _{7} 91\)
- \(\ \log_5256\)
- \(\ \log_90.712\)
Find the values of the natural logarithms:
- \(\ \ln56\)
- \(\ \ln2000\)
- \(\ \ln950.1\)
- \(\ \ln.9\)
Convert the natural logs to exponential form, and solve.
- If \(\ \text { lne }=x \text { and } e^{x}=e \text { then } x=?\)
- If \(\ \ln e^{5} \text { then } x=?\)
- If \(\ \ln e^{a}=x \text { then } x=?\)
- If \(\ \ln e^{-3}=x \text { then } x=?\)
Review (Answers)
To see the Review answers, open this PDF file and look for section 3.8.

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

3.5: Properties and applications of logarithmic functions
- Last updated
- Save as PDF
- Page ID 89296

- Matthew Boelkins, David Austin & Steven Schlicker
- Grand Valley State University via ScholarWorks @Grand Valley State University
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Motivating Questions
- What structural rules do logarithms obey that are similar to rules for exponents?
- What are the key properties of the graph of the natural logarithm function?
- How do logarithms enable us to solve exponential equations?
Logarithms arise as inverses of exponential functions. In addition, we have motivated their development by our desire to solve exponential equations such as \(e^k = 3\) for \(k\text{.}\) Because of the inverse relationship between exponential and logarithmic functions, there are several important properties logarithms have that are analogous to ones held by exponential functions. We will work to develop these properties and then show how they are useful in applied settings.
Preview Activity \(\PageIndex{1}\)
In the following questions, we investigate how \(\log_{10}(a \cdot b)\) can be equivalently written in terms of \(\log_{10}(a)\) and \(\log_{10}(b)\text{.}\)
by filling in the box with an appropriate expression involving \(x\) and \(y\text{.}\)
- What is the simplest possible way to write \(\log_{10}10^x\text{?}\) What about the simplest equivalent expression for \(\log_{10}10^y\text{?}\)
- Explain why each of the following three equal signs is valid in the sequence of equalities: \begin{align*} \log_{10}(10^x \cdot 10^y) &= \log_{10}(10^{x+y})\\ &= x+y\\ &= \log_{10}(10^x) + \log_{10}(10^y)\text{.} \end{align*}
- Suppose that \(a\) and \(b\) are positive real numbers, so we can think of \(a\) as \(10^x\) for some real number \(x\) and \(b\) as \(10^y\) for some real number \(y\text{.}\) That is, say that \(a = 10^x\) and \(b = 10^y\text{.}\) What does our work in (c) tell us about \(\log_{10}(ab)\text{?}\)
Key properties of logarithms
In Preview Activity \(\PageIndex{1}\) , we considered an argument for why \(\log_{10}(ab) = \log_{10}(a) + \log_{10}(b)\) for any choice of positive numbers \(a\) and \(b\text{.}\) In what follows, we develop this and other properties of the natural logarithm function; similar reasoning shows the same properties hold for logarithms of any base.
Let \(a\) and \(b\) be any positive real numbers so that \(x = \ln(a)\) and \(y = \ln(b)\) are both defined. Observe that we can rewrite these two equations using the definition of the natural logarithm so that
Using substitution, we can now say that
By exponent rules, we know that \(\ln(e^x \cdot e^y) = \ln(e^{x+y})\text{,}\) and because the natural logarithm and natural exponential function are inverses, \(\ln(e^{x+y}) = x+y\text{.}\) Combining the three most recent equations,
Finally, recalling that \(x = \ln(a)\) and \(y = \ln(b)\text{,}\) we have shown that
for any choice of positive real numbers \(a\) and \(b\text{.}\)
A similar property holds for \(\ln(\frac{a}{b})\text{.}\) By nearly the same argument, we can say that
We have thus shown the following general principles.
Logarithms of products and quotients.
For any positive real numbers \(a\) and \(b\text{,}\)
- \(\displaystyle \ln(a \cdot b) = \ln(a) + \ln(b)\)
- \(\displaystyle \ln\left( \frac{a}{b} \right) = \ln(a) - \ln(b)\)
Because positive integer exponents are a shorthand way to express repeated multiplication, we can use the multiplication rule for logarithms to think about exponents as well. For example,
and by repeated application of the rule for the natural logarithm of a product, we see
A similar argument works to show that for every natural number \(n\text{,}\)
More sophisticated mathematics can be used to prove that the following property holds for every real number exponent \(t\text{.}\)
Logarithms of exponential expressions.
For any positive real number \(a\) and any real number \(t\text{,}\)
\[ \ln(a^t) = t\ln(a)\text{.} \nonumber \]
The rule that \(\ln(a^t) = t\ln(a)\) is extremely powerful: by working with logarithms appropriately, it enables us to move from having a variable in an exponential expression to the variable being part of a linear expression. Moreover, it enables us to solve exponential equations exactly, regardless of the base involved.
Example \(\PageIndex{1}\)
Solve the equation \(7 \cdot 3^t - 1 = 5\) exactly for \(t\text{.}\)
To solve for \(t\text{,}\) we first solve for \(3^t\text{.}\) Adding \(1\) to both sides and dividing by \(7\text{,}\) we find that \(3^t = \frac{6}{7} \text{.}\) Next, we take the natural logarithm of both sides of the equation. Doing so, we have
Applying the rule for the logarithm of an exponential expression on the left, we see that \(t \ln(3) = \ln \left( \frac{6}{7} \right) \text{.}\) Both \(\ln(3)\) and \(\ln \left( \frac{6}{7} \right)\) are simply numbers, and thus we conclude that
The approach used in Example \(\PageIndex{1}\) works in a wide range of settings: any time we have an exponential equation of the form \(p \cdot q^t + r = s\text{,}\) we can solve for \(t\) by first isolating the exponential expression \(q^t\) and then by taking the natural logarithm of both sides of the equation.
Activity \(\PageIndex{2}\)
Solve each of the following equations exactly and then find an estimate that is accurate to 5 decimal places.
- \(\displaystyle 3^t = 5\)
- \(\displaystyle 4 \cdot 2^t - 2 = 3\)
- \(\displaystyle 3.7 \cdot (0.9)^{0.3t} + 1.5 = 2.1\)
- \(\displaystyle 72 - 30(0.7)^{0.05t} = 60\)
- \(\displaystyle \ln(t) = -2\)
- \(\displaystyle 3 + 2\log_{10}(t) = 3.5\)
The graph of the natural logarithm
As the inverse of the natural exponential function \(E(x) = e^x\text{,}\) we have already established that the natural logarithm \(N(x) = \ln(x)\) has the set of all positive real numbers as its domain and the set of all real numbers as its range. In addition, being the inverse of \(E(x) = e^x\text{,}\) we know that when we plot the natural logarithm and natural exponential functions on the same coordinate axes, their graphs are reflections of one another across the line \(y = x\text{,}\) as seen in Figure \(\PageIndex{2}\) and Figure \(\PageIndex{3}\)
Indeed, for any point \((a,b)\) that lies on the graph of \(E(x) = e^x\text{,}\) it follows that the point \((b,a)\) lies on the graph of the inverse \(N(x) = \ln(x)\text{.}\) From this, we see several important properties of the graph of the logarithm function.
The graph of \(y = \ln(x)\).
The graph of \(y = \ln(x)\)
- passes through the point \((1,0)\text{;}\)
- is always increasing;
- is always concave down; and
- increases without bound.
Because the graph of \(E(x) = e^x\) increases more and more rapidly as \(x\) increases, the graph of \(N(x) = \ln(x)\) increases more and more slowly as \(x\) increases. Even though the natural logarithm function grows very slowly, it does grow without bound because we can make \(\ln(x)\) as large as we want by making \(x\) sufficiently large. For instance, if we want \(x\) such that \(\ln(x) = 100\text{,}\) we choose \(x = e^{100}\text{,}\) since \(\ln(e^{100}) = 100\text{.}\)
While the natural exponential function and the natural logarithm (and transformations of these functions) are connected and have certain similar properties, it's also important to be able to distinguish between behavior that is fundamentally exponential and fundamentally logarithmic.
Activity \(\PageIndex{3}\)
In the questions that follow, we compare and contrast the properties and behaviors of exponential and logarithmic functions.
- Let \(f(t) = 1 - e^{-(t-1)}\) and \(g(t) = \ln(t)\text{.}\) Plot each function on the same set of coordinate axes. What properties do the two functions have in common? For what properties do the two functions differ? Consider each function's domain, range, \(t\)-intercept, \(y\)-intercept, increasing/decreasing behavior, concavity, and long-term behavior.
- Let \(h(t) = a - be^{-k(t-c)}\text{,}\) where \(a\text{,}\) \(b\text{,}\) \(c\text{,}\) and \(k\) are positive constants. Describe \(h\) as a transformation of the function \(E(t) = e^t\text{.}\)
- Let \(r(t) = a + b\ln(t-c)\text{,}\) where \(a\text{,}\) \(b\text{,}\) and \(c\) are positive constants. Describe \(r\) as a transformation of the function \(L(t) = \ln(t)\text{.}\)
Do you think this data is better modeled by a logarithmic function of form \(p(t) = a + b\ln(t-c)\) or by an exponential function of form \(q(t) = m + ne^{-rt}\text{.}\) Provide reasons based in how the data appears and how you think a tree grows, as well as by experimenting with sliders appropriately in Desmos . (Note: you may need to adjust the upper and lower bounds of several of the sliders in order to match the data well.)
Putting logarithms to work
We've seen in several different settings that the function \(e^{kt}\) plays a key role in modeling phenomena in the world around us. We also understand that the value of \(k\) controls whether \(e^{kt}\) is increasing (\(k \gt 0\)) or decreasing (\(k \lt 0\)) and how fast the function is increasing or decreasing. As such, we often need to determine the value of \(k\) from data that is presented to us; doing so almost always requires the use of logarithms.
Example \(\PageIndex{5}\)
A population of bacteria cells is growing at a rate proportionate to the number of cells present at a given time \(t\) (in hours). Suppose that the number of cells, \(P\text{,}\) in the population is measured in millions of cells and we know that \(P(0) = 2.475\) and \(P(10) = 4.298\text{.}\) Find a model of the form \(P(t) = Ae^{kt}\) that fits this data and use it to determine the value of \(k\) and how long it will take for the population to reach \(1\) billion cells.
Since the model has form \(P(t) = Ae^{kt}\text{,}\) we know that \(P(0) = A\text{.}\) Because we are given that \(P(0) = 2.475\text{,}\) this shows that \(A = 2.475\text{.}\) To find \(k\text{,}\) we use the fact that \(P(10) = 4.298\text{.}\) Applying this information, \(A = 2.475\text{,}\) and the form of the model, \(P(t) = Ae^{kt}\text{,}\) we see that
To solve for \(k\text{,}\) we first isolate \(e^{10k}\) by dividing both sides by \(2.475\) to get
Taking the natural logarithm of each side, we find
and thus \(k = \frac{1}{10}\ln \left( \frac{4.298}{2.475} \right) \approx 0.05519\text{.}\)
To determine how long it takes for the population to reach \(1\) billion cells, we need to solve the equation \(P(t) = 1000\text{.}\) Using our preceding work to find \(A\) and \(k\text{,}\) we know that we need to solve the equation
We divide both sides by \(2.475\) to get \(e^{\frac{1}{10}\ln \left( \frac{4.298}{2.475} \right)t} = \frac{1000}{2.475}\text{,}\) and after taking the natural logarithm of each side, we see
Activity \(\PageIndex{4}\)
Solve each of the following equations for the exact value of \(k\text{.}\)
- \(\displaystyle 41 = 50e^{-k \cdot 7}\)
- \(\displaystyle 65 = 34 + 47e^{-k \cdot 45}\)
- \(\displaystyle 7e^{2k-1} + 4 = 32\)
- \(\displaystyle \frac{5}{1+2e^{-10k}} = 4\)
For logarithms 1 , we have the following analogous structural rules for positive real numbers \(a\) and \(b\) and any real number \(t\text{:}\)
- The natural logarithm's domain is the set of all positive real numbers and its range is the set of all real numbers. Its graph passes through \((1,0)\text{,}\) is always increasing, is always concave down, and increases without bound.
where \(a\) and \(c\) are known, but \(b\) is not. In this context, we can take the natural logarithm of both sides of the equation to find that
and thus \(b\ln(a) = \ln(c)\text{,}\) so that \(b = \frac{\ln(c)}{\ln(a)}\text{.}\)
For a population that is growing exponentially according to a model of the form \(P(t) = Ae^{kt}\text{,}\) the doubling time is the amount of time that it takes the population to double. For each population described below, assume the function is growing exponentially according to a model \(P(t) = Ae^{kt}\text{,}\) where \(t\) is measured in years.
- Suppose that a certain population initially has \(100\) members and doubles after \(3\) years. What are the values of \(A\) and \(k\) in the model?
- A different population is observed to satisfy \(P(4) = 250\) and \(P(11) = 500\text{.}\) What is the population's doubling time? When will \(2000\) members of the population be present?
- Another population is observed to have doubling time \(t = 21\text{.}\) What is the value of \(k\) in the model?
- How is \(k\) related to a population's doubling time, regardless of how long the doubling time is?
A new car is purchased for $\(28000\text{.}\) Exactly \(1\) year later, the value of the car is $\(23200\text{.}\) Assume that the car's value in dollars, \(V\text{,}\) \(t\) years after purchase decays exponentially according to a model of form \(V(t) = Ae^{-kt}\text{.}\)
- Determine the exact values of \(A\) and \(k\) in the model.
- How many years will it take until the car's value is $\(10000\text{?}\)
- Suppose that rather than having the car's value decay all the way to $\(0\text{,}\) the lowest dollar amount its value ever approaches is $\(500\text{.}\) Explain why a model of the form \(V(t) = Ae^{-kt} + c\) is more appropriate.
- Under the original assumptions (\(V(0) = 28000\) and \(V(1) = 23200\)) along with the condition in (c) that the car's value will approach $\(500\) in the long-term, determine the exact values of \(A\text{,}\) \(k\text{,}\) and \(c\) in the model \(V(t) = Ae^{-kt} + c\text{.}\) Are the values of \(A\) and \(k\) the same or different from the model explored in (a)? Why?
In Exercise 3.4.5.7, we explored graphically how the function \(y = \log_b(x)\) can be thought of as a vertical stretch of the nautral logarithm, \(y = \ln(x)\text{.}\) In this exercise, we determine the exact value of the vertical stretch that is needed.
Recall that \(\log_b(x)\) is the power to which we raise \(b\) to get \(x\text{.}\)
- Write the equation \(y = \log_b(x)\) as an equivalent equation involving exponents with no logarithms present.
- Take the equation you found in (a) and take the natural logarithm of each side.
- Use rules and properties of logarithms appropriately to solve the equation from (b) for \(y\text{.}\) Your result here should express \(y\) in terms of \(\ln(x)\) and \(\ln(b)\text{.}\)
- Recall that \(y = \log_b(x)\text{.}\) Explain why the following equation (often called the Golden Rule for Logarithms) is true: \[ \log_b(x) = \frac{\ln(x)}{\ln(b)}\text{.} \nonumber \]
- What is the value of \(k\) that allows us to express the function \(y = \log_b(x)\) as a vertical stretch of the function \(y = \ln(x)\text{?}\)
Natural Log Calculator
Table of contents
The natural log calculator (or simply ln calculator) determines the logarithm to the base of a famous mathematical constant , e , an irrational number with an approximate value of e = 2.71828 . In other words, it calculates the natural logarithm.
But, what is the natural logarithm , ln x, of a given number x? This is the power the number e has to be raised to in order to result in a given number x.
How to use the natural logarithm calculator
Like all other logarithms, the natural logarithm of x returns the power, or exponent, to which a given base e must be raised to yield back the number x. It is easier to understand this notion when the base is an integer, for example, 2 or 3:
log₂ 16 = 4 since 2⁴ = 16
log₃ 81 = 4 since 3⁴ = 81
In the case of the natural logarithm, this is somewhat less intuitive because its base, e, is not an integer. But, since the value of e is between 2 and 3, we understand that e ⁴ has to be somewhere between 2⁴ = 16 and 3⁴ = 81.
It turns out that e ⁴ = 54.498 . This equality can be stated in terms of the natural logarithm in the following way, which you can check by using the ln calculator:
ln 54.498 = 4
Here are some examples of natural logarithm :
- ln 1 = 0 since e ⁰ = 1
- ln 10 = 2.3026 since e 2.3026 = 10
- ln 20 = 2.996 since e 2.996 = 20
- ln 50 = 3.912 since e 3.912 = 50
- ln 100 = 4.605 since e 4.605 = 100
You can check out the correctness of the above results by using our natural log calculator and the exponent calculator . Additionally, to better grasp the interplay between the exponential and logarithm functions , you may want to check the exponent calculator along with the log calculator .
Other ways to denote the natural logarithm
One way of denoting the natural logarithm is log e . This is the same as when we write the logarithm to the base two as log₂.
But, a more common way to write the natural logarithm is ln , which is an abbreviation of the Latin expression logarithmus naturalis, the name the natural logarithm was given when the Latin language was still the lingua franca of science.
There is also a third way of writing the natural logarithm: log . This notation is somewhat problematic, though, as it is often mistaken for the logarithm to the base 10. However, this is the syntax many software implementations of natural logarithm use, so be careful!
What's so natural about the natural logarithm?
Why exactly does ln x deserve to be called natural ? Maybe the most important property of the natural logarithm is that it is the inverse function of the exponential function eˣ , the only function whose rate of change, or the derivative , is precisely itself: ( eˣ )' = eˣ .
In simpler words, the exponential function eˣ governs its own rate of change, which in some sense makes it self-sufficient and not dependent on any other function to define the way it changes. Exactly this property makes both eˣ and its inverse function ln x the natural choice when describing many real-world phenomena .
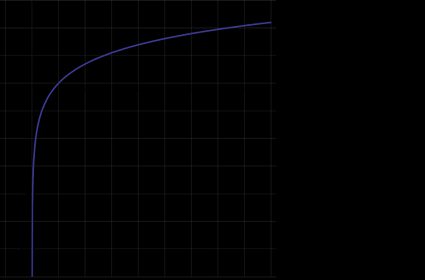
The natural log graph
Another interesting property of the natural logarithm is how it changes its values as the argument x increases. One way of expressing this is by stating that the derivative of the natural logarithm is inversely proportional to its value x, which can be written as (ln x )' = 1/ x .
You can also observe this property by looking at the graph of the natural logarithm . Although it increases as the value of x increases, the rate of growth is getting smaller and smaller as x approaches higher and higher values:
Where did the number e come from
At first glance, you wouldn't say that the number e bears any importance to the endeavors of humans or nature. But this is not so! It happens that this number is one of the most important constants in mathematics, so much so that it deserves a proper name. It is called either Euler's number or Napier's constant , depending on whom of these two great mathematicians one wants to attribute its discovery.
Nevertheless, it seems that Leonhard Euler (1707 - 1783) did get more credit, based on the fact that the very letter Euler used to denote this constant is how we denoted it today. Although Euler was the first to calculate e to a significant number of decimal places, he wasn't the first one to discover it : read more about it in the next paragraph.

How to make e amount of money
Swiss mathematician Jacob Bernoulli (1654 - 1705) stumbled upon the existence of the number e when tackling the problem of compound interest . Let us first understand the idea behind simple interest. For a given initial sum of money, say 1 USD, you want to know how much you will have after one year has passed if an interest of 100% is credited only once and at the end of the year. The answer is easy: 2 USD (you can verify it with the simple interest calculator ).

But, with compound interest, things get a bit more complicated. For example, if the same interest of 100% is now split into two equal parts of 50% and credited twice, 50% at the end of the first six months, and another 50% at the end of the year, then the final yield is obtained by using the formula
1 × (1 + 1/2)² = 2.25 USD (learn why with our compound interest calculator ).
Furthermore, if the interest of 100% is split in weekly lumps, you would have the final yield of
1 × (1 + 1/52)⁵² = 2.692 USD.
Bernoulli asked a simple question: what would happen if compounding was continuous ? In other words, what would be the final yield if the interest rate of 100% is split into infinite parts, each credited at the end of an infinitely short period of time?
This problem of continuous compound interest, stated mathematically, boils down to the challenge of calculating the limit of (1 + 1/ n ) ⁿ as n approaches infinity. It turns out that the result is precisely the number e ! Moreover, the above expression may be used as a way to define e . To answer the Bernoulli's question: with continuous compounding, the initial dollar would yield precisely e = 2.718281828 USD at the end of the year!
The real-world importance of ln 2 and other natural logarithms
The easiest natural logarithms to calculate are:
ln 1 = 0 since e ⁰ = 1 , and ln e = 1 since e ¹ = e.
But, presumably, the most important natural logarithm is the one that calculates the value of a number between 1 and e, which turns out to be the number 2. Using the natural log calculator, we get
ln 2 = 0.6931 .
It turns out that ln 2 is also equal to the alternating sum of reciprocals of all natural numbers :
ln 2 = 1 – 1/2 + 1/3 – 1/4 + 1/5 – 1/6 + ...
At first glance, this number appears to have no particular importance whatsoever. But, ln 2, as obscure as it may seem, appears in some pretty significant and, at first glance, unrelated real-world problems.
For example, it has its role in the formula for the half-life of radioactively decaying matter , as shown in our half-life calculator . It is also present in the calculation of time needed to double the initial amount of money if a fixed rate is applied over a given time.
So, if you have 1,000 USD in your bank account, and the bank provides an r = 7% per annum interest rate, you may want to ask yourself how long it will take to double my initial amount. Well, this is where ln 2 comes into play: the natural logarithm formula that calculates the time needed is (100 * ln 2)/r, which can be simplified to the approximate value of 70/r.
Therefore, in the case of r = 7%, you would get 70/7 = 10 years as an approximate time needed for your initial sum of money to double. Similarly, one can get analogous formulas for the time needed for the initial quantity to triple, quadruple, or n-tuple, given a fixed rate of growth over time.
Other applications of the natural logarithm
From the previous paragraph, we may conclude that natural logarithms occur in every process with a period-related constant growth or decay of some quantifiable phenomenon.
Apart from the already mentioned examples of radioactive decay and the problem of yield with a fixed interest rate, natural logarithms appear when calculating the growth and decay of any bacterial, animal, and plant population , the decay rates of a charged capacitor, or the temperature change of an object.
- Demystifying the Natural Logarithm
- What's so “natural” about the base of natural logarithms?
- What's the Big Deal With the Mathematical Constant e?
- David S. Kahn: Attacking Problems in Logarithms and Exponential Functions, Dover Book on Mathematics, 2015
- Edward Kasner: Mathematics and the Imagination, Dover Books on Mathematics, 2001
Natural logarithm of ...
Calculus Examples
Please ensure that your password is at least 8 characters and contains each of the following:
- a special character: @$#!%*?&

IMAGES
VIDEO
COMMENTS
Gina Wilson (All Things Algebra}, 2015 '25 -. Name: Date: Unit 7: Exponential & Logarithmic Functions Homework 3: Intro to Logarithms Directions: Write each equation in exponential form. 1. log2128 = 7 2. 64 = 2 Directions: Write each equation in logarithmic form. 25b Directions: Evaluate each logarithm. Use the change of base formula when ...
The constant e and the natural logarithm (Algebra 2 level) Learn. 𝑒 and compound interest (Opens a modal) 𝑒 as a limit (Opens a modal) Evaluating natural logarithm with calculator ... Solve exponential equations using logarithms: base-2 and other bases. 4 questions. Practice. Solving exponential models (Algebra 2 level) Learn. Exponential ...
When the exponential has base e, we use the natural logarithm. Example 10.42. Solve 3 e x + 2 = 24. 3 e x + 2 = 24. Find the exact answer and then approximate it to three decimal places. Answer : 3 e x + 2 = 24 3 e x + 2 = 24: Isolate the exponential by dividing both sides by 3. e x + 2 = 8 e x + 2 = 8: Take the natural logarithm of both sides.
The most frequently used base for logarithms is e, e, the value of which is approximately 2.71828 2.71828. Base e e logarithms are important in calculus and some scientific applications; they are called natural logarithms. The base e e logarithm, log e (x), log e (x), has its own notation, ln (x). ln (x). Most values of ln (x) ln (x) can be ...
Since the natural logarithm is a base-\(e\) logarithm, \(\ln x=\log _{e} x\), all of the properties of the logarithm apply to it. We can use the properties of the logarithm to expand logarithmic expressions using sums, differences, and coefficients. A logarithmic expression is completely expanded when the properties of the logarithm can no ...
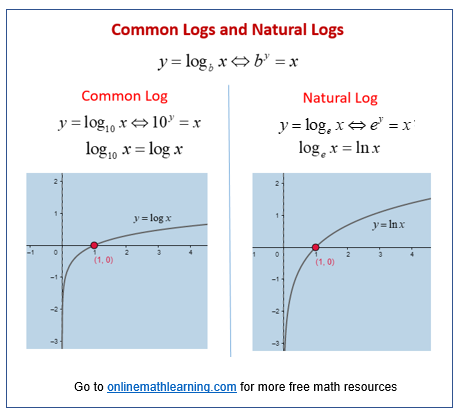
The natural logarithm has base e, a famous irrational number, and is represented on the calculator by ln (x). The natural and common logarithm can be found throughout Algebra and Calculus. The Number e and the Natural Logarithm. The natural log is the logarithm to the base of the number e and is the inverse function of an exponential function.
Exponential Function. A function that can be described by an equation of the form y= a*b^x, where b > 0 and b ≠ 1. Logarithm. The logarithm base b of a number x is the power to which b must be raised in order to equal x. This is written logb x. For example, log2 8 equals 3 since 23 = 8. Logarithmic Equation.
To solve for x , we must first isolate the exponential part. To do this, divide both sides by 5 as shown below. We do not multiply the 5 and the 2 as this goes against the order of operations! 5 ⋅ 2 x = 240 2 x = 48. Now, we can solve for x by converting the equation to logarithmic form. 2 x = 48 is equivalent to log 2.
Ln e^-4. Log e^-4. Ln 1. 0 or e^1. Ln e^8. 8. Solve for X: Ln X =. Study with Quizlet and memorize flashcards containing terms like Natural logs are the same as___ and the base is____, What is e?, (Not part of natural logs) what is the definition of b^1/2 and more.
The number e frequently occurs in mathematics (especially calculus) and is an irrational constant (like π).Its value is e = 2.718 281 828 .... Apart from logarithms to base 10 which we saw in the last section, we can also have logarithms to base e.These are called natural logarithms.. We usually write natural logarithms using `ln`, as follows: `ln x` to mean `log_e x` (that is, "`log x` to ...
3. Reduce the following expressions to simplest form. a) e 2ln3 3ln2 b) ln 1 e e c) ln 3 e e3 d) ln eS 4. Solve for x a) e xln 64 b) x c) ln 2 1 1x d) e35 10 e) ln 8 e3 x f) ln ln4 ln7x g) ln ln 2x h) eex 5 i) 1 lnx 2 j) ex 7 k) e52x 2 l) ln 4 7 4x 5. Find the solution of each equation correct to four decimal places. a) ln 1 3x b) 1 2 e x c ...
Virtual Nerd's patent-pending tutorial system provides in-context information, hints, and links to supporting tutorials, synchronized with videos, each 3 to 7 minutes long. In this non-linear system, users are free to take whatever path through the material best serves their needs. These unique features make Virtual Nerd a viable alternative to private tutoring.
The natural logarithm is a special case of the logarithm with base \(b\) in that the natural log always has base \(e\). Rather than notating the natural logarithm as \(\log_{e}(x)\) , the notation used is \(\ln (x)\). 7. No, the function has no defined value for \(x=0\) . To verify, suppose \(x=0\) is in the domain of the function \(f(x)=\log ...
If none of the terms in the equation has base 10, use the natural logarithm. Use the rules of logarithms to solve for the unknown. Example 5. Solving an Equation Containing Powers of Different Bases. ... The magnitude M of an earthquake is represented by the equation M = 2 3 log (E E 0) M = 2 3 log ...
Applications of Natural Logs and Base e Example 6: How much money will be in a bank account after 1.5 years if you invested $400 at 7.6% compounded continuously? Practice: Complete the following problems for class work.Show all work. 1. Solve ln(14x - 3) = ln(7x + 11) 2. Solve 2ex - 5 = 1 3. ln(x - 1) = -2 4.
The natural log simply lets people reading the problem know that you're taking the logarithm, with a base of e, of a number. So ln(x) = log e (x). As an example, ln(5) = log e (5) = 1.609. The 4 Key Natural Log Rules. There are four main rules you need to know when working with natural logs, and you'll see each of them again and again in your ...
In the equation, logs can be used to reduce the equation to 2x = 6 2 x = 6. 1.798982x = 1.798986 1.79898 2 x = 1.79898 6. Take the log of both sides and use the property of exponentiation of logs to bring the exponent out front. log1.798982x 2x ⋅ log 1.79898 2x x = log1.798986 = 6 ⋅ log 1.79898 = 6 = 3 log. .
)A natural logarithm is a logarithm with base . ... 3Evaluate 2ln(𝑒)+7. Homework: You should now be ready to attempt problems 5-9 in "Homework - Section 6.3" on WeBWorK. Author: Kimberly Kohnert Created Date: 1/25/2018 7:10:32 PM ...
For each log value, determine two integers between which the log value should lie. Then use a calculator to find the value of the log. \ (\ \log 50\) \ (\ \log 818\) Solution. The value of this log should be between 1 and 2, as 10 1 = 10, and 10 2 = 100. Using a calculator, you should find that log 50 ≈ 1.698970004.
Figure 3.5.3 The natural exponential and natural logarithm functions on the interval [ − 15, 15]. Indeed, for any point (a, b) that lies on the graph of E(x) = ex, it follows that the point (b, a) lies on the graph of the inverse N(x) = ln(x). From this, we see several important properties of the graph of the logarithm function.
The natural log calculator (or simply ln calculator) determines the logarithm to the base of a famous mathematical constant, e, an irrational number with an approximate value of e = 2.71828.In other words, it calculates the natural logarithm. But, what is the natural logarithm, ln x, of a given number x?This is the power the number e has to be raised to in order to result in a given number x.
• We start our discussion of natural logs with a similar basic definition: We write "log base e" as "ln" and we can define it like this: If y = ex then ln (y) = x And so, ln(ex) = x eln(x) = x • Now we have a new set of rules to add to the others: Table 4. Functions of log base 10 and base e. Exponents Log base 10 Natural Logs
The natural logarithm of e e is 1 1. 6⋅1+ln(ln(e)) 6 ⋅ 1 + ln ( ln ( e)) Multiply 6 6 by 1 1. 6+ln(ln(e)) 6 + ln ( ln ( e)) Simplify each term. Tap for more steps... Add 6 6 and 0 0. Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with step-by-step explanations, just like a ...