conclusion of mathematics assignment

Browse Course Material

Course info, instructors.

• Prof. Haynes Miller
• Dr. Nat Stapleton
• Saul Glasman

Departments

• Mathematics

As Taught In

Learning resource types, project laboratory in mathematics.

Next: Revision and Feedback »

In this section, Prof. Haynes Miller and Susan Ruff describe the criteria for good mathematical writing and the components of the writing workshop .

A central goal of the course is to teach students how to write effective, journal-style mathematics papers. Papers are a key way in which mathematicians share research findings and learn about others’ work. For each research project, each student group writes and revises a paper in the style of a professional mathematics journal paper. These research projects are perfect for helping students to learn to write as mathematicians because the students write about the new mathematics that they discover. They own it, they are committed to it, and they put a lot of effort into writing well.

Criteria for Good Writing

In the course, we help students learn to write papers that communicate clearly, follow the conventions of mathematics papers, and are mathematically engaging.

Communicating clearly is challenging for students because doing so requires writing precisely and correctly as well as anticipating readers’ needs. Although students have read textbooks and watched lectures that are worded precisely, they are often unaware of the care with which each word or piece of notation was chosen. So when students must choose the words and notation themselves, the task can be surprisingly challenging. Writing precisely is even more challenging when students write about insights they’re still developing. Even students who do a good job of writing precisely may have a different difficulty: providing sufficient groundwork for readers. When students are deeply focused on the details of their research, it can be hard for them to imagine what the reading experience may be like for someone new to that research. We can help students to communicate clearly by pointing out places within the draft at which readers may be confused by imprecise wording or by missing context.

For most students, the conventions of mathematics papers are unfamiliar because they have not read—much less written—mathematics journal papers before. The students’ first drafts often build upon their knowledge of more familiar genres: humanities papers and mathematics textbooks and lecture notes. So the text is often more verbose or explanatory than a typical paper in a mathematics journal. To help students learn the conventions of journal papers, including appropriate concision, we provide samples and individualized feedback.

Finally, a common student preconception is that mathematical writing is dry and formal, so we encourage students to write in a way that is mathematically engaging. In Spring 2013, for example, one student had to be persuaded that he did not have to use the passive voice. In reality, effective mathematics writing should be efficient and correct, but it should also provide motivation, communicate intuition, and stimulate interest.

To summarize, instruction and feedback in the course address many different aspects of successful writing:

• Precision and correctness: e.g., mathematical terminology and notation should be used correctly.
• Audience awareness: e.g., ideas should be introduced with appropriate preparation and motivation.
• Genre conventions: e.g., in most mathematics papers, the paper’s conclusion is stated in the introduction rather than in a final section titled “Conclusion.”
• Style: e.g., writing should stimulate interest.
• Other aspects of effective writing, as needed.

To help students learn to write effective mathematics papers, we provide various resources, a writing workshop, and individualized feedback on drafts.

Writing Resources

Various resources are provided to help students learn effective mathematical writing.

The following prize-winning journal article was annotated to point out various conventions and strategies of mathematical writing. (Courtesy of Mathematical Association of America. Courtesy of a Creative Commons BY-NC-SA license.)

An Annotated Journal Article (PDF)

This document introduces the structure of a paper and provides a miscellany of common mistakes to avoid.

Notes on Writing Mathematics (PDF)

LaTeX Resources

The following PDF, TeX, and Beamer samples guide students to present their work using LaTeX, a high-quality typesetting system designed for the production of technical and scientific documentation. The content in the PDF and TeX documents highlights the structure of a generic student paper.

Sample PDF Document created by pdfLaTeX (PDF)

Sample TeX Document (TEX)

Beamer template (TEX)

The following resources are provided to help students learn and use LaTeX.

LaTeX-Project. “ Obtaining LaTeX .” August 28, 2009.

Downes, Michael. “Short Math Guide for LaTeX.” (PDF) American Mathematical Society . Version 1.09. March 22, 2002.

Oetiker, Tobias, Hubert Partl, et al. “The Not So Short Introduction to LaTeX 2ε.” (PDF) Version 5.01. April 06, 2011.

Reckdahl, Keith. “Using Imported Graphics in LaTeX and pdfLaTeX.” (PDF) Version 3.0.1. January 12, 2006.

Writing Workshop

Each semester there is a writing workshop, led by the lead instructor, which features examples to stimulate discussion about how to write well. In Spring 2013, Haynes ran this workshop during the third class session and used the following slide deck, which was developed by Prof. Paul Seidel and modified with the help of Prof. Tom Mrowka and Prof. Richard Stanley.

The 18.821 Project Report (PDF)

This workshop was held before students had begun to think about the writing component of the course, and it seemed as if the students had to be reminded of the lessons of the workshop when they actually wrote their papers. In future semesters, we plan to offer the writing workshop closer to the time that students are drafting their first paper. We may also focus the examples used in the workshop on the few most important points rather than a broad coverage.

• Download video

This video features the writing workshop from Spring 2013 and includes instruction from Haynes as well as excerpts of the class discussion.

You are leaving MIT OpenCourseWare

• Exploring Computer-Based Math Practice Programs
• Choosing the Right Tutoring Program
• Understanding Complex Mathematics
• Online Math Tutoring: What You Need to Know
• Tutoring Benefits
• Learning Math Fundamentals
• Improving Grades
• Test Prep and Exam Tips
• Tutoring Types
• Online Math Tutoring
• In-Person Math Tutoring
• Group Math Tutoring
• Tutoring Basics
• Finding a Tutor
• Choosing a Tutoring Program
• Tutoring Strategies
• Help Benefits
• Time-Saving Solutions
• Understanding Difficult Concepts
• Expert Advice and Guidance
• Interactive Math Help Tools
• Video Tutorials and Lectures
• Questions and Answers Sites
• Help Basics
• Math Problem Solvers
• Finding Math Help Online
• Homework Help Websites
• Problem Basics
• Working with Word Problems

Choosing the Right Problem-Solving Approach

• Solving Math Problems Step-by-Step
• Problem Benefits
• Improving Problem-Solving Skills
• Becoming More Comfortable with Math
• Gaining Confidence in Math Abilities
• Problem Types
• Calculus Problems
• Geometry Problems
• Algebra Problems
• Practice Basics
• Developing Good Math Habits
• Using Effective Practice Tools
• Creating a Practice Schedule
• Practice Benefits
• Improving Understanding of Math Concepts
• Increasing Speed and Accuracy in Math Skills
• Tracking Progress and Setting Goals
• Practice Types
• Game-Based Math Practice Activities
• Computer-Based Math Practice Programs
• Math Worksheets and Workspace Exercises
• Topic Basics
• Understanding Core Math Subjects
• Researching Relevant Resources
• Exploring Advanced Math Topics
• Topic Types
• Algebra Topics and Concepts
• Calculus Topics and Concepts
• Geometry Topics and Concepts
• Topic Benefits
• Deepening Knowledge of Math Fundamentals
• Gaining Insight into Math Applications
• Developing New Problem-Solving Techniques
• Lesson Basics
• Adapting Lessons to Different Learners
• Identifying Learning Objectives and Goals
• Choosing Appropriate Learning Materials and Resources
• Lesson Types
• Math Lessons for High Schoolers
• Math Lessons for Middle Schoolers
• Math Lessons for Elementary Schoolers
• Lesson Benefits
• Increasing Engagement in Learning Activities
• Improving Retention of Learned Skills and Information
• Developing Understanding of Complex Concepts
• Theory Types
• Calculus Theory and Integration
• Geometric Theory and Shapes

Algebraic Theory and Equations

• Theory Basics
• Analyzing Mathematical Principles
• Understanding Mathematical Notation
• Exploring the History of Mathematics
• Theory Benefits
• Gaining Insight into Mathematical Constructs
• Developing New Problem-Solving Strategies
• Appreciating the Beauty of Mathematics
• Study Benefits
• Formulating New Hypotheses About Mathematics Education
• Developing Expertise in Mathematics Education
• Applying Foundational Knowledge to Real-World Contexts
• Study Types
• Case Studies in Mathematics Education
• Survey Studies in Mathematics Education
• Experimental Studies in Mathematics Education
• Study Basics
• Analyzing Results and Drawing Conclusions
• Identifying Research Questions
• Gathering Relevant Data and Information
• Textbook Benefits
• Establishing Foundational Knowledge
• Gaining Insight into Complex Mathematics
• Developing Ability to Solve Problems Independently
• Textbook Types
• Geometry Textbooks
• Algebra Textbooks
• Calculus Textbooks
• Textbook Basics
• Identifying Appropriate Textbooks
• Choosing Textbooks for Different Grade Levels
• Analyzing Textbook Content for Accuracy
• Prep Benefits
• Gaining Expertise in Different Areas of Mathematics
• Increasing Confidence in Math Abilities
• Improving Performance on Tests and Exams
• Prep Basics
• Using Test Prep Tools Effectively
• Choosing the Right Study Materials
• Creating a Study Plan
• Geometry Exam Prep
• Algebra Exam Prep
• Calculus Exam Prep
• Math Studies

Analyzing Data:

Forming a conclusion:, strategies for analyzing results.

In order to draw meaningful conclusions, it is important to have a strategy for analyzing the data. There are a few different strategies that can be used to analyze results, such as organizing the data into categories, looking for patterns or trends in the data, or using mathematical equations or formulas to determine relationships between different pieces of data. Organizing data into categories is a helpful way to analyze results. This method involves taking the data and grouping it into categories that are related to each other. For example, if you were analyzing test scores, you could group them into categories such as “A” grades, “B” grades, and “C” grades.

This type of analysis allows you to quickly identify patterns or trends in the data. Looking for patterns or trends in the data is another strategy for analyzing results. This involves examining the data to identify any repeating patterns or trends. For example, if you were analyzing test scores, you might look for any trends in how students performed on each section of the test. This type of analysis can help you identify areas where students are struggling and areas where they are excelling. Using mathematical equations or formulas is another way to analyze results.

This method involves using mathematical equations or formulas to determine relationships between different pieces of data. For example, if you were analyzing test scores, you could use an equation to calculate the average score of all students who took the test. This type of analysis can help identify relationships between different pieces of data and can help you draw meaningful conclusions. In summary, analyzing results and drawing conclusions are important skills for students of all ages. Understanding the process of collecting data, analyzing it, and forming conclusions based on evidence can help students develop their critical thinking skills.

By following the strategies outlined above, students can ensure they are completing each stage of the process successfully.

Shahid Lakha

Shahid Lakha is a seasoned educational consultant with a rich history in the independent education sector and EdTech. With a solid background in Physics, Shahid has cultivated a career that spans tutoring, consulting, and entrepreneurship. As an Educational Consultant at Spires Online Tutoring since October 2016, he has been instrumental in fostering educational excellence in the online tutoring space. Shahid is also the founder and director of Specialist Science Tutors, a tutoring agency based in West London, where he has successfully managed various facets of the business, including marketing, web design, and client relationships. His dedication to education is further evidenced by his role as a self-employed tutor, where he has been teaching Maths, Physics, and Engineering to students up to university level since September 2011. Shahid holds a Master of Science in Photon Science from the University of Manchester and a Bachelor of Science in Physics from the University of Bath.

• Case Studies in Mathematics Education: An Overview

Explore case studies in mathematics education to learn more about how different teaching strategies can impact student learning and success.

This article provides guidance on how to identify and formulate research questions that are relevant to Math Studies. It covers the importance of clear and concise research questions, the process of formulating them, and tips for success.

• Calculus Problems: An Overview

Learn all about calculus problems and how to solve them. Find helpful examples and explanations to help you understand the concepts.

This article covers the benefits of gaining insight into math applications, including how to use math to solve everyday problems and how to develop a better understanding of math concepts.

Leave Message

Your email address will not be published. Required fields are marked *

I agree with the terms of service

• Boost Your Math Exam Prep With Increased Confidence in Math Abilities

• Questions and Answers Sites: An Overview
• Video Tutorials and Lectures: Understanding the Benefits and Uses
• Algebra Exam Prep: A Comprehensive Overview
• Exploring Homework Help Websites
• Geometry Problems: A Comprehensive Overview
• Gathering Relevant Data and Information for Math Studies and Study Basics

Analyzing Mathematical Principles: A Comprehensive Overview

• Tips for Improving Performance on Tests and Exams
• Math Problem Solvers: Exploring Solutions and Strategies
• Calculus Exam Prep: A Comprehensive Overview
• Exploring Geometry Textbooks
• Test Prep and Exam Tips: A Comprehensive Guide to Achieve Success
• Experimental Studies in Mathematics Education: An Overview
• Researching Relevant Resources: A Comprehensive Overview
• Creating a Practical Practice Schedule
• Establishing Foundational Knowledge: A Comprehensive Overview
• Creating a Study Plan for Math Exam Prep
• Improve Grades: A Comprehensive Guide
• Understanding Complex Concepts
• In-Person Math Tutoring: Everything You Need to Know
• Tutoring Strategies: A Comprehensive Overview
• Working with Word Problems: An Introduction
• Choosing the Right Study Materials for Math Exam Prep
• Math Lessons for High Schoolers: An Engaging and Informative Guide
• Algebra Textbooks: An Overview
• Explore Geometry Topics and Concepts
• Preparing for Your Geometry Exam
• Exploring the Benefits of Applying Foundational Knowledge to Real-World Contexts
• Group Math Tutoring Explained: Everything You Need to Know
• Unlock the Benefits of Developing Expertise in Mathematics Education
• Calculus Textbooks: Exploring Types, Benefits and More
• Finding Math Help Online: A Comprehensive Overview
• Finding a Tutor: Everything You Need to Know
• Algebra Problems Explained
• How to Teach Math Lessons to Middle Schoolers
• Interactive Math Help Tools: An Informative Overview
• Creating Effective Problem-Solving Strategies
• Unlocking the Math Lessons for Elementary Schoolers

Which cookies do you want to accept?

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Conclusion | Definition & Meaning

JUMP TO TOPIC

Hypothesis and Conclusion

If-then statement, a implies b, conclusion|definition & meaning.

 The term conclusion in maths is used to define us about the problem that we solve and when we produce the final result at the end then that stage of processes is called as conclusion.

Figure 1 – Give the Right Conclusion to the problem 

When you solve a maths question, you have to end the problem by calculating the last answer and pulling a conclus ion by writing the answer.  A conclusion is the last step of the maths problem. The conclusion is the final answer produced in the end . The answer is completed by writing the arguments and statements by telling the answer to the question. The ending statement of a problem is called a conclusion.

Drawing conclusions refers to the act of thinking of interpreting a series of premises or some ideas and, from them, suggesting something that leads to a meaningful finding. It is normally regarded as a conscious way of learning .

As a rule, a mathematical statement comprises two sections : the first section is assumptions or hypotheses , and the other section is the conclusion . Most mathematical statements have the form “If A, then B.” Often, this statement is written as “A implies B” or “A $\Rightarrow $ B.”  The assumptions we make are what makes “A,” and the circumstances that make “B” are called the conclusion .

To prove that a given statement “If A, then B” is said to be true, we will require some assumptions for “A,” and after doing some work on it, we need to conclude that “B” must also hold when “A” holds.

If we are asked to apply the statement “If A, then B,” firstly, we should be sure that the conditions of the statement “A” are met and true before we start to talk about the conclusion “B.”

Suppose you want to apply the statement “x is even $\Rightarrow$ x2 is an integer.” First, you must verify  that x is even  before  you  conclude that x2 is an integer.

In maths, you will, at many times, confront statements in the form “X $\Leftrightarrow$ Y” or “X if and only if Y.”  These statements are actually two “if, then” statements. The following statement, “X if and only if Y,” is logically equivalent to the statements “If X, then Y” and “If Y, then X.” One more method for thinking about this kind of explanation is an equality between the statements X and Y: so, whenever X holds, Y holds, and whenever Y hold, X holds.

Assume the example: “ x is even $\Leftrightarrow$ x 2  is an integer “. Statement A says, “ x is even,” whereas statement B says, “ x 2  is an integer.” If we get a quick revision about what it suggests to be even (simply that x is a multiple of 2), we can see with ease that the following two statements are identical : If x = 2 k is proved to be even, then it implies x 2 = 2 k 2 = k is an integer, and we know that x 2 = k is an integer, then x = 2 k so n is proved to be even.

In day-to-day use, a statement which is in the form “ If A, then B ,” in some cases, means “ A if and only if B. ” For example, when people agree on a deal, they say, “If you agree to sell me your car for 500k, then I’ll buy from you this week” they straightaway mean, “I’ll buy your car if and only if you agree to sell me in 500k.” In other words, if you don’t agree on 500k, they will not be buying your car from you .

In geometry, the validation or proof is stated in the if-then format. The “if” is a condition or hypothesis , and if that condition is met, only then the second part of the statement is true , which is called the conclusion . The working is like any other if-then statement. For illustration, the statement “If a toy shop has toys for two age groups and 45 percent of toys in the shop are for 14 or above years old, then 55 percent of the toys in the shop are for 13 and fewer years old.” The above statement concludes that “55 percent of the toys in the shop are for 13 and fewer years old.”

In maths, the statement “A if and only if B” is very different from “A implies B.” Assume the example: “ x is an integer” is the A statement, and “ x 3 is a rational number” is the B statement  The statement “A implies B” here means “If x is an integer, then x 3 is a rational number.” The statement is proven to be true. On the other hand, the statement, “A, if and only if B,” means “ x is an integer if and only if x 3 is a rational number,” which is not true in this case.

Examples of Drawing Conclusions

Consider the equation below. Comment if this equation is true or false.

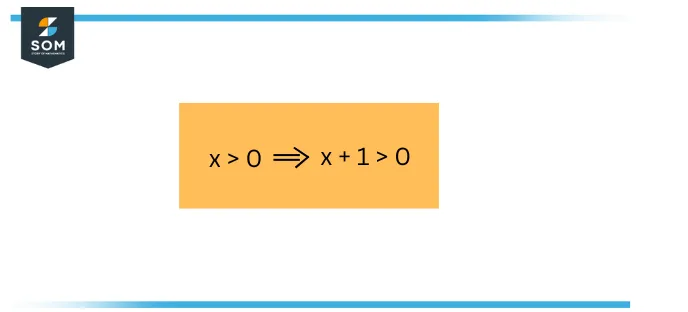
Figure 3 – Example Problem

To calculate its true answer, first, consider the hypothesis $x>0$. Whatever we are going to conclude, it will be a consequence of the truth that $x$ is positive.

Next, consider the conclusion $x+1>0$. This equation is right, since $x+1>x>0$.

This implies that the provided inequality is true.

Simplify the below problem by providing a conclusion by calculating the answer of A.

\[ A= \dfrac{35}{3} \]

The expression given in the question is: $A= \dfrac{35}{3}$

Calculating the answer of A to make a conclusion, The arithmetic operation division is found in the question that is to be figured out in the provided problem. After figuring out the answer to expression A, The conclusion will be given.

\[ A= 11. 667 \]

Therefore, we conclude the question by calculating the answer of $A=11.666$

Consider the equation $0>1 \Rightarrow sinx=2$. Is this equation true or false?

To calculate the correct answer, first consider the hypothesis $0>1$. This equation is clearly false.

calculate the below problem by providing a conclusion by estimating the value of X.

\[ 3+8 \times 2\]

The expression given in the problem is $3+8 \times 2 $.

Multiplication and Plus operation is to be carried out to calculate the answer to the given problem. After figuring out the answer to X  the conclusion will be given.

Thus, we conclude the example by calculating the value of $X = 19$.

All images/mathematical drawings were created with GeoGebra.

Concentric Circles Definition < Glossary Index > Cone Definiton

• The Open University
• Guest user / Sign out
• Study with The Open University

My OpenLearn Profile

Personalise your OpenLearn profile, save your favourite content and get recognition for your learning

About this free course

Become an ou student, download this course, share this free course.

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

We have now looked at a number of different graphs and charts, all of which were potentially misleading. We hope that from now on if you have to work with a graph or a chart, you will always consider the following points:

look carefully at any horizontal or vertical scale that is given;

consider each graph or chart separately, don't compare them unless you are sure that they have the same scales;

if it is not easy to interpret the graph or chart, trying reading off some values.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Definition to Remember:

• Thesis + Wisdom + Catchy Last Line = Conclusion

Rules to Remember:

• Much as your introduction gives readers a first impression of who you are and what you hope to accomplish, your conclusion is your chance to offer final wisdom. For many readers, your concluding words are what they will remember long after they have finished reading your piece. For that reason, your concluding paragraph is critical.
• Always end your essay in a way that reinforces your thesis and your purpose. A conclusion must provide a sense of closure. Readers should recognize your final paragraph as an ending. If you feel compelled to type the words “The End,” you’re not there yet.
• Remember to look ahead. Is there future research that you intend or would recommend? Is there something specific you hope your readers will do with the ideas you have shared? Is there a new direction to turn? How can you use your conclusion to keep your readers thinking, even after they have set your essay aside?
• Remind your readers of your overall thesis . Do not merely repeat your thesis. If you have added sufficient evidence in your essay to support your claim, your thesis should sound different to your readers than it did in the introduction. As you remind your readers of your purpose, allow your thesis to express the fullness of all of the evidence you have brought to bear.
• a related story
• a provocative question or series of questions
• a hypothetical scenario
• a surprising fact or series of facts
• an engaging direct quotation
• a striking statement
• background information or context
• an opposing argument
• the who, what, where, when, and why of the paper’s focus
• a combination of the types listed above
• Finish with a catchy last line that is both conclusive-sounding and memorable. Much like a catchy first line, an effective last line should be concise, poetic, persuasive, and provocative. “Writing well may offer little respect, but writing poorly certainly loses it.” David Hartmann, Director of Client Success

Common Errors:

• Tacking on a placeholder conclusion. Writers are often fatigued by the time they are ready to write that final paragraph, and, unfortunately, it shows. As with any kind of writing, if you are finding the work tedious, imagine how uninterested your readers will be. Always save time to set your work aside and refresh before writing your conclusion; the added effort will always pay off.
• Repeating what has been said already. While many of us were taught in elementary school to use the conclusion as an opportunity to remind your readers of everything you just said, an effective post-elementary school conclusion should aspire for more than merely repetition.

Exercise 13.1

Consider a writing assignment you will need to undertake in the near future. How might you approach a conclusion using each of the following approaches? Be specific as you answer.

• A related story:
• A provocative question or series of questions:
• A hypothetical scenario:
• A surprising fact or series of facts:
• An engaging direct quotation:
• A striking statement:
• Background information or context:
• An opposing argument:
• The who, what, where, when, and why of the paper’s focus:
• A combination of the types listed above:

Exercise 13.2

Consider at least five paragraphs you have written in the past week, whether for work, school, or personal use. Write the last line of each on the lines below. If you had been a member of your own audience, would you have found the last line conclusive but memorable? Why or why not? If not, what revisions would you make?

Exercise 13.3

Select one of the examples from Exercise 13.1 and write a conclusion. Once you have finished, ask yourself the following questions:

• Which of the suggestions listed in Exercise 13.1 have you used to interest and inspire your readers? Why?
• Have you included a repetition of your thesis statement that is a fuller, more complete version of the statement you included in your introduction?
• Have you included a catchy last line?
• If you were a member of your own audience, would you find the conclusion memorable? Why or why not?
• What further revisions do you need to make?

The Simple Math of Writing Well Copyright © 2017 by Dr. Jennie A. Harrop is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Psychological Research

Drawing conclusions from statistics, learning objectives.

• Describe the role of random sampling and random assignment in drawing cause-and-effect conclusions

Generalizability

Figure 1 . Generalizability is an important research consideration: The results of studies with widely representative samples are more likely to generalize to the population. [Image: Barnacles Budget Accommodation]

One limitation to the study mentioned previously about the babies choosing the “helper” toy is that the conclusion only applies to the 16 infants in the study. We don’t know much about how those 16 infants were selected. Suppose we want to select a subset of individuals (a sample ) from a much larger group of individuals (the population ) in such a way that conclusions from the sample can be generalized to the larger population. This is the question faced by pollsters every day.

Example 1 : The General Social Survey (GSS) is a survey on societal trends conducted every other year in the United States. Based on a sample of about 2,000 adult Americans, researchers make claims about what percentage of the U.S. population consider themselves to be “liberal,” what percentage consider themselves “happy,” what percentage feel “rushed” in their daily lives, and many other issues. The key to making these claims about the larger population of all American adults lies in how the sample is selected. The goal is to select a sample that is representative of the population, and a common way to achieve this goal is to select a random sample that gives every member of the population an equal chance of being selected for the sample. In its simplest form, random sampling involves numbering every member of the population and then using a computer to randomly select the subset to be surveyed. Most polls don’t operate exactly like this, but they do use probability-based sampling methods to select individuals from nationally representative panels.

In 2004, the GSS reported that 817 of 977 respondents (or 83.6%) indicated that they always or sometimes feel rushed. This is a clear majority, but we again need to consider variation due to random sampling . Fortunately, we can use the same probability model we did in the previous example to investigate the probable size of this error. (Note, we can use the coin-tossing model when the actual population size is much, much larger than the sample size, as then we can still consider the probability to be the same for every individual in the sample.) This probability model predicts that the sample result will be within 3 percentage points of the population value (roughly 1 over the square root of the sample size, the margin of error ). A statistician would conclude, with 95% confidence, that between 80.6% and 86.6% of all adult Americans in 2004 would have responded that they sometimes or always feel rushed.

The key to the margin of error is that when we use a probability sampling method, we can make claims about how often (in the long run, with repeated random sampling) the sample result would fall within a certain distance from the unknown population value by chance (meaning by random sampling variation) alone. Conversely, non-random samples are often suspect to bias, meaning the sampling method systematically over-represents some segments of the population and under-represents others. We also still need to consider other sources of bias, such as individuals not responding honestly. These sources of error are not measured by the margin of error.

Cause and Effect

In many research studies, the primary question of interest concerns differences between groups. Then the question becomes how were the groups formed (e.g., selecting people who already drink coffee vs. those who don’t). In some studies, the researchers actively form the groups themselves. But then we have a similar question—could any differences we observe in the groups be an artifact of that group-formation process? Or maybe the difference we observe in the groups is so large that we can discount a “fluke” in the group-formation process as a reasonable explanation for what we find?

Example 2 : A psychology study investigated whether people tend to display more creativity when they are thinking about intrinsic (internal) or extrinsic (external) motivations (Ramsey & Schafer, 2002, based on a study by Amabile, 1985). The subjects were 47 people with extensive experience with creative writing. Subjects began by answering survey questions about either intrinsic motivations for writing (such as the pleasure of self-expression) or extrinsic motivations (such as public recognition). Then all subjects were instructed to write a haiku, and those poems were evaluated for creativity by a panel of judges. The researchers conjectured beforehand that subjects who were thinking about intrinsic motivations would display more creativity than subjects who were thinking about extrinsic motivations. The creativity scores from the 47 subjects in this study are displayed in Figure 2, where higher scores indicate more creativity.

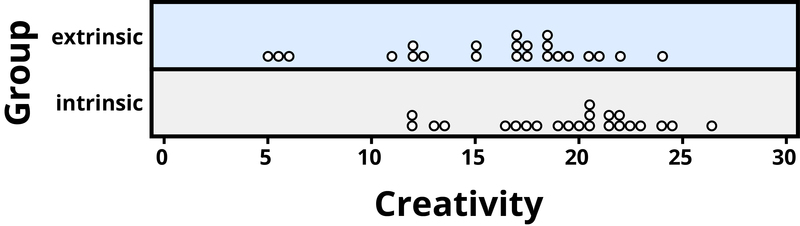
Figure 2 . Creativity scores separated by type of motivation.

In this example, the key question is whether the type of motivation affects creativity scores. In particular, do subjects who were asked about intrinsic motivations tend to have higher creativity scores than subjects who were asked about extrinsic motivations?

Figure 2 reveals that both motivation groups saw considerable variability in creativity scores, and these scores have considerable overlap between the groups. In other words, it’s certainly not always the case that those with extrinsic motivations have higher creativity than those with intrinsic motivations, but there may still be a statistical tendency in this direction. (Psychologist Keith Stanovich (2013) refers to people’s difficulties with thinking about such probabilistic tendencies as “the Achilles heel of human cognition.”)

The mean creativity score is 19.88 for the intrinsic group, compared to 15.74 for the extrinsic group, which supports the researchers’ conjecture. Yet comparing only the means of the two groups fails to consider the variability of creativity scores in the groups. We can measure variability with statistics using, for instance, the standard deviation: 5.25 for the extrinsic group and 4.40 for the intrinsic group. The standard deviations tell us that most of the creativity scores are within about 5 points of the mean score in each group. We see that the mean score for the intrinsic group lies within one standard deviation of the mean score for extrinsic group. So, although there is a tendency for the creativity scores to be higher in the intrinsic group, on average, the difference is not extremely large.

We again want to consider possible explanations for this difference. The study only involved individuals with extensive creative writing experience. Although this limits the population to which we can generalize, it does not explain why the mean creativity score was a bit larger for the intrinsic group than for the extrinsic group. Maybe women tend to receive higher creativity scores? Here is where we need to focus on how the individuals were assigned to the motivation groups. If only women were in the intrinsic motivation group and only men in the extrinsic group, then this would present a problem because we wouldn’t know if the intrinsic group did better because of the different type of motivation or because they were women. However, the researchers guarded against such a problem by randomly assigning the individuals to the motivation groups. Like flipping a coin, each individual was just as likely to be assigned to either type of motivation. Why is this helpful? Because this random assignment tends to balance out all the variables related to creativity we can think of, and even those we don’t think of in advance, between the two groups. So we should have a similar male/female split between the two groups; we should have a similar age distribution between the two groups; we should have a similar distribution of educational background between the two groups; and so on. Random assignment should produce groups that are as similar as possible except for the type of motivation, which presumably eliminates all those other variables as possible explanations for the observed tendency for higher scores in the intrinsic group.

But does this always work? No, so by “luck of the draw” the groups may be a little different prior to answering the motivation survey. So then the question is, is it possible that an unlucky random assignment is responsible for the observed difference in creativity scores between the groups? In other words, suppose each individual’s poem was going to get the same creativity score no matter which group they were assigned to, that the type of motivation in no way impacted their score. Then how often would the random-assignment process alone lead to a difference in mean creativity scores as large (or larger) than 19.88 – 15.74 = 4.14 points?

We again want to apply to a probability model to approximate a p-value , but this time the model will be a bit different. Think of writing everyone’s creativity scores on an index card, shuffling up the index cards, and then dealing out 23 to the extrinsic motivation group and 24 to the intrinsic motivation group, and finding the difference in the group means. We (better yet, the computer) can repeat this process over and over to see how often, when the scores don’t change, random assignment leads to a difference in means at least as large as 4.41. Figure 3 shows the results from 1,000 such hypothetical random assignments for these scores.

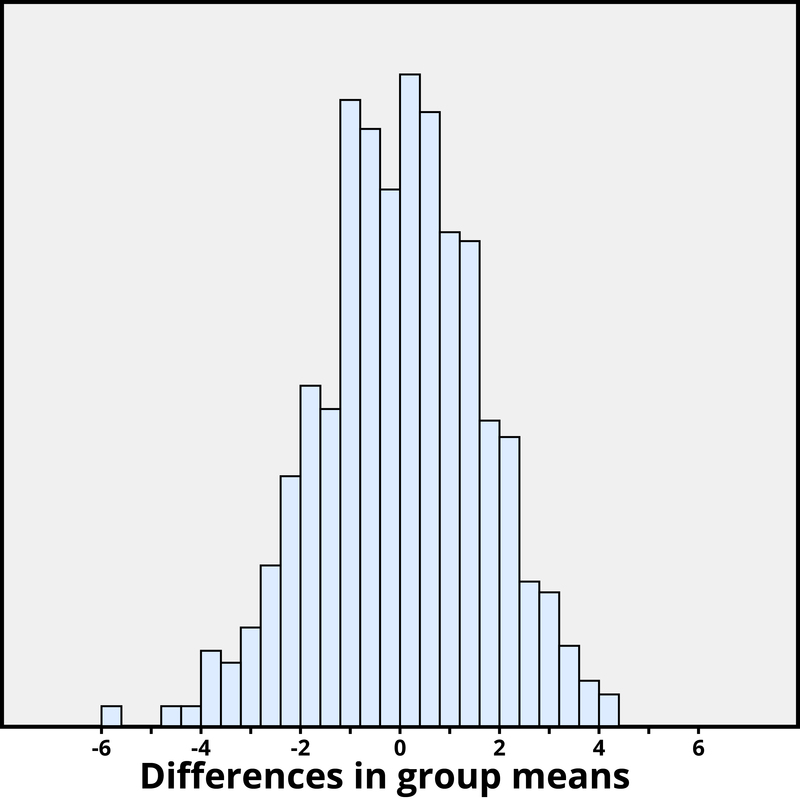
Figure 3 . Differences in group means under random assignment alone.

Only 2 of the 1,000 simulated random assignments produced a difference in group means of 4.41 or larger. In other words, the approximate p-value is 2/1000 = 0.002. This small p-value indicates that it would be very surprising for the random assignment process alone to produce such a large difference in group means. Therefore, as with Example 2, we have strong evidence that focusing on intrinsic motivations tends to increase creativity scores, as compared to thinking about extrinsic motivations.

Notice that the previous statement implies a cause-and-effect relationship between motivation and creativity score; is such a strong conclusion justified? Yes, because of the random assignment used in the study. That should have balanced out any other variables between the two groups, so now that the small p-value convinces us that the higher mean in the intrinsic group wasn’t just a coincidence, the only reasonable explanation left is the difference in the type of motivation. Can we generalize this conclusion to everyone? Not necessarily—we could cautiously generalize this conclusion to individuals with extensive experience in creative writing similar the individuals in this study, but we would still want to know more about how these individuals were selected to participate.

Figure 4 . Researchers employ the scientific method that involves a great deal of statistical thinking: generate a hypothesis –> design a study to test that hypothesis –> conduct the study –> analyze the data –> report the results. [Image: widdowquinn]

Statistical thinking involves the careful design of a study to collect meaningful data to answer a focused research question, detailed analysis of patterns in the data, and drawing conclusions that go beyond the observed data. Random sampling is paramount to generalizing results from our sample to a larger population, and random assignment is key to drawing cause-and-effect conclusions. With both kinds of randomness, probability models help us assess how much random variation we can expect in our results, in order to determine whether our results could happen by chance alone and to estimate a margin of error.

So where does this leave us with regard to the coffee study mentioned previously (the Freedman, Park, Abnet, Hollenbeck, & Sinha, 2012 found that men who drank at least six cups of coffee a day had a 10% lower chance of dying (women 15% lower) than those who drank none)? We can answer many of the questions:

• This was a 14-year study conducted by researchers at the National Cancer Institute.
• The results were published in the June issue of the New England Journal of Medicine , a respected, peer-reviewed journal.
• The study reviewed coffee habits of more than 402,000 people ages 50 to 71 from six states and two metropolitan areas. Those with cancer, heart disease, and stroke were excluded at the start of the study. Coffee consumption was assessed once at the start of the study.
• About 52,000 people died during the course of the study.
• People who drank between two and five cups of coffee daily showed a lower risk as well, but the amount of reduction increased for those drinking six or more cups.
• The sample sizes were fairly large and so the p-values are quite small, even though percent reduction in risk was not extremely large (dropping from a 12% chance to about 10%–11%).
• Whether coffee was caffeinated or decaffeinated did not appear to affect the results.
• This was an observational study, so no cause-and-effect conclusions can be drawn between coffee drinking and increased longevity, contrary to the impression conveyed by many news headlines about this study. In particular, it’s possible that those with chronic diseases don’t tend to drink coffee.

This study needs to be reviewed in the larger context of similar studies and consistency of results across studies, with the constant caution that this was not a randomized experiment. Whereas a statistical analysis can still “adjust” for other potential confounding variables, we are not yet convinced that researchers have identified them all or completely isolated why this decrease in death risk is evident. Researchers can now take the findings of this study and develop more focused studies that address new questions.

Explore these outside resources to learn more about applied statistics:

• Video about p-values:  P-Value Extravaganza
• Interactive web applets for teaching and learning statistics
• Inter-university Consortium for Political and Social Research  where you can find and analyze data.
• The Consortium for the Advancement of Undergraduate Statistics

Think It Over

• Find a recent research article in your field and answer the following: What was the primary research question? How were individuals selected to participate in the study? Were summary results provided? How strong is the evidence presented in favor or against the research question? Was random assignment used? Summarize the main conclusions from the study, addressing the issues of statistical significance, statistical confidence, generalizability, and cause and effect. Do you agree with the conclusions drawn from this study, based on the study design and the results presented?
• Is it reasonable to use a random sample of 1,000 individuals to draw conclusions about all U.S. adults? Explain why or why not.

cause-and-effect: related to whether we say one variable is causing changes in the other variable, versus other variables that may be related to these two variables. generalizability : related to whether the results from the sample can be generalized to a larger population. margin of error : the expected amount of random variation in a statistic; often defined for 95% confidence level. population : a larger collection of individuals that we would like to generalize our results to. p-value : the probability of observing a particular outcome in a sample, or more extreme, under a conjecture about the larger population or process. random assignment : using a probability-based method to divide a sample into treatment groups. random sampling : using a probability-based method to select a subset of individuals for the sample from the population. sample : the collection of individuals on which we collect data.

Contribute!

Improve this page Learn More

• Modification, adaptation, and original content. Authored by : Pat Carroll and Lumen Learning. Provided by : Lumen Learning. License : CC BY: Attribution
• Statistical Thinking. Authored by : Beth Chance and Allan Rossman, California Polytechnic State University, San Luis Obispo. Provided by : Noba. Located at : http://nobaproject.com/modules/statistical-thinking . License : CC BY-NC-SA: Attribution-NonCommercial-ShareAlike
• The Replication Crisis. Authored by : Colin Thomas William. Provided by : Ivy Tech Community College. License : CC BY: Attribution

Network Science (2005)

Chapter: 8 conclusions and recommendations, 8 conclusions and recommendations.

In this chapter the committee combines its findings into conclusions and offers recommendations. First, it collects the factual findings presented in Chapters 2 - 7 into three overarching conclusions concerning the importance of networks and the current state of knowledge about them. Next, it articulates specific conclusions that are directly responsive to Items 1 through 3 of the statement of task. Finally, in response to Item 4, the committee provides its recommendations, including for research initiatives. Box 8-1 summarizes how the report responds to the statement of task.

OVERARCHING CONCLUSIONS

Conclusion 1. Networks are pervasive in all aspects of life: biological, physical, and social. They are indispensable to the workings of a global economy and to the defense of the United States against both conventional military threats and the threat of terrorism.

Conclusion 1 was developed in Chapters 2 and 3 and summarized in Tables 2-1 , 2-2 , and 3-1 and the discussions surrounding them. It sets the stage for the committee’s inquiry into the state of knowledge about these networks.

Conclusion 2. Fundamental knowledge about the prediction of the properties of complex networks is primitive.

Given the pervasiveness and vital importance of networks, one might assume that a lot is known about them. As documented in Chapters 5 and 6 , however, this is not the case. Although the technology for constructing and operating engineered physical networks is sophisticated, critical questions about their robustness, stability, scaling, and performance cannot be answered with confidence without extensive simulation and testing. For large global networks, even simulations are often inadequate. The design and operation of network components (such things as computers, routers, or radios) are based on fundamental knowledge gleaned from physics, chemistry, and materials science. However, there is no comparable fundamental knowledge that allows the a priori prediction of the properties of complex assemblies of these components into networks. Indeed, such networks are expected to exhibit emergent behaviors—that is, behaviors that cannot be predicted or anticipated from the known behaviors of their components. In the case of social and biological networks, even the properties of the components are poorly known. A huge gap exists between the demand for knowledge about the networks on which our lives depend and the availability of that knowledge.

The committee learned that developing predictive models of the behavior of large, complex networks is difficult. There are relatively few rigorous results to describe the scaling of their behaviors with increasing size. Surprisingly, this is true for common engineered networks like the Internet as well as for social and biological networks.

Simulation rather than analysis is the research tool of choice. In the case of social networks, even simulation is vastly complicated by the diversity and complexity of the agents that are the nodes of the networks—humans or groups of humans “in the wild.” Which of their many properties are relevant for developing mathematical models of a particular phenomenon? Existing models of social networks, moreover, represent highly simplified situations and not necessarily ones that are relevant to the Army or network-centric warfare.

Finally, the notion of using network models in biology is relatively new. Controversy swirls around their utility, indeed around that of systems biology itself. In spite of a burgeoning literature on the structure of simple networks, the advancement of the field to allow relating basic scientific results to applications of societal and military interest still lies mostly in the future.

Conclusion 3. Current funding policies and priorities are unlikely to provide adequate fundamental knowledge about large complex networks.

Fundamental knowledge is created and stockpiled in disciplinary environments, mostly at universities, and then used as required by (vertically integrated) industries to provide the products and services required by customers, including the military. This fundamental knowledge is different in kind from empirical knowledge gleaned during the development of technology and products. You get what you measure. Suppliers of fundamental knowledge measure publications, presentations, students supervised, awards received, and other metrics associated with individual investigators. The knowledge accumulates along traditional disciplinary lines because this is where the rewards are found. Large team activities are

relatively rare (except in medicine and large-scale physics experiments) and are mostly left to the consumers of the fundamental knowledge, who must supplement the fundamental knowledge generously with empirical knowledge to convert it into the goods and services desired by the paying customer.

This scheme worked marvelously for more than a half a century, when the United States dominated the world and industries were vertically integrated. With the onset of the global economy in the 1990s, however, the situation began to change dramatically, for a number of reasons. First, knowledge, investment capital, technology, and technical labor are becoming globally available commodities. Second, economic activity, including R&D, is becoming global in scale. Third, these two trends are making the networks on which we depend ever larger and more complex and their susceptibility to disruption ever greater.

This traditional scheme does not work well for generating knowledge about global networks, because focused, coordinated efforts are needed. Thus, there is a huge difference between the social and financial arrangements needed to gain fundamental knowledge about large, complex networks in a global environment and the arrangements that worked so well to provide such knowledge for the design and production of smaller, less complex entities in a national environment. Any successful effort to create the knowledge necessary to secure robust, reliable scalable global networks must come to grips with this reality.

Overall, the committee is led to a view of networks as pervasive in and vital to modern society, yet understood only as well as the solar system was understood in Ptolemy’s time. The military has made networks the centerpiece of its transformation effort without a methodology to design networks in the physical and information domains in a predictive way for network-centric operations (NCO). Further, according to the DOD Office of Force Transformation, research in the cognitive and social domains has yet to yield advances comparable to the technological developments in the information domain. At the same time, current efforts by academia to describe networks are fragmented and disjointed. Relatively little of the current research on networks promises to create a science of networks that will generate knowledge adequate to meet the demand.

In short, there is a massive disconnect between the importance of networks in modern society and military affairs on the one hand and, on the other, the support of coherent R&D activities that would raise current network technologies and capabilities to the next level. The Army alone cannot transform this situation, but it can make a beginning.

SPECIFIC CONCLUSIONS

Items 1 and 2 in the statement of task inquire into the appropriateness of a field of investigation called network science and its definition, content, and the research challenges that would characterize it. Elements of a field of network science have begun to emerge in different disciplines spanning engineering, biological, and social networks. The emerging field is concerned with the development and analysis of network representations to create predictive models of observed physical, biological, and social phenomena.

The remarkable diversity and pervasiveness of network ideas renders the study of network science a highly leveraged topic for both civilian and military investment. The provisional consensus around its core content clearly defines the notion of network science. By making an investment in network science, the Army could forge a single approach to a diverse collection of applications.

Conclusion 4. Network science is an emerging field of investigation whose support will address important societal problems, including the Army’s pursuit of network-centric operations capabilities.

Although the boundaries of network science are fuzzy, there is broad agreement on key topics that should be included within the field, the types of tools that must be developed, and the research challenges that should be investigated. These were documented in Chapters 3 and 4 .

Conclusion 5. There is a consensus among the practitioners of research on networks for physical, biological, social, and information applications on the topics that make up network science.

Responses to its questionnaire greatly assisted the committee in determining “the key research challenges to enable progress in network science.” These responses establish that there is a fair degree of consensus on these challenges across practitioners in diverse applications areas.

Conclusion 6. There are seven major research challenges the surmounting of which will enable progress in network science:

Dynamics, spatial location, and information propagation in networks. Better understanding of the relationship between the architecture of a network and its function is needed.

Modeling and analysis of very large networks. Tools, abstractions, and approximations are needed that allow reasoning about large-scale networks, as well as techniques for modeling networks characterized by noisy and incomplete data.

Design and synthesis of networks. Techniques are needed to design or modify a network to obtain desired properties.

Increasing the level of rigor and mathematical structure. Many of the respondents to the questionnaire felt that the current state of the art in network

science did not have an appropriately rigorous mathematical basis.

Abstracting common concepts across fields. The disparate disciplines need common concepts defined across network science.

Better experiments and measurements of network structure. Current data sets on large-scale networks tend to be sparse, and tools for investigating their structure and function are limited.

Robustness and security of networks. Finally, there is a clear need to better understand and design networked systems that are both robust to variations in the components (including localized failures) and secure against hostile intent.

These challenges are elaborated in terms of specific research issues and their theoretical, experimental, and practical difficulties in Chapter 7 and Appendix E within the framework of exploring various investment scenarios. The scenarios respond to Item 3 in the statement of task.

Although all the military services have a vision of the future in which engineered communications networks play a fundamental role, there is no methodology for ensuring that these networks are scalable, reliable, robust, and secure. Of particular importance is the ability to design networks whose behaviors are predictable in their intended domains of applications. This also is true in the commercial sphere. Creation of such a methodology is an especially pressing task because global commercial networks can also be exploited by criminal and terrorist social networks.

Conclusion 7. The high value attached to the efficient and failure-free operation of global engineered networks makes their design, scaling, and operation a national priority.

RECOMMENDATIONS

The statement of task requests investment recommendations from the committee. Options for these recommendations are explored in Chapter 7 and Appendix E . The committee documents in Chapters 2 and 3 that the impact of networks on society transcends their impact on military applications, although both are vital aspects of the total picture. Chapters 3 and 4 explain that the current state of knowledge about networks does not support the design and operation of complex global networks for current military, political, and economic applications. Advances in network science are essential to developing adequate knowledge for these applications.

Recommendation 1. The federal government should initiate a focused program of research and development to close the gap between currently available knowledge about networks and the knowledge required to characterize and sustain the complex global networks on which the well-being of the United States has come to depend.

This recommendation is buttressed by centuries of evidence that disruptive social networks (e.g., terrorists, criminals) learn to exploit evolving infrastructure networks (e.g., communications or transportation) in ways that the creators of these networks did not anticipate. The global war on terrorism, which is a main driver of military transformation, is only one recent manifestation of this general pattern. Society has the same need in other areas, such as control of criminal activities perpetrated using the global airline and information infrastructures. Addressing problems resulting from the interaction of social and engineered networks is an example of a compelling national issue that transcends the transformation of the military and that is largely untouched by current research on networks.

Within this broad context, Recommendations 1a, 1b, and 1c provide the Army with three options:

Recommendation 1a. The Army, in coordination with other federal agencies, should underwrite a broad network research initiative that includes substantial resources for both military and nonmilitary applications that would address military, economic, criminal, and terrorist threats.

The Army can lead the country in creating a base of network knowledge that can support applications for both the Army and the country at large. Maximum impact could be obtained by a coordinated effort across a variety of federal agencies, including the DOD and the Department of Homeland Security, to create a focused national program of network research that would develop applications to support not only NCO but also countermeasures against international terrorist and criminal threats.

Alternatively, if the Army is restricted to working just with the DOD, it should initiate a focused program to create an achievable vision of NCO capabilities across all the services.

Recommendation 1b. If the Army wants to exploit fully applications in the information domain for military operations in a reasonable time frame and at an affordable cost, it should champion the initiation of a high-priority, focused DOD effort to create a realizable vision of the associated capabilities and to lay out a trajectory for its realization.

Finally, if the Army elects to apply the insight from the committee primarily to its own operations, it can still provide leadership in network science research.

TABLE 8-1 Network Research Areas

Recommendation 1c. The Army should support an aggressive program of both basic and applied research to improve its NCO capabilities.

Specific areas of research of interest to the Army are shown in Table 8-1 . This table expresses the committee’s assessment of the relative priorities for these areas, the time frames in which one might reasonably expect them to be consummated as actionable technology investment options, and the degree of commercial interest in exploiting promising options. Specific research problems and sample projects are given in Appendix E . The committee notes that both trained personnel and promising research problems exist in many of these areas, so the Army should be able to create a productive program readily.

By selecting from among Recommendations 1a through 1c an option that is ambitious yet achievable, the Army can lead the country in creating a base of knowledge emanating from network science that is adequate to support applications on which both the Army and the country at large depend. Regardless of which option (or options) are adopted, Army initiatives in network science should be grounded in basic research.

Recommendation 1d. The initiatives recommended in 1, 1a, 1b, and 1c should include not only theoretical studies but also the experimental testing of new ideas in settings sufficiently realistic to verify or disprove their use for intended applications.

Recommendations 1, 1a, 1b, and 1c span only part of the investment opportunity space—namely, those segments of the space described in Scenarios 2 and 3 in Chapter 7 and Appendix E . They will involve substantial changes in how the Army invests its R&D dollars and in how it plans and manages these investments.

The Army also has the opportunity associated with Scenario 1 in Chapter 7 , which involves funding a small program of basic research in network science. This investment of relatively small amounts of Army risk capital funds would create a base of knowledge and personnel from which the Army could launch an attack on practical problems that arise as it tries to provide NCO capabilities.

Investments in basic (6.1) research in network science can generate significant value; however, the committee wants to be crystal clear that such investments have no immediate prospects of impacting the design, testing, evaluation, or sourcing of NCO capabilities. They would create additional knowledge that builds the core content of network science, and they would train researchers who could also be recruited by the Army for later efforts. While the knowledge generated would probably be less valuable than in the case

of Scenarios 2 and 3, the cost is less and implementation can be immediate.

If the Army elects to exploit Scenario 1, the committee offers the following two further recommendations:

Recommendation 2. The Army should make a modest investment of at least $10 million per year to support a diverse portfolio of basic (6.1) network research that promises high leverage for the dollars invested and is clearly different from existing investments by other federal agencies like the National Science Foundation (NSF), the Department of Energy (DOE), and the National Institutes of Health (NIH).

This modest level of investment is compatible with the Army’s current R&D portfolio. There is an adequate supply of promising research topics and talented researchers to make this investment productive. Additionally, it can be implemented within the Army’s current R&D management work processes, although some enhancements along the lines noted in Chapter 7 and Appendix E would improve the return on this investment.

To identify the topics in basic network science research that would bring the most value to NCO, the committee recalls that the open system architectures for computer networks consist of layers, each of which performs a special function regarded as a “service” by the layers above. It is useful to distinguish among the lower (physical and transport) layers of this architecture, the higher (applications) layers that are built on top of them to offer services to the people, and the cognitive and social networks that are built higher still, on top of the services-to-humans layers.

Research on the lower layers of the network architecture is relatively mature. Improving the services offered at these levels is more of an engineering problem than one requiring basic research. The most immediate payoffs from network science are likely to result from research associated with the upper levels of the network architecture and the social networks that are built at an even higher level upon their outputs. This is where the committee thinks that Army investments are most likely to create the greatest value.

An area of particular promise that has little or no current investment is the social implications of NCO for the organizational structure and command and control. Basic research could provide valuable insight into how military personnel use advanced information exchange capabilities to improve combat effectiveness. For example, one might study how troops in combat could use these capabilities to make better decisions. Additional basic research in the core content of network science might help to determine how the Army can most productively utilize the capabilities of its advanced information infrastructure.

Recommendation 3. The Army should fund a basic research program to explore the interaction between information networks and the social networks that utilize them.

The Army can implement Recommendations 2 and 3 within the confines of its present policies and procedures. They require neither substantial replanning nor the orchestration of joint Army/university/industry research projects. They create significant value and are actionable immediately.

The committee’s Recommendations 1, 1a through 1d, 2, and 3 give the Army an actionable menu of options that span the opportunity space available. By selecting and implementing appropriate items from this menu, the Army can develop a robust network science to “enable progress toward achieving Network-Centric Warfare capabilities,” as requested in the statement of task.

This page intentionally left blank.

The military is currently attempting to develop itself into a force capable of networkcentric operations. While this effort has highlighted the military’s dependence on interacting networks, it has also shown that there is a huge gap between what we need to know about networks and our fundamental knowledge about network behavior. This gap makes the military vision of NCO problematic. To help address this problem, the Army asked the NRC to find out whether identifying and funding a new field of “network science” could help close this gap. This report presents an examination of networks andthe military, an analysis of the promise, content, and challenges of network science, and an assessment of approaches to creating value from network science.

READ FREE ONLINE

Welcome to OpenBook!

You're looking at OpenBook, NAP.edu's online reading room since 1999. Based on feedback from you, our users, we've made some improvements that make it easier than ever to read thousands of publications on our website.

Do you want to take a quick tour of the OpenBook's features?

Show this book's table of contents , where you can jump to any chapter by name.

...or use these buttons to go back to the previous chapter or skip to the next one.

Jump up to the previous page or down to the next one. Also, you can type in a page number and press Enter to go directly to that page in the book.

Switch between the Original Pages , where you can read the report as it appeared in print, and Text Pages for the web version, where you can highlight and search the text.

To search the entire text of this book, type in your search term here and press Enter .

Share a link to this book page on your preferred social network or via email.

View our suggested citation for this chapter.

Ready to take your reading offline? Click here to buy this book in print or download it as a free PDF, if available.

Get Email Updates

Do you enjoy reading reports from the Academies online for free ? Sign up for email notifications and we'll let you know about new publications in your areas of interest when they're released.

13.2 Math and the Environment

Learning objectives.

After completing this section, you should be able to:

• Compute how conserving water can positively impact climate change.
• Discuss the history of solar energy.
• Compute power needs for common devices in a home.
• Explore advantages of solar power as it applies to home use.

Climate change and emissions management have been debated topics in recent years. However, more and more people are recognizing the impacts that have resulted in temperature changes and are seeking timely and effective action. The World Meteorological Organization shared in a June 2021 publication that “2021 is a make-or-break year for climate action, with the window to prevent the worst impacts of climate change—which include ever more frequent more intense droughts, floods and storms—closing rapidly.” The problem no longer belongs to a few countries or regions but rather is a worldwide concern measured with increasing temperatures leading to decreased glacier coverage and resulting rise in sea levels.

The good news is, there are small steps that each of us can do that collectively can positively impact climate change.

Making a Positive Impact on Climate Change—Water Usage

Our use of water is one element that impacts climate change. Having access to clean, potable water is critical for not only our health but also for the health of our ecosystem. About 1 out of 10 people on our planet do not have easy access to clean water to drink. As each of us conserves water, we prolong the life span of fresh water from our lakes and rivers and also reduce the impact on sewer systems and drainage in our communities. Additionally, as we conserve water, we also conserve electricity that is used to bring water to and in our homes. So, what can we do to help conserve water?

Example 13.5

Brushing your teeth (one person’s contribution).

Brushing your teeth with the water running continually uses about 4 gal of water. Turning the faucet off when you are not rinsing uses less than one-fourth of a gallon of water. Considering the recommendation to brush your teeth twice a day, how much water would be saved in a week if the faucet was off when not rinsing?

Leaving the water running continually:

Step 1: Calculate gallons used not with water running continually:

Brushing twice a day for 7 days using 4 gal of water for each brushing

( 2 times a day ) ( 7 days ) ( 4 gal ) = 56 gal ( 2 times a day ) ( 7 days ) ( 4 gal ) = 56 gal

Step 2: Calculate gallons used turning the faucet off when you are not rinsing:

Brushing twice a day for 7 days using 0.25 gal of water for each brushing

( 2 times a day ) ( 7 days ) ( 0.25 gal ) = 3.5 gal ( 2 times a day ) ( 7 days ) ( 0.25 gal ) = 3.5 gal

Step 3: Calculate savings:

Savings = 56 gal − 3.5 gal = 52.5 gal Savings = 56 gal − 3.5 gal = 52.5 gal

During one week, 52.5 gal of water would be saved if one person turned the faucet off except when rinsing when brushing your teeth.

Your Turn 13.5

Example 13.6, brushing your teeth (multiple people’s contribution – town).

Using the data in Example 13.5 , how much water would be saved in a month if one-fifth of a town’s population of 15,000 turned the faucet off when brushing their teeth except when rinsing?

Step 1: From Example 13.5 , we found that 1 person saves 52.5 gal per week.

Step 2: Calculate the population to save water:

One-fifth of 15,000 people = 3,000 people One-fifth of 15,000 people = 3,000 people

Step 3: One-fifth of a town’s population turning off the faucet when brushing their teeth for a month:

( 3,000 ) ( 52.5 gal per week ) ( 4 weeks ) = 630,000 gal ( 3,000 ) ( 52.5 gal per week ) ( 4 weeks ) = 630,000 gal

During one month, 630,000 gallons of water would be saved if one-fifth of a town of 15,000 people turned the faucet off except when rinsing when brushing their teeth.

Your Turn 13.6

Example 13.7, brushing your teeth (multiple people’s contribution – state).

Using the data in Example 13.5 , how much water would be saved in a year if one-fourth of the population of the state of Minnesota, which is approximately 5.6 million people, turned the faucet off when brushing their teeth except when rinsing for a year (52 weeks)?

One-fourth of 5.6 million people = 1.4 million people One-fourth of 5.6 million people = 1.4 million people

Step 3: One-fourth of a town’s population turning off the faucet when brushing their teeth for a month:

( 1.4 million ) ( 52.5 gal per week ) ( 52 weeks ) = 3,822 million gal ( 1.4 million ) ( 52.5 gal per week ) ( 52 weeks ) = 3,822 million gal

During one year, 3,822 million gal of water would be saved if one-fourth of the state of Minnesota turned the faucet off except when rinsing when brushing their teeth.

Your Turn 13.7

History of solar energy.

In the mid-1800s, Willoughby Smith discovered photoconductive responsiveness in selenium. Shortly thereafter, William Grylls Adams and Richard Evans Day discovery that selenium can produce electricity if exposed to the sun was a major breakthrough. Less than 10 years later, Charles Fritts invented the first solar cells using selenium. Jumping a mere 100 years later, Bell Labs in the United States produced the first practical photovoltaic cells in the mid-1950s and developed versions used to power satellites in the same decade.

Solar panel use has exploded in recent decades and is now used by residences, organizations, businesses, and government buildings such as the White House, space to power satellites, and various methods of transportation. One reason for the expansion is a continuing drop in cost combined with an increase in performance and durability. In the mid-1950s, the cost of a solar panel was around $300 per watt capability. Twenty years later, the cost was a third of the 1950s’ cost. Currently, solar panel cost has dropped to less than $1 per watt while decreasing in size as well as increasing in longevity. The dropping price and improved performance has moved solar to a modest investment that can pay for itself in less than half the time of systems from 15 years ago.

Solar Power’s Age

The sun has been harnessed by humans for centuries. The earliest recorded use of tapping the sun’s energy for power dates back to the seventh century BC when man focused the sun’s rays through a magnifying glass to create fire. Four thousand years later, we find historical record of using mirrors to focus the sun and light torches, often for ceremonial proceedings. Use of the sun to light torches continued through the centuries and has been recorded by various cultures including the Chinese civilization in 20 AD and beyond.

In more recent years, the sun was harnessed to power ovens on ships traversing to oceans in the 1700s. At the same time, the power of the sun was utilized to power steamboats through the 1800s. Mária Telkes, a Hungarian-born American scientist, invented a widely deployed solar seawater distiller used on World War II life rafts. Soon after, she partnered with architect Eleanor Raymond to design the first modern home to be completely heated by solar power. Air warmed on rooftop collectors transferred heat to salts, which stored the heat for later use.

Although solar panels as we know them today are relatively new in history, use of the sun to harness power is much older.

Compute Power Needs for Common Home Devices

A kilowatt (kW) is 1,000 watts (W). A kilowatt-hour (kWh) is a measurement of energy use, which is the amount of energy used by a 1,000-watt device to run for an hour. Using the definition of a kilowatt-hour, to calculate how long it would take to consume 1 kWh of power, we divide 1,000 by the watts use of a device.

1,000 / watts = time needed to use 1 kW 1,000 / watts = time needed to use 1 kW

For example, a 75 W bulb would take 1,000 ÷ 75 = 13.3 hours 1,000 ÷ 75 = 13.3 hours to use 1 kW of power.

watts / 1 , 000 = kilowatt hours watts / 1 , 000 = kilowatt hours

Example 13.8

Calculating the kilowatt-hours needed to run a television.

A 48 in plasma television uses about 200 W. How many kilowatt-hours are needed to run the television in a month if the television is one for an average of 2.5 hours a day?

Step 1: 1,000 / ( 200 watts ) = 5 hours 1,000 / ( 200 watts ) = 5 hours to use 1 kW

Step 2: ( 2.5 hours a day ) ( 30 days ) = 75 hours ( 2.5 hours a day ) ( 30 days ) = 75 hours of use

Step 3: 75 hour / 5 hours per kW = 15 kW 75 hour / 5 hours per kW = 15 kW

The television will consume about 15 kW in a month.

Your Turn 13.8

Example 13.9, calculating the cost to run a refrigerator.

A medium-sized Energy Star–rated refrigerator uses about 575 W and runs for about 8 hours per day. What is the monthly (30 days) cost of running the refrigerator if the electric rate is 12 cents per kilowatt-hour?

Step 1: Calculate the watts per day:

( 575 W ) ( 8 hours ) = 4,600 W per day ( 575 W ) ( 8 hours ) = 4,600 W per day

Step 2: Calculate the kilowatt-hours.

( 4,600 ) / ( 1,000 ) = 4.6 kWh ( 4,600 ) / ( 1,000 ) = 4.6 kWh

Step 3: Calculate the daily cost.

( 4.6 kWh ) ( 12 cents ) = 55 cents = $ 0.55 ( 4.6 kWh ) ( 12 cents ) = 55 cents = $ 0.55

Step 4: Calculate the monthly cost.

( $ 0.55 ) ( 30 ) = $ 16.50 ( $ 0.55 ) ( 30 ) = $ 16.50

It would cost about $16.50 to run the refrigerator for a month.

Your Turn 13.9

Example 13.10, calculating the kilowatt-hours to run an oven.

An electric oven is labeled as 4,000 W. How much would it cost to bake a cake for 30 minutes if the electric rate is 14 cents per kilowatt-hour?

Step 1: Determine the time it takes to use 1 kW of power:

1,000 / ( 4,000 watts ) = 0.25 hours to use 1 kW 1,000 / ( 4,000 watts ) = 0.25 hours to use 1 kW

For every 15 minutes, the oven uses 1 kW of power.

Step 2: Determine how many kilowatt-hours are needed to bake the cake for 30 minutes:

( 30 minutes ) / ( 15 minutes per kW ) = 2 kW ( 30 minutes ) / ( 15 minutes per kW ) = 2 kW

Step 3: Calculate the cost of the oven usage:

( 2 kW ) ( 14 cents per kWh ) = 28 cents ( 2 kW ) ( 14 cents per kWh ) = 28 cents

It would cost about 28 cents to bake the cake.

Your Turn 13.10

Solar advantages.

There are multiple advantages that solar power can offer us today including reducing greenhouse gas and CO 2 emissions, powering vehicles, reducing water pollution, reducing strain on limited supply of other power options such as fossil fuels. We will look further at reducing greenhouse gas and CO 2 emissions.

Any gas that prevents infrared radiation from escaping Earth's atmosphere is a greenhouse gas. There are 24 currently identified greenhouse gases of which carbon dioxide is one. When measuring the impact of any of the greenhouse gases, the measurements are given in units of carbon dioxide emissions. For this reason, greenhouse gas and carbon dioxide have become interchangeable in discussions.

People in Mathematics

Charles fritts and mohammad m. atalla.

Charles Fritts, a New York inventor, is credited with creating the first solar cell, which he installed on a rooftop in New York City in 1884. While the solar cell was not very efficient, having a rate of conversion between 1 to 2%, this was a major step early in solar power energy. Today’s solar cells have an efficiency on average of 15 to 20%, which yields a notably higher impact. Nonetheless, the work that Fritts successfully completed marked the start of solar energy through the use of photovoltaic solar panels in the United States.

Mohamed M. Atalla was an Egyptian-born scientist who moved to the United States to complete his studies, and undertook research and development at Bell Laboratories in New Jersey. Many of the early efficiency gains in solar cells were due to his development of processes for using silicon within electronic devices. Atalla's work led to the invention of silicon transistors and microchips (including his own invention of the MOSFET, the most widely used transistor in the world), and quickly increased the efficiency of solar cells.

Example 13.11

Calculating the solar power for average home use in kilowatts.

If a home uses approximately 30 kW of electricity per day, what size solar system would be needed to fuel 80% of a home’s needs for a month (30 days)?

( 30 kW hours ) ( 30 days ) ( 0.80 ) = 720 kW ( 30 kW hours ) ( 30 days ) ( 0.80 ) = 720 kW

A solar system capable of producing 720 kW a month would be needed.

Your Turn 13.11

Check your understanding, section 13.2 exercises.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

• Authors: Donna Kirk
• Publisher/website: OpenStax
• Book title: Contemporary Mathematics
• Publication date: Mar 22, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
• Section URL: https://openstax.org/books/contemporary-mathematics/pages/13-2-math-and-the-environment

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Eur J Investig Health Psychol Educ

Mathematics Classroom Assessment: A Framework for Designing Assessment Tasks and Interpreting Students’ Responses

Classroom assessment could contribute substantially to improving students’ mathematics learning. The process of classroom assessment involves decisions about how to elicit evidence, how to interpret it, and how to use it for teaching and learning. However, the field still needs to further explore how assessment tasks could guide forthcoming instructional adjustments in the mathematics classroom. Towards the endeavor of unpacking the classroom assessment, we present a framework that provides a lens to capture the interplay between the design of mathematics assessment tasks and the analysis of students’ responses. To do so, we relied on existing frameworks of mathematics assessment tasks, and on issues that pertain to the design of tasks. The proposed framework consists of three types of mathematics assessment tasks, their respective competencies, and the characterization of students’ responses. The framework is exemplified with students’ responses from a fourth-grade classroom, and is also used to sketch different students’ profiles. Issues regarding the interpretation of students’ responses and the planning of instructional adjustments are discussed.

1. Introduction

1.1. scope of the paper.

Classroom assessment serves as a process for gathering and interpreting evidence to identify students’ progress in order to make decisions about forthcoming actions in day-to-day teaching [ 1 , 2 ]. It would be particularly useful to have lenses that support the interpretation of the evidence elicited from students’ responses in a systematic manner, in order to better understand where students stand on the learning continuum, and in what ways students’ learning could be enhanced. In this paper, we focus on a planned process—that of written assessment tasks. Mathematics tasks differ based on the expected cognitive demand, the mathematical competencies, the thinking processes, the solution strategies, the level of students’ understanding that determine the ways students respond to the tasks, and the kind of information elicited. However, there are limitations in existing frameworks, due to placing less emphasis on the interplay between mathematics assessment tasks and ways of interpreting the evidence elicited from the tasks that could lead to the decision making regarding forthcoming instructional adjustments. Limitations also result from not attending to the bounded classroom context and the descriptive features of students’ work.

Herein, we present a two-dimensional framework that attempts to align the design of assessment tasks with the ways students’ responses could be analyzed. The design of the tasks is intended to elicit information about students’ competencies in mathematics tasks with various levels of contextual familiarity. We also investigate the ways in which students’ responses could be analyzed. The contribution of this framework lies in the identification of a selected competency for each type of mathematics task, which is then used to characterize students’ work. In this way, the framework attempts to characterize descriptive features of students’ work, which are more likely to provide information for effective feedback [ 3 ]. We also use empirical data from fourth-grade students to sketch students’ profiles, and then turn to discuss how it would be possible to align these profiles with forthcoming instructional adjustments.

1.2. Literature Review

We focus on classroom assessment for formative purposes, using tasks of everyday mathematics to elicit evidence of students’ learning. We then review existing frameworks to identify important components of mathematics assessment tasks. We discuss issues that pertain to the design of assessment tasks and, finally, elaborate on the interpretation of students’ responses and teachers’ actions.

1.2.1. Classroom Assessment

Research suggests that classroom assessment practices for formative purposes have the potential to increase student achievement, and to lead to long-term gains in mathematics performance [ 1 , 4 ]. Particularly, the use of assessment data to individualize instruction has been associated with significant increases in students’ achievement [ 5 ]. It has also been found that the speed of learning can be doubled, and the gap between high and low achievers can be reduced [ 1 , 6 ]. Assessment techniques that are embedded within the classroom instruction have also been shown to support teachers in developing better understanding of students’ thinking and misconceptions [ 7 ].

Classroom assessment for formative purposes consists of eliciting evidence using instruments that are aligned with instruction and the specific domain, identifying patterns in students’ learning, combining the evidence with general principles to provide meaningful feedback, embedding the assessment into the instructional practice, and designing instructional adjustments [ 8 , 9 , 10 , 11 ]. However, less emphasis has been placed on the aspect of instructional adjustments [ 12 ].

Classroom assessment for formative purposes could range from formative assessment lessons [ 13 ] to cognitive diagnostic items [ 14 ]. Formative assessment lessons present a rather integrated ongoing approach of assessment [ 13 ], while cognitive diagnostic items are intended to provide fine-grained analysis of students’ cognitive knowledge [ 15 ]. Classroom assessment practices also include journal reflection, questioning techniques, challenging assignments, assessment tasks, and open-ended performance tasks [ 16 , 17 ]. The various approaches tend to capture students’ learning in order to connect assessment with instruction [ 18 ]. The interpretation could be based on the identification of misconceptions, the categorization of students’ strategies, and the quality of students’ arguments.

Among the various practices for eliciting evidence of students’ current learning, the focus in this paper is on a planned process—that of written assessment tasks. Tasks could provide information about where students stand in terms of learning progression, as well as their levels of understanding [ 19 ]. Mathematics tasks for assessment purposes could be used in everyday mathematics teaching, depending on what was taught and what the teacher intends to assess. Tasks should not necessarily form a test, but independent tasks have the potential to provide chunks of information regarding students’ learning in terms of the teaching and learning processes. Empirical results suggest that, within the context of one unit in primary school, it is possible to employ rather extensive formative assessment practices [ 20 ].

1.2.2. Frameworks for Mathematics Assessment Tasks

We review and analyze frameworks that are relevant to the design and analysis of assessment tasks ( Table 1 ). The first framework, “classroom challenges”, presents four genres of tasks, and was designed to assess and enhance students’ ability to solve multistep, non-routine problems [ 13 ]. The second framework presents three levels of thinking [ 21 ]. The first framework aligns with a rather radical approach to the classroom culture—that of designing whole lessons of formative assessment—while the second seems to focus more on the design and selection of independent tasks. In this paper, our approach to formative assessment aligns more closely with the design of tasks instead of lessons, as we regard this as an intermediary step along the endeavor of integrating formative assessment in school classrooms.

Existing frameworks for assessment tasks.

We also review frameworks of assessment tasks that are widely used—even in large-scale studies, mainly for summative purposes—to identify important components that need to be taken into consideration. We agree with Thompson et al. that “a given assessment task can be either formative or summative, depending on how the information gathered from that task is used” [ 22 ] (p. 4). Harlen also suggests that assessment information could be used “for both summative and formative purposes, without the use for one purpose endangering the effectiveness of use for the other” [ 23 ] (p. 215).

Most of these frameworks, including the two aforementioned ones, seem to place emphasis on important mathematical processes, and on procedural and conceptual aspects of mathematical ideas. The MATH taxonomy is a modification of Bloom’s taxonomy for structuring mathematics assessment tasks, and describes the skills that a particular task assesses [ 24 ]. Bloom et al. developed a taxonomy for the design and assessment of classroom activities that consist of knowledge, comprehension, application, analysis, synthesis, and evaluation [ 25 ]. The TIMSS framework was developed for the purpose of large-scale assessments to compare students’ mathematics achievement in different cognitive domains and content areas, identify trends in students’ performance, and inform evidence-based decisions for improving educational policy and practice across countries over more than 25 years [ 26 ]. The MATH taxonomy, TIMSS framework, and de Lange levels seem to have been influenced by Bloom’s taxonomy. Furthermore, the QCAI framework was designed to assess students’ understanding, reasoning, problem solving, and communication in different content areas in order to measure growth in mathematics over time [ 27 ]. Finally, the SPUR framework suggests that teachers need to assess understanding of the mathematical content that they teach from four dimensions in order to ensure a balanced perspective in teaching and assessment: algorithms and procedures (skills), underlying principles (properties), applications (uses), and diagrams, pictures, or other visual representations (representation) [ 28 ].

The first five frameworks attempt to highlight the nature of mathematics by incorporating important mathematical processes such as problem solving, reasoning and proof, communication, connections, and representation. The last five frameworks refer to the application of procedures or skills in various ways to mathematical concepts or relationships. The second, third, and fourth frameworks more clearly incorporate the idea of assessing students from reproduction to application, and then to mathematical reasoning.

The categorization of tasks in the frameworks above is informative about the kinds of processes that students would need to engage with throughout the assessment tasks. However, the mere categorization into the types of knowledge or processes presents limitations when it comes to how a classroom teacher could be informed about their students’ learning during a series of lessons on a mathematical idea. Assessment for formative purposes is administered according to students’ needs, and is closely associated with the curriculum [ 29 ]. Sociocognitive and sociocultural theories also seem more suitable for classroom assessment—particularly for achieving alignment between the curriculum and the classroom instruction [ 29 ]. Hence, the proposed framework in this paper relies on these existing frameworks, but also attempts to move a step further by making links between the processes and the interpretation of students’ responses. We aimed for a framework that sheds light on students’ emergent, robust, or even fragmented understanding as they engage with mathematical ideas within a classroom community.

1.2.3. Design of Assessment Tasks

The assessment tasks should be meaningful and worthwhile opportunities to learn, as well as being accessible to students [ 30 ]. They should drive classroom learning activities and indicate what kinds of instruction should be encouraged [ 28 , 30 , 31 ]. Tasks that are intended to elicit students’ thinking are usually longer than typical tasks—such as multiple-choice tasks—and take more time to complete, since they engage students with a higher cognitive load [ 31 ]. It is inevitable that different types of tasks provide different types of evidence regarding students’ understanding. Shorter tasks could be used to provide instant feedback to the teacher about students’ understanding, while longer tasks could provide insight into students’ thinking, and opportunities for classroom discussions.

Students’ previous experiences and familiarity with the mathematical idea(s) being assessed could change the expected student processes [ 32 ]. Students tend to solve tasks that share critical properties with textbooks’ tasks by recalling facts and procedures, while they use creative reasoning for those tasks that do not share those critical properties [ 33 ]. The structure, with respect to the level of openness of the task, is another element to be taken into consideration [ 34 ]. Structuring the task into successive parts lowers its intended demand [ 31 ]. The amount and complexity of textual and visual information, such as the use of terminology and complex sentences, increase students’ reading load [ 35 ]. The complexity of the task could also be determined by the number of steps and variables [ 31 ]. Overall, the way the language is used, as well as the forms of the questions in the tasks, relate to how students engage with them [ 34 ].

Another issue is the context in which the tasks are framed. On the one hand, the context could make the task accessible to students, and give them latitude to display what they know [ 30 ]; on the other hand, the context creates challenges in students’ engagement and in the decision making of the task design (e.g., whether the context plays critical role in the mathematization process) [ 21 ]. These design issues also moderate the feedback that the teacher receives based on students’ engagement with the task. However, the way in which this happens is poorly understood [ 6 ].

1.2.4. Interpretation of Students’ Responses and Teachers’ Actions

The analysis of students’ responses in mathematics assessment tasks needs further study in order to lead to meaningful insight that informs teachers about forthcoming instructional adjustments. Pellegrino, Chudowsky, and Glaser mention that “cognition, observation, and interpretation must be explicitly connected and designed as a coordinated whole. If not, the meaningfulness of inferences drawn from the assessment will be compromised” [ 36 ] (p. 2). Indeed, “good teaching decisions are based on high-quality information” [ 37 ] (p. 100).

Analytic rubrics could be used to interpret students’ responses in tasks, which result in identifying elements that should be included in the response [ 37 ]. Another approach is the use of holistic rubrics, in which the overall quality of students’ work is assigned to predetermined categories [ 37 ]. For example, rubrics have been used to support teachers and students to provide feedback for students’ competencies, and to help both understand the competencies required [ 38 ]. Rubrics support the feedback process which, in turn, seems to have a major impact on students’ learning [ 39 ].

Teachers who have a better understanding of the learning goals might design richer learning experiences, be more prepared to provide effective formative feedback, and plan remediation instruction. Teachers’ forthcoming adjustments based on elicited evidence could include immediate modification of instructional decisions, planning instructional activities, diagnosing learning difficulties, placing students into learning sequences, recording for later use, and even eliciting further evidence [ 37 ]. Teachers need to know how to ensure that the inferences made from assessment tasks are of sufficient quality to understand where the learner is along the learning continuum, and to inform decisions about the next instructional steps to be taken [ 40 ].

Instructional actions that are effective in supporting students’ learning of procedures and skills would differ from those that are appropriate for developing students’ understanding and sense-making [ 41 ]. Tasks with a lower level of challenge may help students to engage easily with classroom activities, as may tasks with multiple representations or solving processes [ 42 ]. Moreover, too many challenging tasks in a limited time may demotivate students, even if such tasks promote mathematical reasoning [ 42 ]. The types of tasks, the variation in challenge level, and the timing are issues to be considered when planning instructional adjustments to support the learning of mathematics.

1.2.5. Aims of the Paper

The purpose of this paper is twofold: first, it aims to present a framework, and second, to examine its application for classroom assessment. The framework provides a tool and the relevant language for designing mathematics assessment tasks and analyzing students’ responses to them. The framework is exemplified with students’ actual responses in assessment tasks in order to develop insight into how the framework could be employed to explore students’ learning of the mathematical idea(s) under study. To do so, we sketch students’ profiles, and then use the framework to set the grounds for making hypotheses for further instructional adjustments.

2.1. Proposed Framework

The framework is presented in Table 2 ; it aligns the design of mathematics assessment tasks with the analysis of students’ responses. The first column presents the names of the three types of tasks—reproduction, application, and generation and reflection tasks. In the second column, we refer to the mathematical processes that students are expected to engage with. These processes are partially determined by the contextual familiarity, which is presented in the third column of the table. The contextual familiarity relies on the previous teaching and learning experiences in the classroom, which are known to the classroom teacher. Students’ responses in each type of task are analyzed through a selected competency shown in the fourth column. Then, students’ responses are characterized using the descriptions presented in the fifth column.

Framework for classroom assessment tasks.

2.1.1. Expected Processes

Several of the frameworks presented in Table 1 appear to agree in assessing students from reproduction tasks to higher level thinking tasks. We relied on the categorization of the task processes in these frameworks to define the expected processes for the three types of tasks, and then further refined these processes with reference to the contextual familiarity. Herein, each process is described according to how students are expected to engage with mathematical ideas. Hence, the processes are operationalized with consideration of the previous teaching and learning experiences in the classroom. Mathematical ideas include facts, rules, definitions, and procedures.

In reproduction tasks, students are expected to rely on recalling mathematical ideas. The minimum requirement is reliance on memory, since the contextual familiarity is that students have had extensive practice with these mathematical ideas (e.g., repeating the same definition in classroom, practicing the multiplication tables). Students may respond not only by reproducing, but also by reconstructing mathematical ideas. Such tasks are part of everyday mathematics teaching, and could inform the teacher whether students are able to respond to tasks that they have practiced extensively.

In application tasks, students are expected to apply mathematical ideas. It does not suffice for students to reproduce taught ideas; they need to decide which mathematical ideas to use, and in what way to use them, according to the format of the task. In detail, the variation in the format of the task creates the need to make inferences and adjust the taught mathematical ideas accordingly.

In generation and reflection tasks, students are expected to reflect on mathematical ideas and generate arguments, justifications, strategies, and models. In such a task, “it requires a process of stepping back and reflection on the information being connected” [ 43 ] (p. 5). Students need to decide not only how to adjust the mathematical ideas to the format of the task, but also how to make sense of the structure of mathematics.

Identifying tasks that correspond to these three types of processes relies on the expected formulation of the tasks. For example, a reproduction task for second-grade students might be an application task for first-grade students. An application task might also engage students in reproducing a known algorithm. Hence, we relied on identifying the expected processes by modifying the approach of the “expected formulation of tasks” for the case of assessment tasks. “The expected formulation of a task represents the path the students in a particular classroom community are anticipated to follow if their community engaged with the task in the ways designed in the curricular resource from which the task was derived” [ 44 ] (p. 70). For the case of assessment tasks, the expected formulation of a task relies on the path that students are anticipated to follow based on what preceded in the lesson plan, and the curriculum materials used in the classroom.

2.1.2. Contextual Familiarity

Mathematical knowledge is developed through the personal (mental) and the institutional (contextual) dimensions [ 45 ]. Hence, the assessment needs to be relevant to the context in which the student participates [ 46 ]. We delineate the adaptation of the “expectation formulation” of assessment tasks by focusing on the contextual familiarity, and in particular determining how familiar the format of the task is, as well as the work procedure to complete the task. We relied only on students’ prior experiences in the classroom, which are known to the teacher, and acknowledge the limitation that students have further experiences from prior grades and the home environment. Since the framework also aims to become a tool for classroom teachers, we focused on a rather simple categorization of the format and the work procedure as “familiar” or “unfamiliar”.

The format of the task refers to how the request of the task is presented, and how the information is given. The format could change due to variation in representations, scenarios, the number of steps, or examples of numbers/shapes. The work procedure refers to the steps for completing the task. In reproduction tasks, both the format and the work procedure are expected to be familiar. The familiarity results from extensive opportunities for practice. In application tasks, the format is expected to be unfamiliar, while the work procedure is expected to be familiar. Thus, students need to identify how to use the taught mathematical idea(s) in an unfamiliar format, but afterwards, the procedure to complete the task is expected to be familiar. The unfamiliar format needs to be substantially different, often in a nuanced way, depending on the mathematical idea(s) under study (e.g., relying on students’ common misconceptions). In generation and reflections tasks, both the format and the work procedure are expected to be unfamiliar. Hence, students not only need to interpret and identify what kind of taught mathematical idea is relevant to the task, but they also need to construct a series of steps to reach a conclusion.

2.1.3. Competency

In the context of this study, we defined as a competency per type of task the mechanism that acts as a lens to analyze students’ responses. In mathematics education, there is great consensus that students need to engage in representation, reasoning and proving, communication, problem solving, generalization, making connections, and modelling [ 27 , 47 ]. These are called processes, practices, or competencies [ 48 ], and also appear in the majority of the frameworks presented in Table 1 . However, for the purpose of classroom assessment, we identified constraints in identifying, for example, at which point of the learning continuum a student is at problem solving for a taught mathematical idea (e.g., addition of fractions). Another constraint was that communication and representation, for example, could be seen as media that convey students’ thinking as identified in different types of tasks. Furthermore, we aimed to identify competencies that could be applicable to a range of mathematical topics for primary mathematics, and could also be used for the characterization of students’ responses. The selected competencies for this framework are fluency, flexibility, and reasoning (fourth column in Table 2 ).

For reproduction tasks, the teacher would intend to explore how fluent the student is in recalling taught mathematical ideas, considering their extent of practice and familiarity with the task. For application tasks, the focus is on students’ flexibility, as the teacher would intend to elicit how students’ mathematical ideas are adapted, related, kept coherent, and “freed from specific contexts” [ 43 ] (p. 3) in various task formats. Generation and reflection tasks turn the focus to students’ reasoning. Reasoning is a common term in mathematics education, often having a meaning close to thinking. Here, reasoning is the production of assertions and justified inferences to reach conclusions using, for example, deductive, inductive, and abductive processes [ 49 ].

2.1.4. Characterization of Students’ Responses

Based on the selected competency for each type of task, the framework presents characterizations of students’ responses. The characterization relies on snapshots of aspects of students’ learning being assessed in the assessment tasks ( Table 3 ). The evidence from students’ responses to a reproduction task could indicate developed fluency, developing fluency, or limited fluency. In the same way, the evidence from an application task indicates developed flexibility, developing flexibility, or limited flexibility, while evidence from a generation and reflection task could suggest developed reasoning, developing reasoning, or limited reasoning.

Characterization of students’ responses.

The framework could be viewed horizontally and vertically in a dynamic fashion. Students’ responses could be compared along the continuum in order to identify how students respond to the same tasks (vertical interpretation). Hence, the teacher could decide on how the whole class performs to the processes of different tasks. Students’ responses could also be used to describe their profiles (horizontal interpretation). Hence, the teacher could decide on what instructional adjustments are most appropriate for each student.

2.2. Development of the Framework

The development of the framework started with the analysis of existing frameworks, and the mathematical ideas under study, by examining the mathematical standards in the curriculum, the terminology, the expected representations, and students’ common misconceptions. Students’ familiarity with the tasks was determined by exploring the types of tasks found in textbooks—since teachers and students rely extensively on the unique textbook series used in all state schools in the educational context under study—as well as teachers’ lesson plans when these were available [ 50 ]. We also explored the content quality by looking at whether the content was sufficiently consistent with the current priorities of the field of mathematics education in order for the tasks to be worthwhile [ 51 ]. We also discussed with mathematics education experts what kinds of evidence each assessment task was meant to elicit. Two mathematics educators, who are experienced in the design of tasks for primary mathematics, advised us on the design and analysis of tasks. Then, we turned our attention to the task features and the specification of the tasks by considering issues that pertain to the design of tasks for classroom assessment. Further on, we implemented the assessment tasks and piloted the characterization of students’ responses. We administered 161 tasks to 5 classrooms from grade 4 to grade 6 over the course of a whole school year. The assessment tasks were administered in collaboration with the classroom teachers when the mathematical ideas assessed in the tasks were taught in the respective classrooms. Students solved the tasks independently. We then analyzed students’ responses to explore whether their responses revealed the expected processes [ 51 ]. Herein, we present the final version of the framework, and empirical data from one classroom, to illustrate the application of the framework for classroom assessment.

2.3. Design of Assessment Tasks

We exemplify the framework with assessment tasks on multidigit multiplication, and discuss the analysis of students’ responses. The origin of multiplication is based on repeated addition and the schema of correspondences [ 52 ]; it is a binary operation with two distinctive inputs, and students need to coordinate the multiplicand (number of elements in each set) and the multiplier (number of such sets), along with the procedure to find the product [ 53 ].

Multidigit multiplication includes a series of steps for finding the product, and relies on extending single-digit multiplication [ 54 ]. Students need to achieve two coordinations: the first coordination is between the magnitudes of factors and the magnitudes of products, while the second coordination is between the expanded forms of factors and the distributive property [ 54 ]. Multiplication methods rely on multiplying digits—either manipulating the digits in their expanded form (e.g., 3 in 36 as 3 tens, or 30) or manipulating them as single digits. Particularly, students’ understanding of the distributive property prepares them for finding the product in multidigit multiplication [ 55 ] in fractions and algebra [ 54 ]. The different types of situations that involve multiplication are equal groups, multiplicative comparison, Cartesian product, and rectangular area [ 56 ].

The assessment tasks for multidigit multiplication were designed and selected based on the contextual familiarity. The decisions were based primarily on the examination of textbooks, since the teaching approach depicted in textbooks is anticipated to be the dominant one in classrooms since teachers, in the educational context in this study, rely heavily on textbooks for planning and implementing their lessons [ 50 ]. In fourth-grade textbooks, the lessons begin with how to use single-digit multiplications to find multidigit multiplications in which one of the factors is a multiple of 10, using the commutative and associative properties. Then, attention turns towards strategies for estimating the product. Afterwards, rectangular arrays are used to find the product of two- and three-digit numbers with one-digit numbers. This approach is then linked with the distributive property of multiplication over addition and subtraction. Finally, the lessons probe students to explore different forms of vertical algorithms (e.g., expanded forms and shorter forms), before reaching the standard algorithm. Below, we present four assessment tasks.

The “reproduction task” (RT) is shown in Figure 1 ; it explores whether students could reproduce two different methods to find the product of a two-digit number by one-digit numbers. Both the standard algorithm and the use of the distributive property are expected to have been taught and practiced beforehand in the classroom. Hence, students are anticipated to have extensive familiarity with the format of the task and the work procedure.

Reproduction task.

The first “application task” (AT1) is shown in Figure 2 . The task intends to engage students in comparing mathematical expressions in different forms (e.g., varying the place of addition and multiplication symbols, the place of digits). The first set of expressions intends to explore whether students understand the distributive property, and whether they would consider the expression (5 + 54) × (1 + 54) as equivalent to 6 × 54. The second set of expressions intends to investigate whether students would inappropriately apply the commutative property by ignoring the place value of numbers. Students are asked to explain their rationale in order to provide further insight into their thinking.

Application task 1.

The second “application task” (AT2) is shown in Figure 3 . The task asks students to use the given information (i.e., 34 × 9 = 306) to find the product in the other expressions, where either the multiplier or the multiplicand differs. The task intends to engage students in adjusting the procedure of the distributive property, since they are asked not to analyze one of the factors in tens and units, but to analyze them according to the given information. In the two application tasks, the work procedure is familiar, but the format of the tasks is unfamiliar, since they have to interpret the given information carefully and adapt the known algorithms.

Application task 2.

The “generation and reflection task” (GRT) is shown in Figure 4 . Students are asked to form an argument to justify whether they agree or disagree with the given statement by exploring how the numerical structure of the factors relates to the product. They are expected to reflect on the structure of the numbers, and to find a counterexample. They also need to verbalize their argument. The format of task is unfamiliar, as is the work procedure, since students need to decide how to work in order to justify an answer.

Generation and reflection task.

We present the analysis of students’ responses from one fourth-grade classroom with 21 students in order to exemplify the application of the framework for classroom assessment. We elaborate on the process of analysis, as well as the vertical and horizontal perspectives of the framework.

3.1. Process of Analysis

The analysis of students’ responses followed two stages: (1) one researcher used the characterizations to code the students’ work; (2) the other two researchers independently coded a sample of students’ responses. Any discrepancies were discussed with the whole group of researchers until consensus was reached.

3.2. Vertical Perspective

The vertical perspective of the framework provides an overall picture of the classroom ( Table 4 ). The analysis suggests that the majority of the students have developed fluency in using the procedure for finding the product. However, the class needs to work further on adapting the procedure to different formats, since 16 students showed limited or developing flexibility. The majority of students also showed limited reasoning. Hence, the results suggest that the teaching needs to focus on instructional actions to enhance students’ flexibility and reasoning.

Vertical perspective.

3.3. Horizontal Perspective

We also elaborate on the horizontal perspective of the framework by presenting selected students’ profiles—namely, the profiles of Lina, Manolis, Eleonora, Evita, and Makis ( Figure 5 ). The selection aimed to (1) illustrate all of the different characterizations (presented in Table 4 ) by relying on students’ responses (i.e., developing and developed fluency; limited, developing, and developed flexibility; and limited, developing, and developed reasoning), and (2) reveal different profiles of students according to how they responded across the tasks. For example, Lina showed developing fluency, and limited flexibility and reasoning, while Makis also showed developing fluency, but developing flexibility and developed reasoning. In this way, it is then possible to compare different students’ profiles, and to use the profiles as cases for discussing instructional adjustments.

Students’ profiles.

Lina. Lina used the taught procedures in the RT, but made computational mistakes when using the distributive property of multiplication over addition and subtraction ( Figure 6 ). It was not possible for her to apply the procedure of multiplication in the ATs. Lina mentioned that 6 × 54 was greater than (5 + 54) × (1 + 54), without converting the second expression into a comparable form (e.g., 59 × 55) to the first one. Similarly, Lina did not use the procedure flexibly to compare the expressions 42 × 9 and 49 × 2. In the AT2, Lina applied the distributive property by splitting the number into tens and digits, without adapting the procedure flexibly based on the given product. In the GRT, Lina mentioned that the product of a two-digit number by 2 is a two-digit number. Lina is developing fluency, but limited flexibility and reasoning are evident in these four tasks for the concept of multiplication under study. In total, seven students had the same profile as Lina.

Lina’s responses.

Manolis. Manolis showed a systematic method of work in the RT ( Figure 7 ). In the AT1, he compared the multiplicands in the first set of expressions, while he tried to find the product in the latter set to compare the expressions. He relied more on the taught procedure than on the magnitude of the numbers (i.e., 4 tens times 9 compared to 4 tens times 2), and made computational mistakes. In the AT2, he adjusted the taught procedure to the context of the task by analyzing the multiplicands based on the given information. In the GRT, Manolis agreed with the given statement, and gave an example to justify his answer. He did not explore the whole spectrum of two-digit numbers to refute the statement. Manolis showed developed fluency and flexibility, while his mathematical reasoning was limited.

Manolis’ responses.

Eleonora. Eleonora also used the taught procedure fluently in the RT ( Figure 8 ). In the AT1, she decided that 59 × 55 is bigger than 6 × 54, without finding the product. In the latter set of expressions, Eleonora decided that the change in the place of numbers does not matter, and said that 42 × 9 is greater than 49 × 2. Even though she adapted the procedure flexibly to respond to the AT1, this was not the case in the AT2, in which she found the product by analyzing the number in tens and units, without considering the given information (i.e., students were anticipated to split 11 into 9 + 2). She either did not consider the given statement, or she faced difficulties in extending her current method of using the procedure of distributive property to find the product. In the GRT, Eleonora found that the double of 50 is a three-digit number, thus presenting a counterexample to refute the argument. Hence, Eleonora showed developed fluency and reasoning, and developing flexibility in the four tasks. In total, four students had the same profile as Eleonora.

Eleonora’s responses.

Evita. Evita used the procedure fluently to find the product in the RT ( Figure 9 ). In the AT1, she was looking for the “right place” of the addition and multiplication signs in order to decide whether the expressions are equivalent. She decided that since 2 × 9 = 9 × 2, the expression 42 × 9 must be equal to 49 × 2. In the AT2, she did not consider the given information to find the products, and instead used the procedure she knew (i.e., analyzing the bigger number in tens and units). Her fluency in reproducing the procedure was noticeable, but she did not show any flexibility in adapting the mathematical ideas to other formats. In the GRT, she identified that there is a set of numbers for which this statement would not be true. However, her reasoning was not presented in a coherent manner. Overall, Evita’s responses in the four tasks indicate developed fluency, limited flexibility, and developing reasoning.

Evita’s responses.

Makis. Makis showed developing fluency in the RT due to computational mistakes in the distributive property over subtraction ( Figure 10 ). In the AT1, he decided that 6 × 54 is greater than (5 + 54) × (1 + 54), because he identified a different sign than the expected one. In the latter expression, he seems to have made an estimation for the product. In the AT2, he used the distributive property similarly to the way in which it was used in the RT, without adapting it to the given information. Lastly, in the GRT, he provided a counterexample to refute the statement. Hence, his responses indicate developing fluency and flexibility, and developed reasoning.

Makis’ responses.

4. Discussion

4.1. vertical view of the framework.

Using the framework as a lens to design tasks and interpret students’ responses is intended to give the teacher an overall idea of the level of the class before delving into further analysis of each student’s level of competency. The framework aims to present an approach that is integrated along the continuum of teaching, learning, and assessment. Specifically, during or after the introduction of a new mathematical idea in a mathematics lesson or in a series of lessons, the teacher could use assessment tasks based on the framework to elicit evidence and interpret students’ responses. The interpretation of students’ responses could then guide the preparation and implementation of the next lesson(s). It is not necessary to offer several tasks within each of the three types of task. The number of tasks per type depends on what aspects of the taught mathematical ideas the teacher aims to assess, and in what ways these aspects are entailed in the designed tasks. In this paper, we focus on students’ written work. However, the framework is not incapable of being used during informal observations of students’ work, or during talk in the classroom.

4.2. Horizontal View of the Framework

Central to the framework is the role of the teacher and the previous learning opportunities in classroom. The expected processes (i.e., recall from memory, application, and generation) are framed by the contextual familiarity (i.e., students’ familiarity with the format of the task and the work procedure). A drawback of large-scale assessment is that it misses the qualitative insights on which classroom assessment could rely in order to characterize students’ emergent ideas, and the ways in which students could improve [ 29 ].

The evidence herein from students’ written responses could be viewed from different perspectives and for different purposes. For example, some could focus more on cognitive difficulties, while others focus more on the level of engagement with important mathematical processes (e.g., representing, modelling, connecting). We do not suggest that different perspectives are contradictory—at times they are complementary. To address this concern, the proposed framework presents a selected competency for each type of task, which is aligned with the expected processes and contextual familiarity. The analysis of students’ responses and the language to characterize the responses are aligned with the selected competencies. The characterizations indicate whether the student has reached a satisfying level (e.g., “developed” flexibility), whether the student is still developing the competency (e.g., “developing” flexibility), or whether the response does not provide evidence that the student is developing the competency (e.g., “limited” fluency). The framework is operationalized for the classroom teachers to inform them about students’ learning in a timely manner, in order that they might use the evidence to plan instructional adjustments.

4.3. Instructional Adjustments

The field of classroom assessment should focus more on how to move directly from the evidence about students’ understanding to the description of appropriate teaching actions [ 36 ]. The framework aligns the design of tasks with the analysis of students’ responses in order to set the grounds for developing hypotheses about the respective alignment with instructional adjustments.

Characterizing the level of students’ fluency could suggest possible actions for the classroom teacher. The case of “developing fluency” (Lina and Makis) indicates that further opportunities for practice could be provided in order to attend more to the series of steps, and to precision in calculations. Since students are expected to recall the mathematical idea from memory, opportunities to enhance this recall could be valued. Further study is needed in order to explore how much practice should be provided, and in what intervals. These answers might vary according to the mathematical idea(s) under study. The case of “limited fluency” is rather puzzling. If a student does not reproduce the taught mathematical idea, then student characteristics and teaching approaches should be studied further.

The cases of “developing flexibility” (Manolis and Eleonora) and “limited flexibility” (Evita and Lina) suggest that features of the tasks were not taken into consideration by the students in order to adapt the taught mathematical idea. Hence, timely feedback and focusing on the features of the tasks could enhance their learning [ 42 ]. In addition, the teaching opportunities could be infused with a variety of formats across the mathematical ideas.

For “developing reasoning” (Evita) and “limited reasoning” (Lina and Manolis), a useful approach might be the development of classroom discussions in which students are asked to persuade their classmates about their line of thought. Scholars suggest the use of prompted self-explanation and accountable talk for the learning processes of understanding and sense-making [ 41 ]. Nevertheless, further research is needed in order to provide insight into effective instructional adjustments. We agree that different processes would require different instructional adjustments. It is more likely that using the same examples with different numbers would make students better at reproducing than applying or reasoning.

4.4. Limitations

The framework is a starting point to discuss and elaborate further on the interplay between the design of assessment tasks and the analysis of students’ responses. Statistical analysis from various classroom settings could provide further insight. Additionally, the framework could be used and be adapted to other educational contexts and grade levels. It would be interesting to explore whether the identified processes, the contextual familiarity, the competencies, and the characterization of students’ responses are applicable and meaningful to other content areas. We anticipate that the proposed framework may have much greater validity for primary teachers, since we relied on several topics of primary mathematics for its development. The three types of processes are widely used in mathematics education and beyond. However, further research is needed in order to explore in what ways the three competencies and the characterizations of students’ responses are perceived and applied by the classroom teachers.

Moreover, it would be useful to explore the extent to which the proposed framework might be relevant in settings that use a different textbook than the one on which the framework was developed, or in settings that rely on a varied set of instructional resources rather than a textbook. We relied on a textbook series that is organized per mathematical topic. Hence, an adaptation of the framework would be needed in order to use it alongside a textbook series that is organized per mathematical process. Regarding the use of varied instructional resources, it is anticipated that the adaptation of the “expected formulation of tasks” for assessment tasks would support the application of the framework to such settings. The design of tasks and the interpretation of students’ responses rely extensively on the anticipated path based on what preceded in the classroom context, which determines the contextual familiarity (i.e., task format and work procedure), irrespective of the number of instructional resources used. Furthermore, it would be purposeful to explore the instructional adjustments in real classroom settings based on the hypotheses drawn from the framework, and how these adjustments relate to students’ learning.

5. Conclusions

There is evidence that classroom assessment for formative purposes has the potential to improve students’ learning [ 4 , 7 ]. This is a timely issue that needs to be further explored by relying on empirical evidence and systematic research. However, its effective implementation in classrooms is still in the early stages. In this paper, we move a step forward by presenting a framework that captures the interplay of the design of mathematics assessment tasks and the analysis of students’ responses along the continuum of teaching, learning, and assessment. The proposed framework provides an operational tool for the purpose of classroom assessment; it aims to provoke research that would develop insight into meaningful evidence for enhancing students’ learning of mathematics, and to set the grounds for systematically exploring instructional adjustments.

Author Contributions

Conceptualization: E.D., C.C., D.P.-P.; Methodology: E.D., C.C., D.P.-P.; Analysis: E.D., C.C., D.P.-P.; Writing—Reviewing: E.D., C.C., D.P.-P. All authors have read and agreed to the published version of the manuscript.

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Conflicts of Interest

The authors declare no conflict of interest.

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

• Navigating Higher Dimensions: Mastering Multivariable Calculus Techniques

Multivariable Calculus: Techniques for Solving Problems in Higher Dimensions

Multivariable calculus, an indispensable mathematical discipline, operates as the foundational framework for unraveling and resolving intricate problems within higher dimensions. As we traverse the well-trodden path from the familiar confines of single-variable calculus to the multifaceted landscape of its multivariable counterpart, an entire arsenal of potent analytical tools is unveiled. These tools not only empower us but also broaden our intellectual horizons, allowing for the nuanced analysis and comprehension of phenomena extending into three-dimensional space and beyond. Within the expansive confines of this blog, we embark on an illuminating journey, meticulously dissecting the fundamental concepts, intricate techniques, and far-reaching applications intrinsic to multivariable calculus. This exploration delves deep into the intrinsic richness of this mathematical domain, unraveling its complexities and shedding light on its profound significance across diverse fields of study. From the rudimentary understanding of multivariable functions to the application of advanced theorems in real-world problem-solving, the narrative unravels the layers of abstraction that characterize this branch of mathematics. Whether you require assistance with your Calculus assignment or seek to deepen your understanding and application of multivariable calculus concepts, this blog provides invaluable insights and resources to support your academic journey in mathematics.

Whether deciphering the intricacies of partial derivatives, grappling with the geometric nuances of the gradient vector, or navigating the complexities of vector calculus with line integrals, Green's Theorem, and surface integrals, the reader is led through a comprehensive understanding of the multifaceted nature of multivariable calculus. Moreover, the discussion extends beyond the theoretical realm, addressing the practical applications of these mathematical tools in physics, engineering, and computer science. By illuminating the interplay between mathematical abstraction and real-world phenomena, this blog underscores the integral role played by multivariable calculus in shaping our comprehension of the complex and dynamic systems that govern our universe. As we traverse the vast landscape of multivariable calculus, we not only gain proficiency in mathematical techniques but also cultivate an appreciation for the profound impact of these concepts on our ability to navigate and comprehend the intricacies of the world we inhabit. In essence, this exploration serves as an invitation to unravel the beauty and utility inherent in multivariable calculus, transcending its abstract origins to become an indispensable tool for understanding the complexities that define our multidimensional reality.

Basics of Multivariable Calculus:

In the foundational realm of multivariable calculus, we embark on a journey that transcends the limitations of single-variable calculus, embracing the intricacies of functions operating in higher dimensions. The introduction to multivariable functions lays the groundwork, where each variable contributes to a more nuanced understanding of mathematical relationships. Concepts such as input and output spaces in higher dimensions become essential components of this exploration. As we extend the principles of limits and continuity into multiple variables, we encounter a sophisticated framework that demands a comprehensive grasp of the interplay between these variables. Partial derivatives, a cornerstone of multivariable calculus, emerge as the means to dissect the rate of change of a function concerning individual variables, enabling a nuanced understanding of complex systems. The introduction of the gradient vector adds a geometric perspective, transforming calculus into a tool for optimization and directional analysis. Within this domain, the basics of multivariable calculus form the bedrock upon which subsequent mathematical structures and applications are built, providing a robust foundation for tackling challenges in diverse fields. In the pursuit of higher-dimensional understanding, these fundamental principles serve as a gateway to unlocking the true potential of multivariable calculus, where intricate mathematical machinery begins to reveal its power in unraveling the complexities inherent in our three-dimensional world and beyond.

A. Introduction to Multivariable Functions:

Multivariable calculus lays the foundation for understanding and solving problems in higher dimensions. It introduces us to multivariable functions, defining and representing them within the context of multidimensional spaces, expanding our mathematical toolkit.

• Definition and representation of multivariable functions.
• Understanding the input and output spaces in higher dimensions.

B. Limits and Continuity:

Transitioning from single-variable calculus, multivariable calculus extends the concept of limits to functions with multiple variables. Criteria for continuity in higher dimensions are explored, providing insights into the behavior of functions in complex mathematical spaces.

• Extension of limits to multivariable functions.
• Criteria for continuity in multiple variables.

C. Partial Derivatives:

Multivariable calculus delves into partial derivatives, offering a means to comprehend how a function changes concerning each variable independently. Techniques for computing partial derivatives and their applications are crucial in various mathematical and scientific domains.

• Definition and interpretation of partial derivatives.
• Computing partial derivatives using various methods.

D. The Gradient Vector:

The gradient vector emerges as a pivotal concept, providing both direction and magnitude of the steepest ascent of a function in multivariable calculus. Geometric interpretations, applications in optimization, and insights into directional derivatives showcase the practical utility and significance of the gradient vector in navigating functions in higher dimensions.

• Introduction to the gradient vector and its geometric interpretation.
• Applications in optimization and directional derivatives.

Vector Calculus:

Vector Calculus stands as a pivotal branch within the realm of multivariable calculus, offering a sophisticated framework for understanding and analyzing vector fields, line integrals, and surface integrals. At its core, Vector Calculus delves into the intricacies of vector fields, where each point in a region is associated with a vector. These fields serve as a mathematical representation of physical phenomena such as fluid flow, electromagnetic fields, and gravitational forces. Line integrals, a fundamental concept within this domain, extend the notion of definite integrals to the integration of vector fields along curves. Through parameterization and careful computation, line integrals provide insights into quantities such as work done, circulation, and flux. Green's Theorem, a cornerstone in Vector Calculus, establishes a profound connection between line integrals and double integrals, revealing the relationship between the circulation of a vector field around a curve and the flux through the region enclosed by the curve. Surface integrals further expand the scope, allowing us to integrate vector fields over two-dimensional surfaces, providing valuable information about quantities like mass flow and electric flux. The concepts of divergence and curl add another layer of sophistication, offering tools to analyze the behavior of vector fields in three-dimensional space. Altogether, Vector Calculus equips us with a powerful set of tools to model, analyze, and solve problems in physics, engineering, and other scientific disciplines, emphasizing the interplay between geometry and calculus in higher dimensions.

A. Vector Fields:

Multivariable calculus introduces the concept of vector fields, extending our understanding beyond single-variable functions. Vector fields associate a vector with each point in space, creating a dynamic representation of a system's behavior. Visualization and interpretation of these fields offer valuable insights into various physical phenomena and mathematical models.

• Understanding vector fields in multivariable calculus.
• Visualization and interpretation of vector fields.

B. Line Integrals:

In multivariable calculus, line integrals play a pivotal role in analyzing the cumulative effect of a vector field along a curve. Understanding parametrization and computation techniques is essential. Line integrals find applications in physics, where they quantify work done by a force along a path and have implications in diverse fields such as electromagnetism and fluid dynamics.

• Definition and computation of line integrals.
• Parametrization and evaluation techniques.

C. Green's Theorem:

Green's Theorem establishes a profound connection between line integrals and double integrals over a region in the plane. It provides a tool to convert a circulation around a closed curve into a double integral over the enclosed region and vice versa. The theorem has applications in physics, particularly in fluid dynamics and electromagnetism, showcasing its significance in understanding and solving real-world problems.

• Statement and proof of Green's Theorem.
• Applications in calculating circulation and flux.

D. Surface Integrals:

Extending the concept of line integrals, surface integrals bring multivariable calculus into the realm of three-dimensional space. These integrals quantify the flux of a vector field through a surface. Understanding parameterization and computing surface integrals is crucial, allowing for the analysis of quantities such as electric flux and fluid flow over surfaces, with applications ranging from physics to engineering.

• Extending line integrals to surface integrals.
• Parameterization and computation of surface integrals.

E. Divergence and Curl:

In the study of vector calculus, divergence and curl are fundamental operations applied to vector fields. Divergence measures the rate at which a vector field spreads or converges at a given point, providing insights into the field's behavior. On the other hand, curl captures the rotation or circulation tendency within the vector field. Both concepts find applications in physics, including fluid dynamics and electromagnetism, enhancing our ability to model and understand complex systems in higher dimensions.

• Introduction to divergence and curl of vector fields.
• Physical interpretations and applications.

Multivariable Integration:

In the realm of multivariable calculus, the concept of integration undergoes a profound expansion, encapsulating a variety of techniques and applications. Central to this exploration are double integrals, which extend the principles of integration to functions of two variables. These integrals, defined over a region in the Cartesian plane, become powerful tools for calculating areas, volumes, and averages. The transition to triple integrals takes us into the domain of three-dimensional space, where the volume under a surface or within a region can be precisely computed. Understanding the intricacies of triple integrals involves grasping the nuances of different coordinate systems, such as cylindrical and spherical coordinates, unlocking new perspectives in problem-solving. The applications of multivariable integration reverberate through physics and engineering, where the calculation of mass distributions, electric flux, and fluid flow becomes paramount. Furthermore, delving into the intricacies of changing variables and employing polar or spherical coordinates unveils a versatility in approaching problems, allowing for more elegant and efficient solutions. Multivariable integration is not merely a mathematical exercise but a fundamental tool that permeates various disciplines, providing a systematic way to analyze and comprehend phenomena in higher dimensions. As we navigate the complexities of integrating functions over two and three variables, the profound implications and applications of multivariable integration become increasingly apparent, emphasizing its indispensable role in understanding the intricate relationships within our multidimensional world.

A. Double Integrals:

Double integrals are a fundamental concept in multivariable calculus, extending the notion of integration to functions of two variables over a region in the plane. These integrals involve the summation of infinitesimal areas and find applications in calculating quantities such as mass, volume, and average values. The process of evaluating double integrals includes choosing an appropriate integration order and, in certain cases, converting to polar coordinates for increased simplicity.

• Definition and computation of double integrals.
• Change of variables and polar coordinates.

B. Triple Integrals:

Building upon the concept of double integrals, triple integrals extend the integration process to functions of three variables over a region in space. They are crucial for calculating volumes, masses, and other three-dimensional quantities. The evaluation of triple integrals involves choosing suitable integration orders and coordinate transformations, such as cylindrical or spherical coordinates, to simplify calculations. These integrals play a vital role in modeling and analyzing complex physical systems in fields like physics, engineering, and computer graphics.

• Introduction to triple integrals and their applications.
• Evaluating triple integrals in various coordinate systems.

C. Applications in Physics and Engineering:

Multivariable calculus, particularly double and triple integrals, finds widespread applications in physics and engineering. In physics, these techniques are employed to analyze complex physical systems, calculate moments of inertia, and solve problems related to fluid dynamics. In engineering, multivariable calculus is integral in areas such as structural analysis, heat transfer, and electromagnetism. The ability to model and solve real-world problems using multivariable calculus enhances our understanding and manipulation of the physical world, making it an indispensable tool in various scientific and technological disciplines.

• Utilizing multivariable calculus in mechanics, electromagnetism, and fluid dynamics.
• Real-world examples showcasing the importance of multivariable techniques.

Advanced Topics:

In the realm of advanced topics in multivariable calculus, we encounter profound concepts that deepen our understanding of the interplay between mathematical structures and real-world applications. The Fundamental Theorem of Calculus for Line Integrals stands as a cornerstone, illuminating the connection between antiderivatives and line integrals, offering a unifying perspective on seemingly disparate concepts. Stoke's Theorem and Gauss's Theorem further elevate our comprehension, providing powerful tools for relating surface integrals and triple integrals to fundamental principles in vector calculus. Stoke's Theorem establishes a bridge between circulation and flux, showcasing the intrinsic connection between seemingly unrelated vector fields. On the other hand, Gauss's Theorem extends this harmony to the divergence of vector fields, revealing the interdependence of flux and the behavior of vector fields in three-dimensional space. The applications of these advanced theorems resonate across various scientific disciplines, from modeling fluid dynamics and electromagnetic phenomena to understanding the flow of energy and mass in complex systems. As we delve into these advanced topics, we not only enhance our mathematical prowess but also appreciate the elegance with which multivariable calculus encapsulates the intricate dynamics of higher-dimensional spaces, providing a formidable toolkit for tackling the complexities of the natural world.

A. The Fundamental Theorem of Calculus for Line Integrals:

The Fundamental Theorem of Calculus for Line Integrals plays a pivotal role in vector calculus, establishing a fundamental connection between the integral of a vector field and its potential function. This theorem states that under certain conditions, the line integral of a vector field can be evaluated by computing the difference in the potential function at the endpoints of the path. The theorem provides a powerful tool for simplifying calculations and understanding the relationship between conservative vector fields and their potentials, paving the way for applications in physics, engineering, and various scientific disciplines.

• Statement and proof of the fundamental theorem.
• Implications and applications in vector calculus.

B. Stoke's Theorem and Gauss's Theorem:

Stoke's Theorem and Gauss's Theorem are advanced concepts in multivariable calculus that link the surface and volume integrals of vector fields to the behavior of the vector field itself. Stoke's Theorem relates the circulation of a vector field around a closed curve to the flux of the curl of the vector field over the surface enclosed by the curve. Gauss's Theorem, also known as the Divergence Theorem, establishes a relationship between the flux of a vector field across a closed surface and the divergence of the vector field within the enclosed region. Both theorems are essential tools in solving complex problems in fluid dynamics, electromagnetism, and other applied sciences, providing a deeper understanding of the physical implications of vector calculus in higher dimensions.

• Formulations and proofs of Stoke's and Gauss's theorems.
• Practical applications and connections to real-world problems.

Conclusion:

In conclusion, the intricate tapestry of multivariable calculus weaves together a profound understanding of functions in higher dimensions, vector fields, and the integration of diverse mathematical concepts. The journey from partial derivatives to line integrals, and from double to triple integrals, equips mathematicians, scientists, and engineers with a formidable arsenal of analytical tools. Beyond the theoretical framework, the real-world applications of multivariable calculus resonate across disciplines, impacting fields like physics, where it informs the dynamics of celestial bodies and fluid flows, and engineering, where it plays a pivotal role in optimizing structures and systems. The culmination of the fundamental theorems—Green's, Stoke's, and Gauss's—solidifies the elegance and utility of multivariable calculus, offering profound insights into the interconnectedness of mathematical principles and their applicability in tackling complex problems. As we navigate the expansive realms of higher dimensions, the significance of this mathematical discipline becomes increasingly evident, not only as an intellectual pursuit but as an indispensable tool for unraveling the mysteries of the universe and enhancing our ability to model, understand, and innovate in the world of science and technology. In essence, multivariable calculus stands as a testament to the power of mathematical abstraction and reasoning, providing a robust framework for grappling with the challenges presented by the multidimensional complexities inherent in the fabric of our reality.

Post a comment...

Navigating higher dimensions: mastering multivariable calculus techniques submit your assignment, attached files.