mathematical research papers

Mathematics at MIT is administratively divided into two categories: Pure Mathematics and Applied Mathematics. They comprise the following research areas:

Pure Mathematics

• Algebra & Algebraic Geometry
• Algebraic Topology
• Analysis & PDEs
• Mathematical Logic & Foundations
• Number Theory
• Probability & Statistics
• Representation Theory

Applied Mathematics

In applied mathematics, we look for important connections with other disciplines that may inspire interesting and useful mathematics, and where innovative mathematical reasoning may lead to new insights and applications.

• Combinatorics
• Computational Biology
• Physical Applied Mathematics
• Computational Science & Numerical Analysis
• Theoretical Computer Science
• Mathematics of Data

Help | Advanced Search

arXiv is a free distribution service and an open-access archive for nearly 2.4 million scholarly articles in the fields of physics, mathematics, computer science, quantitative biology, quantitative finance, statistics, electrical engineering and systems science, and economics. Materials on this site are not peer-reviewed by arXiv.

arXiv is a free distribution service and an open-access archive for scholarly articles in the fields of physics, mathematics, computer science, quantitative biology, quantitative finance, statistics, electrical engineering and systems science, and economics. Materials on this site are not peer-reviewed by arXiv.

Stay up to date with what is happening at arXiv on our blog.

Latest news

• Astrophysics ( astro-ph new , recent , search ) Astrophysics of Galaxies ; Cosmology and Nongalactic Astrophysics ; Earth and Planetary Astrophysics ; High Energy Astrophysical Phenomena ; Instrumentation and Methods for Astrophysics ; Solar and Stellar Astrophysics
• Condensed Matter ( cond-mat new , recent , search ) Disordered Systems and Neural Networks ; Materials Science ; Mesoscale and Nanoscale Physics ; Other Condensed Matter ; Quantum Gases ; Soft Condensed Matter ; Statistical Mechanics ; Strongly Correlated Electrons ; Superconductivity
• General Relativity and Quantum Cosmology ( gr-qc new , recent , search )
• High Energy Physics - Experiment ( hep-ex new , recent , search )
• High Energy Physics - Lattice ( hep-lat new , recent , search )
• High Energy Physics - Phenomenology ( hep-ph new , recent , search )
• High Energy Physics - Theory ( hep-th new , recent , search )
• Mathematical Physics ( math-ph new , recent , search )
• Nonlinear Sciences ( nlin new , recent , search ) includes: Adaptation and Self-Organizing Systems ; Cellular Automata and Lattice Gases ; Chaotic Dynamics ; Exactly Solvable and Integrable Systems ; Pattern Formation and Solitons
• Nuclear Experiment ( nucl-ex new , recent , search )
• Nuclear Theory ( nucl-th new , recent , search )
• Physics ( physics new , recent , search ) includes: Accelerator Physics ; Applied Physics ; Atmospheric and Oceanic Physics ; Atomic and Molecular Clusters ; Atomic Physics ; Biological Physics ; Chemical Physics ; Classical Physics ; Computational Physics ; Data Analysis, Statistics and Probability ; Fluid Dynamics ; General Physics ; Geophysics ; History and Philosophy of Physics ; Instrumentation and Detectors ; Medical Physics ; Optics ; Physics and Society ; Physics Education ; Plasma Physics ; Popular Physics ; Space Physics
• Quantum Physics ( quant-ph new , recent , search )

Mathematics

• Mathematics ( math new , recent , search ) includes: (see detailed description ): Algebraic Geometry ; Algebraic Topology ; Analysis of PDEs ; Category Theory ; Classical Analysis and ODEs ; Combinatorics ; Commutative Algebra ; Complex Variables ; Differential Geometry ; Dynamical Systems ; Functional Analysis ; General Mathematics ; General Topology ; Geometric Topology ; Group Theory ; History and Overview ; Information Theory ; K-Theory and Homology ; Logic ; Mathematical Physics ; Metric Geometry ; Number Theory ; Numerical Analysis ; Operator Algebras ; Optimization and Control ; Probability ; Quantum Algebra ; Representation Theory ; Rings and Algebras ; Spectral Theory ; Statistics Theory ; Symplectic Geometry

Computer Science

• Computing Research Repository ( CoRR new , recent , search ) includes: (see detailed description ): Artificial Intelligence ; Computation and Language ; Computational Complexity ; Computational Engineering, Finance, and Science ; Computational Geometry ; Computer Science and Game Theory ; Computer Vision and Pattern Recognition ; Computers and Society ; Cryptography and Security ; Data Structures and Algorithms ; Databases ; Digital Libraries ; Discrete Mathematics ; Distributed, Parallel, and Cluster Computing ; Emerging Technologies ; Formal Languages and Automata Theory ; General Literature ; Graphics ; Hardware Architecture ; Human-Computer Interaction ; Information Retrieval ; Information Theory ; Logic in Computer Science ; Machine Learning ; Mathematical Software ; Multiagent Systems ; Multimedia ; Networking and Internet Architecture ; Neural and Evolutionary Computing ; Numerical Analysis ; Operating Systems ; Other Computer Science ; Performance ; Programming Languages ; Robotics ; Social and Information Networks ; Software Engineering ; Sound ; Symbolic Computation ; Systems and Control

Quantitative Biology

• Quantitative Biology ( q-bio new , recent , search ) includes: (see detailed description ): Biomolecules ; Cell Behavior ; Genomics ; Molecular Networks ; Neurons and Cognition ; Other Quantitative Biology ; Populations and Evolution ; Quantitative Methods ; Subcellular Processes ; Tissues and Organs

Quantitative Finance

• Quantitative Finance ( q-fin new , recent , search ) includes: (see detailed description ): Computational Finance ; Economics ; General Finance ; Mathematical Finance ; Portfolio Management ; Pricing of Securities ; Risk Management ; Statistical Finance ; Trading and Market Microstructure
• Statistics ( stat new , recent , search ) includes: (see detailed description ): Applications ; Computation ; Machine Learning ; Methodology ; Other Statistics ; Statistics Theory

Electrical Engineering and Systems Science

• Electrical Engineering and Systems Science ( eess new , recent , search ) includes: (see detailed description ): Audio and Speech Processing ; Image and Video Processing ; Signal Processing ; Systems and Control
• Economics ( econ new , recent , search ) includes: (see detailed description ): Econometrics ; General Economics ; Theoretical Economics

About arXiv

• General information
• How to Submit to arXiv
• Membership & Giving

Computing the theta function

A quick estimate for the volume of a polyhedron (with m. rudelson), when a system of real quadratic equations has a solution (with m. rudelson), smoothed counting of 0-1 points in polyhedra, testing systems of real quadratic equations for approximate solutions, more on zeros and approximation of the ising partition function (with n. barvinok), a remark on approximating permanents of positive definite matrices, integrating products of quadratic forms, testing for dense subsets in a graph via the partition function (with a. della pella), approximating real-rooted and stable polynomials, with combinatorial applications, stability and complexity of mixed discriminants, computing permanents of complex diagonally dominant matrices and tensors, weighted counting of solutions to sparse systems of equations (with g. regts), approximating permanents and hafnians, concentration of the mixed discriminant of well-conditioned matrices, computing the partition function of a polynomial on the boolean cube, computing the partition function for graph homomorphisms with multiplicities (with p. soberon), computing the partition function for graph homomorphisms (with p. soberon), computing the partition function for cliques in a graph, computing the permanent of (some) complex matrices, on testing hamiltonicity of graphs, convexity of the image of a quadratic map via the relative entropy distance, thrifty approximations of convex bodies by polytopes, approximations of convex bodies by polytopes and by projections of spectrahedra, explicit constructions of centrally symmetric k -neighborly polytopes and large strictly antipodal sets (with s.j. lee and i. novik), a bound for the number of vertices of a polytope with applications, centrally symmetric polytopes with many faces (with s.j. lee and i. novik), neighborliness of the symmetric moment curve (with s.j. lee and i. novik), matrices with prescribed row and column sums, computing the partition function for perfect matchings in a hypergraph (with a. samorodnitsky), the number of graphs and a random graph with a given degree sequence (with j.a. hartigan), an asymptotic formula for the number of non-negative integer matrices with prescribed row and column sums (with j.a. hartigan), maximum entropy gaussian approximation for the number of integer points and volumes of polytopes (with j.a. hartigan), what does a random contingency table look like, on the number of matrices and a random matrix with prescribed row and column sums and 0-1 entries, an approximation algorithm for counting contingency tables (with z. luria, a. samorodnitsky and a. yong), asymptotic estimates for the number of contingency tables, integer flows, and volumes of transportation polytopes, a centrally symmetric version of the cyclic polytope (with i. novik), the computational complexity of convex bodies (with e. veomett), brunn-minkowski inequalities for contingency tables and integer flows, the complexity of generating functions for integer points in polyhedra and beyond, enumerating contingency tables via random permanents, approximating orthogonal matrices by permutation matrices, computing the ehrhart quasi-polynomial of a rational simplex, integration and optimization of multivariate polynomials by restriction onto a random subspace, lattice points, polyhedra, and complexity, convex geometry of orbits (with g. blekherman), c++ codes for estimating permanents, hafnians and the number of forests in a graph, random weighting, asymptotic counting, and inverse isoperimetry (with a. samorodnitsky), short rational generating functions for lattice point problems (with k. woods), estimating l- infinity norms by l 2k norms for functions on orbits, approximating a norm by a polynomial, the distribution of values in the quadratic assignment problem (with t. stephen), the maximum traveling salesman problem (with e.kh. gimadi and a.i. serdyukov), new permanent estimators via non-commutative determinants, a c++ code to compute bounds for the permanent of a 0-1 matrix by the ``average distance'' approach, the distance approach to approximate combinatorial counting (with a. samorodnitsky), a remark on the rank of positive semidefinite matrices subject to affine constraints, polynomial time algorithms to approximate permanents and mixed discriminants within a simply exponential factor, finding maximum length tours under polyhedral norms (with d. johnson, g. woeginger, and r. woodroofe), an algorithmic theory of lattice points in polyhedra (with j. pommersheim).

Publications — Over 100 years of publishing excellence

• Book Author Resources
• Submit a Book Proposal
• AMS Rights, Licensing, and Permissions
• Open Math Notes
• Frequently asked questions
• Member Journals
• Research Journals
• Translation Journals
• Distributed Journals
• Open Access Journals
• Guidelines and Policies

Journal Author Resources

Librarian resources.

• eBook Collections
• COUNTER Usage Statistics
• My Subscriptions
• Subscription Information
• Licensing Information

Mathematical Reviews/MathSciNet®

• MathSciNet ®
• Reviewer Home
• MathSciNet ® Subscriptions

Membership — Welcome to your membership center

Join the ams, renew your membership, give a membership, individual membership.

• Member Benefits
• Member Directory
• Reciprocating Societies
• Members in Developing Countries

Institutional Membership

• Domestic Institutions
• International Institutions
• Two-Year Institutions
• Graduate Student Chapter Program

Other Member Types

• Corporate Memberships
• Associate Memberships

Meetings & Conferences — Engage with colleagues and the latest research

National meetings.

• Joint Mathematics Meetings
• Upcoming JMMs
• Previous JMMs
• Special Lectures
• Professional Enhancement Programs (PEPs)

Sectional Meetings

• Upcoming Sectionals
• Previous Sectionals
• Presenting Papers
• Hosting Sectionals

Other Meetings, Conferences & Workshops

• Mathematics Research Communities
• Education Mini-conference
• International Meetings
• Mathematics Calendar
• Short Courses
• Workshop for Department Chairs and Leaders

Meetings Resources

• Suggest a Speaker
• AMS Meetings Grants
• Submitting Abstracts
• Welcoming Environment Policy
• MathSafe – supporting safe meetings

News & Outreach — Explore news, images, posters, and mathematical essays

News from the ams.

• AMS News Releases
• Feature Stories
• Information for Journalists
• In Memory Of

Math Voices

• Feature Column
• Math in the Media
• Column on Teaching and Learning

Explorations

• Recognizing Diverse Mathematicians
• AMS Posters
• Mathematics & Music
• Mathematical Imagery
• Mathematical Moments

Professional Programs — Resources and opportunities to further your mathematical pursuits

Professional development.

• Employment Services
• Mathjobs.org
• BEGIN Career Initiative
• Mathprograms.org
• Mathematical Opportunities Database
• Research Seminars

Institutional Information and Data

• Annual Survey of the Mathematical and Statistical Sciences
• CBMS Survey
• Other Sources of Data
• Directory of Institutions in the Mathematical Sciences
• Professional Directory

Grants & Support

• AMS-Simons Grants for PUI Faculty
• Travel Grants
• Fellowships & Scholarships
• Epsilon Fund
• Child Care Grants

Awards & Recognition

• AMS Prizes & Awards
• Fellows of the AMS

Education — Resources to support advanced mathematics teaching and learning

For students.

• Information for Undergraduate and High School Students
• Research Experiences for Undergraduates (REUs)
• Considering Grad School
• Find Grad Programs
• Applying to Grad School
• What do Mathematicians Do?

For Teachers

• Teaching Online
• Teaching Resources
• Inclusive Classrooms
• Assessing Student Learning
• Education Webinars

For Department Leaders & Mentors

• Information for Department Leaders
• paraDIGMS (Diversity in Graduate Mathematical Sciences)

Government Relations — Advocating for the mathematical sciences

Elevating mathematics in congress.

• Our Mission
• Letters, Statements, & Legislation
• Congressional Briefings

Legislative Priorities

• Federal Issues of Concern
• Federal Budget Process

Get Involved

• Advocacy Resources
• Take Action

DC-Based Fellowships

• Congressional Fellowship
• Mass Media Fellowship
• Catalyzing Advocacy in Science & Engineering (CASE) Fellowship

Giving to the AMS — Your gifts make great things happen for mathematics   Make a Gift

What you can support.

• The 2020 Fund
• Next Generation Fund
• Birman Fellowship for Women Scholars
• JMM Child Care Grants
• MathSciNet for Developing Countries

Create a Legacy

• Make a Tribute Gift
• Create a Permanent Fund
• Establish a Prize, Award or Fellowship
• Bequests and Charitable Estate Planning

Honoring Your Gift

• Donor Stories
• Donor Wall of Honor
• Thomas S. Fiske Society
• AMS Contributors Society
• AMS Gardens

Giving Resources

• AMS Development Committee
• AMS Gift Acceptance Policy

About the AMS — Advancing research. Connecting the mathematics community.

Our organization.

• Executive Staff
• Equity, Diversity, & Inclusion
• Jobs at AMS
• Customer Service

Our Governance

• Board of Trustees
• Executive Committee

Governance Operations

• Calendar of Meetings
• Policy Statements & Guidelines

On March 21 st , the AMS website will be down for regularly scheduled maintenance from 5:00am–8:00am

Our high quality, peer-reviewed journals have been published since 1891 and cover a broad range of mathematical disciplines. By publishing with the AMS, your book will be part of one of the most respectable collections of mathematical literature in the world. Here, we offer a step-by-step guide to help you publish with the AMS, starting with selecting the right journal for your paper.

The AMS uses Centralized Manuscript Processing for initial submission to our journals.

All articles accepted for publication in AMS Journals are peer reviewed by external reviewers. Editors may reject papers without external review that are not suitable for publication in the journal due to reasons such as subject matter or clear weaknesses in scientific content or presentation style.

Historically, the AMS has had a single-anonymous peer-review process in which the reviewers know who the authors of the manuscript are, but the authors do not have access to the information on who the peer reviewers are. In 2021, the AMS Council voted to transition to a double-anonymous peer review process in which both authors and referees of a given article remain anonymous to each other, and this transition is being rolled out across the research journal portfolio.

Questions about the initial submission process should be directed to [email protected] .

New! AMS journal contributors receive 15% off Charlesworth's specialist language editing and publication support services .

AMS Journal Production Steps

Submit your accepted article.

After your article is accepted for publication in an AMS journal, send the electronic source files (.tex and .eps) for the final accepted version of the manuscript to the AMS using one of the submission options below.

Memoirs is an author-prepared publication. Once formatted for print and on-line publication, articles will be published as is with the addition of AMS-prepared frontmatter and backmatter. Articles are not copyedited; however, a confirmation copy will be sent to authors.

• Submit ACCEPTED articles via the AMS Publication Submission system .
• For security and confidentiality reasons, you must have an AMS Web Account . You will be given an opportunity to create an account as you go through the submission process.

Other Option

• Send files via email to [email protected].
• Include a message indicating the name of the publication in which your article is to appear
• Files larger than 10MB cannot be sent via email. Please contact AMS staff for instructions.

Complete instructions on how to send files are included in the author packages .

How to Effectively Write a Mathematics Research Paper

Mathematics research papers are different from standard academic research papers in important ways, but not so different that they require an entirely separate set of guidelines. Mathematical papers rely heavily on logic and a specific type of language, including symbols and regimented notation. There are two basic structures of mathematical research papers: formal and informal exposition .

Structure and Style

Formal Exposition

The author must start with an outline that develops the logical structure of the paper. Each hypothesis and deduction should flow in an orderly and linear fashion using formal definitions and notation. The author should not repeat a proof or substitute words or phrases that differ from the definitions already established within the paper. The theorem-proof format, definitions, and logic fall under this style.

Informal Exposition

Informal exposition complements the formal exposition by providing the reasoning behind the theorems and proofs. Figures, proofs, equations, and mathematical sentences do not necessarily speak for themselves within a mathematics research paper . Authors will need to demonstrate why their hypotheses and deductions are valid and how they came to prove this. Analogies and examples fall under this style.

Conventions of Mathematics

Clarity is essential for writing an effective mathematics research paper. This means adhering to strong rules of logic, clear definitions, theorems and equations that are physically set apart from the surrounding text, and using math symbols and notation following the conventions of mathematical language. Each area incorporates detailed guidelines to assist the authors.

Related: Do you have questions on language, grammar, or manuscript drafting? Get personalized answers on the FREE Q&A Forum!

Logic is the framework upon which every good mathematics research paper is built. Each theorem or equation must flow logically.

Definitions

In order for the reader to understand the author’s work, definitions for terms and notations used throughout the paper must be set at the beginning of the paper. It is more effective to include this within the Introduction section of the paper rather than having a stand-alone section of definitions.

Theorems and Equations

Theorems and equations should be physically separated from the surrounding text. They will be used as reference points throughout, so they should have a well-defined beginning and end.

Math Symbols and Notations

Math symbols and notations are standardized within the mathematics literature. Deviation from these standards will cause confusion amongst readers. Therefore, the author should adhere to the guidelines for equations, units, and mathematical notation, available from various resources .

Protocols for mathematics writing get very specific – fonts, punctuation, examples, footnotes, sentences, paragraphs, and the title, all have detailed constraints and conventions applied to their usage. The American Mathematical Society is a good resource for additional guidelines.

LaTeX and Wolfram

Mathematical sentences contain equations, figures, and notations that are difficult to typeset using a typical word-processing program. Both LaTeX and Wolfram have expert typesetting capabilities to assist authors in writing.

LaTeX is highly recommended for researchers whose papers constitute mathematical figures and notation. It produces professional-looking documents and authentically represents mathematical language.

Wolfram Language & System Documentation Center’s Mathematica has sophisticated and convenient mathematical typesetting technology that produces professional-looking documents.

The main differences between the two systems are due to cost and accessibility. LaTeX is freely available, whereas Wolfram is not. In addition, any updates in Mathematica will come with an additional charge. LaTeX is an open-source system, but Mathematica is closed-source.

Good Writing and Logical Constructions

Regardless of the document preparation system selected, publication of a mathematics paper is similar to the publication of any academic research in that it requires good writing. Authors must apply a strict, logical construct when writing a mathematics research paper.

There are resources that provide very specific guidelines related to following sections to write and publish a mathematics research paper.

• Concept of a math paper
• Title, acknowledgment, and list of authors
• Introduction
• Body of the work
• Conclusion, appendix, and references
• Publication of a math paper
• Preprint archive
• Choice of the journal, submission
• Publication

The critical elements of a mathematics research paper are good writing and a logical construct that allows the reader to follow a clear path to the author’s conclusions.

Good advice. For me, writing an essay on mathematics was very difficult. I did not have enough time and knowledge to write a quality essay. I worked a lot in the library and read many articles on the Internet. I studied information about essay writing. But I couldn’t finish the essay in full. I had to look for professional writers on the subject of mathematics. He helped me finish a few paragraphs. The work was delivered on time and on an excellent assessment.

Comments are closed.

Enago Academy's Most Popular Articles

• Old Webinars
• Webinar Mobile App

Improving Research Manuscripts Using AI-Powered Insights: Enago reports for effective research communication

Language Quality Importance in Academia AI in Evaluating Language Quality Enago Language Reports Live Demo…

• Reporting Research

Beyond Spellcheck: How copyediting guarantees error-free submission

Submitting a manuscript is a complex and often an emotional experience for researchers. Whether it’s…

How to Find the Right Journal and Fix Your Manuscript Before Submission

Selection of right journal Meets journal standards Plagiarism free manuscripts Rated from reviewer's POV

• Manuscripts & Grants

Research Aims and Objectives: The dynamic duo for successful research

Picture yourself on a road trip without a destination in mind — driving aimlessly, not…

How Academic Editors Can Enhance the Quality of Your Manuscript

Avoiding desk rejection Detecting language errors Conveying your ideas clearly Following technical requirements

Top 4 Guidelines for Health and Clinical Research Report

Top 10 Questions for a Complete Literature Review

Sign-up to read more

Subscribe for free to get unrestricted access to all our resources on research writing and academic publishing including:

• 2000+ blog articles
• 50+ Webinars
• 10+ Expert podcasts
• 50+ Infographics
• 10+ Checklists
• Research Guides

We hate spam too. We promise to protect your privacy and never spam you.

I am looking for Editing/ Proofreading services for my manuscript Tentative date of next journal submission:

As a researcher, what do you consider most when choosing an image manipulation detector?

Journal Content Online

Information & ordering, company contacts.

This website requires Javascript in order to display and function properly. Please enable Javascript in your web browser.

All Journals Home Page

All Journals Contents Online

Aims and Scope

Publication.

Publishing since 1994.

6 issues per year, in January, March, May, July, September and November.

Indexing / Reviewing

Current Contents: Physical, Chemical & Earth Sciences: Clarivate Analytics

MathSciNet: American Mathematical Society

Science Citation Index: Clarivate Analytics

Science Citation Index Expanded: Clarivate Analytics

Scopus: Elsevier

ZentralBlatt MATH: Zentralblatt

Reviewed By

Citation report metrics.

Journal Citation Reports: Clarivate Analytics

Coverage Year: 2022

Total Citations: 2043

Journal Impact Factor: 1.000

5-Year Impact Factor: 0.900

Immediacy Index: 0.300

Eigenfactor: 0.00388

“MATHEMATICAL RESEARCH LETTERS” is a registered trademark of International Press of Boston, Inc.

• Math Careers

Search form

• MAA Centennial
• Spotlight: Archives of American Mathematics
• MAA Officers
• MAA to the Power of New
• Council and Committees
• MAA Code of Conduct
• Policy on Conflict of Interest
• Statement about Conflict of Interest
• Recording or Broadcasting of MAA Events
• Policy for Establishing Endowments and Funds
• Avoiding Implicit Bias
• Copyright Agreement
• Principal Investigator's Manual
• Planned Giving
• The Icosahedron Society
• Our Partners
• Advertise with MAA
• Employment Opportunities
• Staff Directory
• 2022 Impact Report
• In Memoriam
• Membership Categories
• Become a Member
• Membership Renewal
• MERCER Insurance
• MAA Member Directories
• New Member Benefits
• The American Mathematical Monthly
• Mathematics Magazine
• The College Mathematics Journal
• How to Cite
• Communications in Visual Mathematics
• About Convergence
• What's in Convergence?
• Convergence Articles
• Mathematical Treasures
• Portrait Gallery
• Paul R. Halmos Photograph Collection
• Other Images
• Critics Corner
• Problems from Another Time
• Conference Calendar
• Guidelines for Convergence Authors
• Math Horizons
• Submissions to MAA Periodicals
• Guide for Referees
• Scatterplot
• Math Values
• MAA Book Series
• MAA Press (an imprint of the AMS)
• MAA Library Recommendations
• Additional Sources for Math Book Reviews
• About MAA Reviews
• Mathematical Communication
• Information for Libraries
• Author Resources
• MAA MathFest
• Proposal and Abstract Deadlines
• MAA Policies
• Invited Paper Session Proposals
• Contributed Paper Session Proposals
• Panel, Poster, Town Hall, and Workshop Proposals
• Minicourse Proposals
• MAA Section Meetings
• Virtual Programming
• Joint Mathematics Meetings
• Calendar of Events
• MathFest Programs Archive
• MathFest Abstract Archive
• Historical Speakers
• Information for School Administrators
• Information for Students and Parents
• Registration
• Getting Started with the AMC
• AMC Policies
• AMC Administration Policies
• Important AMC Dates
• Competition Locations
• Invitational Competitions
• Putnam Competition Archive
• AMC International
• Curriculum Inspirations
• Sliffe Award
• MAA K-12 Benefits
• Mailing List Requests
• Statistics & Awards
• Submit an NSF Proposal with MAA
• MAA Distinguished Lecture Series
• Common Vision
• CUPM Curriculum Guide
• Instructional Practices Guide
• Möbius MAA Placement Test Suite
• META Math Webinar May 2020
• Progress through Calculus
• Survey and Reports
• "Camp" of Mathematical Queeries
• DMEG Awardees
• National Research Experience for Undergraduates Program (NREUP)
• Neff Outreach Fund Awardees
• Tensor SUMMA Grants
• Tensor Women & Mathematics Grants
• Grantee Highlight Stories
• "Best Practices" Statements
• CoMInDS Summer Workshop 2023
• MAA Travel Grants for Project ACCCESS
• 2024 Summer Workshops
• Minority Serving Institutions Leadership Summit
• Previous Workshops
• Frequently Asked Questions
• Course Resources
• Industrial Math Case Studies
• Participating Faculty
• 2020 PIC Math Student Showcase
• Previous PIC Math Workshops on Data Science
• Dates and Locations
• Past Programs
• Leadership Team
• Support Project NExT
• Section NExT
• Section Officers Meeting History
• Preparations for Section Meetings
• Bylaws Template
• Editor Lectures Program
• MAA Section Lecturer Series
• Officer Election Support
• Section Awards
• Section Liaison Programs
• Section Visitors Program
• Expense Reimbursement
• Guidelines for Bylaw Revisions
• Guidelines for Local Arrangement Chair and/or Committee
• Guidelines for Section Webmasters
• MAA Logo Guidelines
• MAA Section Email Policy
• Section Newsletter Guidelines
• Statement on Federal Tax ID and 501(c)3 Status
• Communication Support
• Guidelines for the Section Secretary and Treasurer
• Legal & Liability Support for Section Officers
• Section Marketing Services
• Section in a Box
• Subventions and Section Finances
• Web Services
• Joining a SIGMAA
• Forming a SIGMAA
• History of SIGMAA
• SIGMAA Officer Handbook
• MAA Connect
• Meetings and Conferences for Students
• Opportunities to Present
• Information and Resources
• MAA Undergraduate Student Poster Session
• Undergraduate Research Resources
• MathFest Student Paper Sessions
• Research Experiences for Undergraduates
• Student Poster Session FAQs
• High School
• A Graduate School Primer
• Reading List
• Student Chapters
• Awards Booklets
• Carl B. Allendoerfer Awards
• Regulations Governing the Association's Award of The Chauvenet Prize
• Trevor Evans Awards
• Paul R. Halmos - Lester R. Ford Awards
• Merten M. Hasse Prize
• George Pólya Awards
• David P. Robbins Prize
• Beckenbach Book Prize
• Euler Book Prize
• Daniel Solow Author’s Award
• Henry L. Alder Award
• Deborah and Franklin Tepper Haimo Award
• Certificate of Merit
• Gung and Hu Distinguished Service
• JPBM Communications Award
• Meritorious Service
• MAA Award for Inclusivity
• T. Christine Stevens Award
• Dolciani Award Guidelines
• Morgan Prize Information
• Selden Award Eligibility and Guidelines for Nomination
• Selden Award Nomination Form
• AMS-MAA-SIAM Gerald and Judith Porter Public Lecture
• Etta Zuber Falconer
• Hedrick Lectures
• James R. C. Leitzel Lecture
• Pólya Lecturer Information
• Putnam Competition Individual and Team Winners
• D. E. Shaw Group AMC 8 Awards & Certificates
• Maryam Mirzakhani AMC 10 A Awards & Certificates
• Two Sigma AMC 10 B Awards & Certificates
• Jane Street AMC 12 A Awards & Certificates
• Akamai AMC 12 B Awards & Certificates
• High School Teachers
• MAA Social Media

You are here

Writing math research papers: a guide for students and instructors.

• From Amazon
• From the MAA Bookstore

temp hardcoded node--book.tpl.php

Robert Gerver

• Table of Contents

Writing Math Research Papers  is primarily a guide for high school students that describes how to write aand present mathematics research papers. But it’s really much more than that: it’s a systematic presentation of a philosophy that writing about math helps many students to understand it, and a practical method to move students from the relatively passive role of someone doing what is assigned to them, to creative thinkers and published writers who contribute to the mathematical literature.

As experienced writers know, the actual writing is not the half of it. William Zinsser once taught a writing class at the New School for Social Research which involved no writing at all: students talked through their ideas in class and through that process discovered the real story which could be written from their tangle of experiences, hopes and dreams. The actual writing was secondary, once they understood how to find the story and organize it.

Gerver, an experienced high school mathematics teacher, takes a similar approach. The primary audience is high school students who want to prepare formal papers or presentations, for contests or for a “math day” at their high school. But the discovery, research and organizational processes involved in writing an original paper, as opposed to rehashing information from a reference book, can help any student learn and understand math, and the experience will be useful even if the paper is never written.

Gerver leads students through a discovery process beginning with examining their own knowledge of mathematics and reviewing the basics of problem solving. The “math annotation” project follows next, in which students organize their class notes for one topic for presentation to their peers, resulting in a product similar to a section of a textbook or handbook, complete with illustrations and the necessary background and review material. Practical advice about finding a topic, developing it by keeping a research journal, and creating a final product, either a research paper or oral presentation, follows.

Writing Math Research Papers  is directed primarily to students, and could be assigned as a supplementary textbook for high school mathematics classes. It will also be useful to teachers who incorporate writing into their classes or who serve as mentors to the math club, and for student teachers in similar situations. An appendix for teachers includes practical advice about helping students through the research and writing process, organizing consultations, and grading the student papers and presentations. Excerpts from student research papers are included as well, and more materials are available from the web site www.keypress.com/wmrp .

Robert Gerver, PhD, is a mathematics instructor at North Shore High School in New York. He received the Presidential Award for Excellence in Mathematical Teaching in 1988 and the Tandy Prize and Chevron Best Practices Award in Education in 1997. He has been publishing mathematics. Dr. Gerver has written eleven mathematics textbooks and numerous articles, and holds two U.S. patents for educational devices.

Sarah Boslaugh, ( [email protected] ) is a Performance Review Analyst for BJC HealthCare and an Adjunct Instructor in the Washington University School of Medicine, both in St. Louis, MO. Her books include An Intermediate Guide to SPSS Programming: Using Syntax for Data Management  (Sage, 2004), Secondary Data Sources for Public Health: A Practical Guide (Cambridge, 2007), and Statistics in a Nutshell (O'Reilly, forthcoming), and she is Editor-in-Chief of The Encyclopedia of Epidemiology (Sage, forthcoming).

• Log in to post comments

Dummy View - NOT TO BE DELETED

MAA Publications

• Periodicals
• MAA History
• Policies and Procedures
• Support MAA
• Member Discount Programs
• Propose a Session
• MathFest Archive
• Putnam Competition
• AMC Resources
• Curriculum Resources
• Outreach Initiatives
• Professional Development
• Communities

Connect with MAA

Mathematical Association of America P: (800) 331-1622 F: (240) 396-5647 Email: [email protected]

Copyright © 2024

• Terms of Use
• Privacy Policy
• Mobile Version

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Int J Mol Sci

Mathematical Modelling in Biomedicine: A Primer for the Curious and the Skeptic

1 Laboratory of Systems Tumor Immunology, Comprehensive Cancer Center Erlangen and Deutsches Zentrum Immuntherapie (DZI), Department of Dermatology, FAU Erlangen-Nürnberg, Universitätsklinikum Erlangen, 91054 Erlangen, Germany; [email protected] (C.L.); [email protected] (X.L.); [email protected] (M.E.)

Christopher Lischer

Momchil nenov.

2 Institute of Mechanics, Bulgarian Academy of Sciences, Acad. G. Bonchev Str., bl. 4, 1113 Sofia, Bulgaria; [email protected] (M.N.); [email protected] (S.N.)

Svetoslav Nikolov

Martin eberhardt, associated data.

In most disciplines of natural sciences and engineering, mathematical and computational modelling are mainstay methods which are usefulness beyond doubt. These disciplines would not have reached today’s level of sophistication without an intensive use of mathematical and computational models together with quantitative data. This approach has not been followed in much of molecular biology and biomedicine, however, where qualitative descriptions are accepted as a satisfactory replacement for mathematical rigor and the use of computational models is seen by many as a fringe practice rather than as a powerful scientific method. This position disregards mathematical thinking as having contributed key discoveries in biology for more than a century, e.g., in the connection between genes, inheritance, and evolution or in the mechanisms of enzymatic catalysis. Here, we discuss the role of computational modelling in the arsenal of modern scientific methods in biomedicine. We list frequent misconceptions about mathematical modelling found among biomedical experimentalists and suggest some good practices that can help bridge the cognitive gap between modelers and experimental researchers in biomedicine. This manuscript was written with two readers in mind. Firstly, it is intended for mathematical modelers with a background in physics, mathematics, or engineering who want to jump into biomedicine. We provide them with ideas to motivate the use of mathematical modelling when discussing with experimental partners. Secondly, this is a text for biomedical researchers intrigued with utilizing mathematical modelling to investigate the pathophysiology of human diseases to improve their diagnostics and treatment.

1. Science: A World of Systems (and Models)

A good portion of science relies on the cascades of models that represent our reality at different spatial and temporal scales. A model is a simplified and often abstract representation of a complex natural system. Models are used in science to help understand, hypothesize about, or simulate the behavior of the natural systems they represent. Since a model is an abstraction of the natural system, it often includes only those elements, interactions, and processes of the system that are required to investigate the hypotheses in question. By exploiting the innate ability of the human brain to work with abstractions, models make highly complex phenomena accessible to study. In this sense, they can be used as a tool to develop hypotheses and to conceive and execute experiments to test those hypotheses. Models also provide an overview of the current knowledge on the natural system in question, facilitating the exchange of up-to-date information between researchers working on the same topic. Moreover, models can be used to simulate aspects of the natural system. A simulation is a rule-based recapitulation of the natural system’s behavior under relevant conditions using the model.

Since the features of a model are tightly linked to the purpose we want to give to it, there are multiple types of models. Models that are common to any branch of science are semantic models ; these consist in verbalization of the natural system’s features and the hypothesis using natural language. This is the type of model that underlies the results and discussion sections in most scientific papers.

More important for our discussion are the “lab bench” models and the “mathematical” models ( Figure 1 ). A lab bench model is a simplified or analogous version of a natural system employed in experiments under controlled conditions. In molecular and cell biology, lab bench models are usually units of life that can be conveniently propagated and studied in experiments to understand a given biological phenomenon. The consensus is that discoveries made via experimentation with the lab bench model provide insights into the behavior of similar phenomena in other organisms, especially humans. This is the case for cell lines, organoids, and mouse or rat strains with given genotypes or phenotypes, which have been used consistently in biomedicine as models for many human diseases.

Science employs different types of models to represent natural systems. Let us suppose that we are interested in investigating the properties and potential vulnerabilities of a melanoma metastasis (here, the “ natural system ”, visualized with MELC microscopy as in Ostalecki et al. 2017 [ 1 ]). One can represent the natural system with a semantic model , that is, the verbalization in natural language of the key compounds and processes as well as the hypotheses about a melanoma micrometastasis. Under some simplifying assumptions, a melanoma metastasis can be studied with lab bench models . For example, if one is interested in the interplay between cancer and immune cells, it is possible to co-culture tumor cells with relevant types of immune cells in vitro, like in Vescovi et al. 2019 [ 2 ]. In most cases, an alternative option is mathematical models , that is, sets of parametric equations that encode the key properties of metastasis and the hypotheses. The mathematical model is the basis for computational simulations to design experiments or to formulate or explore hypotheses like in Santos et al. 2016 [ 3 ].

A mathematical model is a set of parametric equations or other mathematical entities that encode the basic properties of the investigated natural system and that can be used to perform computational simulations. The same way that there are lab bench models with different features and purpose, there are different classes of mathematical models. One can classify them based on their treatment of the system’s dynamics as static models , which describe the system’s state at a point in time; comparative static models , which compare the properties of the system at different points in time; and dynamic models , which follow changes in the system over time. One can also classify models based on the mathematical apparatus they employ or the knowledge they exploit. There are mathematical models grounded in statistics that are used to process, analyze, and impute quantitative data generated in lab bench experiments or obtained from patient samples. All hypothesis tests and estimators of statistical correlation or inference between biological data sets are essentially (bio)statistical models.

However, there are also mathematical models that encode a mechanistic description of the natural system. This means the model equations and variables account for the interactions between the system’s key biological components and can be used for computational simulation of molecular and cellular processes. There are many subclasses of these models. A significant number of them reside in biophysics, developed to allow physically accurate simulations of atomic movement and molecular interactions in biomolecules including protein–protein interactions, DNA folding, or biomembrane dynamics. Other mechanistic models describe biochemical processes that shape cell phenotypes and cell-to-cell interactions. These are inspired by the mathematical models built in chemistry to understand and predict the kinetics of chemical reactions. In any case, just as one cannot elucidate all the mysteries of modern biomedicine with a single experimental technique, say confocal microscopy, a single subclass of mathematical model is not useful for every purpose. Every problem or hypothesis requires a carefully selected mathematical modelling approach.

2. The Scientific Method and the Role of Mathematical Modelling in It

Contemporary science consists in application of the scientific method and careful examination of the results one obtains with it. In the classical view, the scientific method is composed of three steps: observation of a natural phenomenon, elaboration of a hypothesis based on the observation, and design of an adequate experiment to test the hypothesis. If this is the way one would conceive scientific work nowadays, we would be strictly following the approaches employed by Galileo Galilei, Johannes Kepler, and Isaac Newton at the inception of modern science [ 4 ].

However, if you are a 21st century scientist, you are probably implementing a subtle variation of this method, which we will call the Einstein-grade scientific method. Here, the work is not performed in long-term isolation of a scientific ivory tower. Rather, the scientist continuously interacts with a community of peers. We retain the three basic steps mentioned above, but after the experimental test, one (more or less) immediately communicates the results in a booklet-length scientific publication. Early communication allows for your peers to try and reproduce your results. When experimental evidence accumulates and the underlying hypotheses are accepted, they are integrated in the scientific corpus of the field, that is, the set of theories, data, and hypotheses commonly accepted by the majority of researchers. Furthermore, new observations and experiments are continuously cross-checked against the scientific corpus in a way such that the method has an actual cyclic structure.

In the Einstein-grade scientific method, mathematical and computational modelling plays a pivotal role in many different manners ( Figure 2 ). Firstly, today’s “observations” in the majority of fields of natural sciences, including biomedicine, come as quantitative data that have to be processed, assessed, and analyzed with statistical models. In biomedicine, this is especially true in the case of sequencing data for the detection of common patterns in the sequence or the expression of genes in large cohorts of patients, a task impossible without sophisticated statistical and bioinformatics methods [ 5 ]. The features of these special mathematical models have a significant impact on the conclusions one can derive from sequencing data.

Sketch of the Einstein-grade scientific method (grey boxes) and the place that mathematical modelling occupies in it (blue boxes): the photograph of Albert Einstein is modified from the photo “Albert Einstein colorized” by Michael W. Gorth as stored in Wikimedia (CC-BY-SA-4.0, accession date: 10.08.2020; https://commons.wikimedia.org/wiki/File:Albert_Einstein_colourised_portrait.jpg ).

Secondly, computational models can be utilized to derive, ponder on, or substantiate hypotheses. Mathematical modelling has been employed to design validation experiments or to evaluate whether the results of the experiment agree with the expectations derived from the hypothesis and the scientific corpus . Finally, models can be used to achieve a formalized and unambiguous description of a field’s accepted knowledge in which theories, data, and hypotheses are organized and interconnected through equations. A remarkable example of this power is contained in a recent study by Meyer-Hermann and colleagues, in which a comprehensive mathematical model was used to summarize and elaborate around the contemporary knowledge on B-cell differentiation and maturation in germinal centers [ 6 ]. In one sense, Meyer-Hermann’s model is conceptually close to the equations that make up large physical theories, such as electromagnetism. In Supplementary Table S1 , we include and comment on select publications in which the different manners to deploy models are illustrated for biomedicine.

There are a few more issues to mention and discuss about the role of mathematical models in the scientific method. The formal language of a mathematical model enhances precision and clarity compared with natural-language descriptions in the semantic models usually preferred by biomedical experimentalists. Everybody with adequate training can develop an identical understanding of a statement formulated by an equation, for example, v = v max * S /( K M + S ). However, statements made in natural languages can be vague and can provoke misunderstandings. For example, is there a difference between “transcription factor X activates the expression of gene Y” and “transcription factor X promotes the expression of gene Y”?

The Einstein-grade method constitutes a collective endeavor. This means that it is common to find several researchers from different research institutions and locations and even with backgrounds complementing each other completing one cycle of the scientific method. For example, a German theoretical biologist, a sort of mathematical modeler, can publish a hypothesis based on his modelling efforts which will years later pique the interest of an Indonesian molecular biologist to perform experimental validation. Such occurrences are rather common in physics or chemistry, with a world record in some predictions made by Albert Einstein hundreds of years ago that have been experimentally validated only recently (which is why we use the term Einstein-grade here). However, they can also happen in biomedicine: Hodgkin and Huxley established in the first half of the 20th century a long-lasting scientific collaboration to elucidate the biophysical and biochemical mechanisms behind the initiation and propagation of action potential in nerve cell axons, a key phenomenon in understanding the ability of the nervous system to process and store information. The remarkable culmination of this collaboration was the amalgamation of their discoveries into a mathematical model which formalizes, explains, and quantifies the electrical excitability in nerve cells (see their seminal paper in Alan Hodgkin and Andrew Huxley 1952 [ 7 ] and a historical analysis in Schwiening 2012 [ 8 ]). Interestingly, some of the assumptions and simulations in the Hodgkin–Huxley model led Hodgkin’s team to predict already in 1955 that potassium ion channels can be occupied by multiple ions simultaneously. This prediction was confirmed using X-ray crystallography only in 1998, more than 40 years later, in a paradigmatic instance of the Einstein-grade scientific method in neurobiology [ 9 ].

Lastly, the scientific method is nowadays not monolithic and there are multiple variations of the general workflow commented on here [ 10 ]. This plurality of scientific methods may correspond to the different phases of discovery in diverse disciplines, the nature of the problems tackled, or even the styles of thinking belonging to different scientific communities. This notion applies also to mathematical modelling in biology and biomedicine [ 11 ].

3. The Love-and-Hate Relationship of Biology and Mathematics

The story of mathematics and modelling in biology is rather long, which might come as a surprise to many researchers. Biostatistical modelling and analysis have always been a key method in fields like evolutionary biology. In the beginning of the 20th century and right after the rediscovery of the Mendelian inheritance theory, there were many fundamental contributions to biology from statisticians that tried to bridge the gap between Mendelian genetics and Darwin’s theory of evolution. For example, the journal Biometrika [ 12 ] was established as early as 1901 by several founding fathers of modern statistics like Francis Galton and Karl Pearson with the intention of promoting biometrics, that is, the application of statistics to the analysis of biological data. Nowadays, it is difficult to dive into advanced concepts of evolutionary biology and population genetics without an understanding of mathematical modelling [ 13 ]. We also point out the seminal works of K.L. von Bertalanffy, P.A. Weiss, or M.D. Mesarovic in the application of the general systems theory to organisms dating back to the first part of 20th century (see Drack and Wolkenhauer [ 14 ] for detailed discussion).

In parallel to the search for the link between genetics and evolution theory, a new branch of science originating in physical chemistry was created by researchers interested in the dynamics of chemical reactions in living cells. This field became known as biochemistry, and already in 1913, biochemists made use of mathematical modelling to understand the mechanisms behind enzymatic catalysis. The Michaelis–Menten equation, taught in biochemistry courses throughout the world, is the first-ever mathematical model describing the dynamics of a biochemical reaction (see an updated translation of the original paper in Michaelis et al. 2011 [ 15 ]). We find in this field scientists like Jacques Monod and his team, who used mathematical modelling to understand sophisticated features of enzyme activity, such as allosteric regulation (see the seminal contribution in Monod et al. 1965 [ 16 ] and a 50-year retrospective analysis in Changeaux 2012 [ 17 ]). Fascinated by the elegance of these results, for several decades, a myriad of biochemists devoted their efforts to enzymology, that is, elucidation of the mechanisms of reaction, quantification, and modelling of the enzyme catalysis.

If mathematical modelling is necessary to immerse oneself in the connection between genes, phenotypes, and evolution as well as to understand the inner workings of catalytic proteins, how is it that certain modern biomedical researchers are reluctant to incorporate mathematical and theoretical approaches into their work? In the 1970s and 1980s, new experimental techniques were invented allowing the targeted mutation of selected genes [ 18 ]. These techniques became so fundamental in the hunt for the link between genes, proteins, and cellular functions that they led to the inception of modern molecular biology. An experimental approach based on targeted mutation followed by assessment of their effects has dominated the field since then. It is an approach that relies on advanced experimental skills, trial and error, intuition, and small-scale studies, and perhaps, that was what taught several generations of biomedical researchers that mathematics and formalized systems were somehow unnecessary in biology.

However, nowadays, two developments are turning this trend. On the one hand, newly discovered techniques for producing quantitative high-throughput data on whole classes of biomolecules (the omics revolution) required statistical methodologies for processing and analyzing these massive amounts of data. Additionally, mathematical and computational methods are indispensable in finding insights and connections between genes in these data [ 19 ]. This is the rationale behind medical genomics, the field that scans quantitative high-throughput data to find the genetic causation of diseases. On the other hand, there is mounting evidence that proteins and genes in cells do not work in isolation but rather organize into tightly interconnected networks which are often disturbed in pathological conditions [ 20 ]. These networks contain feedback loops, feedforward loops, or network hubs and gene regulatory circuits that can induce nonlinear behavior like homeostasis, self-sustained oscillations, or biostability [ 21 ]. There features, rather than anecdotic, are intrinsic and necessary to many vital cellular processes, e.g., the cell cycle [ 22 ].

The situation in 2020 is peculiar. We are rapidly conjuring biomedicine that necessarily relies more and more on quantitative high-throughput data, advanced statistics, bioinformatics, and computational modelling [ 23 ]. However, a significant fraction of its practitioners have insufficient mathematical and computational skills, probably ones worse than the generation that was initiated into the quantification of enzyme catalysis through kinetic equations and has recently retired. In line with this and to substantiate further discussion, we will now introduce the basics of mathematical modelling of biochemical networks.

4. A Primer on Mechanistic Modelling of Biochemical Systems

There are mathematical and computational models that encode a mechanistic description of the natural system in which equations and variables account for the interactions between the key biological components of the system, for example, signaling proteins and transcription factors. Among them, there is a family of models that are conceived to integrate the topology of biochemical networks and the kinetics of their molecular interactions with their ability to control cell phenotypes. These models are inspired by the models built in chemistry to understand and predict the kinetics of chemical reactions. These mathematical and computational models are formulated, characterized, and utilized following a well-established procedure common to several branches of physics, chemistry, and engineering, which we name here as the modelling workflow . In a nutshell, the workflow includes the following sequential operations ( Figure 3 ):

The modelling workflow in biomedicine: during model derivation, the biological knowledge and hypotheses about the studied system are encoded in a mathematical model. In model calibration, quantitative experimental data are added to characterize the mathematical model and to give values to the model parameters. In model validation, the ability of the model to make predictions is assessed by judging the agreement between new quantitative data and equivalent simulations of the calibrated model. In model analysis, a validated model is used to investigate the system using computer simulations or other tools like stability analysis.

Model derivation: Biomedical information from scientific literature is surveyed to select relevant biomolecules and interactions for the investigated hypothesis. With this information, a graphical depiction of the network of interacting molecules or cells is sketched. Under some formal or heuristic rules, a mathematical model is derived from the network graph. The mathematical model consists of mathematical equations (i.e., ordinary, partial differential, or integrodifferential equations) or other computational entities (i.e., Boolean-logic networks or Petri nets).

Model calibration: To ensure that the model mimics the behavior of the natural system in a given biological scenario, one has to attribute values to free parameters in the model. In some cases, it is possible to discern these from published quantitative data. More often, however, one has to design and perform biological experiments that produce adequate quantitative data. Later, the mathematical model and the quantitative data are integrated using a computational process which assigns optimal values to the model parameters while minimizing the mismatch between experimental observations and corresponding model simulations.

Model validation: The ability of the model to predict the system’s behavior is judged based on the alignment between quantitative data from a different experiment not used for calibration and the corresponding simulations of the calibrated model. A mismatch between data and simulation leads to reformulation of the hypothesis or the model’s structure, which is reflected in a modification of its mathematical equations and a re-iteration of the entire procedure.

Model analysis: A validated model can be used to design and perform predictive simulations, that is, simulations of the system’s behavior under new biological scenarios. This type of simulations has been successfully deployed to detect potential drug targets or to identify biomarkers for diagnosis in cancer and other multifactorial diseases (see Table S1 for selected examples). Furthermore, tools like stability analysis and bifurcation analysis can uncover nonlinear properties of the investigated network, delineating regions in the system’s phase space with distinctive stability or critical values of the model parameters provoking qualitative changes in the system’s behavior. Despite all the power that mathematical models bring to the table, however, it goes without saying that any prediction will require further experimental validation with lab bench models.

5. Frequent Unfounded Criticisms to Mathematical Modelling in Biomedicine

Now, we will list and discuss misconceptions about mathematical modelling in biomedicine which one can hear rather often when talking to experimental researchers in seminars and conferences (see also Table 1 for a summary).

Top misunderstandings on modelling and how to fight them.

5.1. Mathematical Models Cannot Reproduce the Complexity of Biology

When applied to biology in contrast to other natural sciences like physics or chemistry, this statement is a rather elaborate instance of magical thinking. Cells and physicochemical systems are governed by the same thermodynamic laws as any other natural system, laws that have been formulated in mathematical terms. The complexity of stellar systems’ dynamics is at least comparable with that of physiological systems, yet mathematical modelling is the standard tool to postulate hypotheses, to design experiments, and to formulate theories in astrophysics. The dynamics of the Earth’s atmosphere and climate are governed by the same laws of chemical kinetics and reaction-diffusion that apply to biochemical reactions. However, sophisticated mathematical modelling is behind the daily weather forecast or the recommendations of the Intergovernmental Panel on Climate Change. Besides nineteenth-century holistic thinking, there is not a single solid argument to support the notion that mathematical models cannot reproduce the complexity of biochemical and physiological systems.

5.2. Your Model Is Not Physiological. The Real System Is More Complex Than Your Mathematical Model

It may look like a softer version of the previous statement, but here, the emphasis is different. The idea is that modelling may be a valid option, but the current model does not contain sufficient detail to meaningfully represent the physiological context. When inspected more closely, this statement does not actually criticize mathematical modelling in particular but rather the fundamental act of utilizing any sort of model in biology. As we said above, any model, whether mathematical or experimental, is an abstraction that, rather than contemplating every detail of the system, includes the elements, interactions, and processes necessary to investigate the natural system under the hypothesis in question. This implies an intentional attempt at simplification by the researcher that is a shared feature of mathematical models and cell lines, organoids, or mouse models. This criticism can be countered by stating that the model must be as complex as necessary to capture the hypothesis, a notion equally valid for mathematical and lab bench models.

5.3. You Should Employ Data in Your Mathematical Model

A mathematical model in the sense discussed here always relies on quantitative data. As indicated above, model calibration is only possible with experimental data. Thus, a well-formulated mathematical model is based on quantitative data, which makes the above objection moot. Moreover, the interplay between model and quantitative data can come in different flavors. While usually one both calibrates and validates the model with data, one can also forego calibration in favor of analytical tools like stability analysis and can derive qualitative predictions about the system’s dynamics which are accessible to further experimental validation. Bar-or et al. 2000 [ 24 ] is a classic example of the ability of mathematical models to make qualitative predictions about the regulation of gene circuits from data. In the paper, the authors collected and synthesized all the information available at the time about the interplay between the TF p53 and its transcriptional target and repressor Mdm2 to hypothesize a) that they form a negative feedback loop gene circuit and b) that, under DNA damage, the system displayed oscillations in the expression of its components. They derived a qualitative mathematical model based on these hypotheses and found out that the model simulations predicted actual oscillations in p53 and Mdm2 levels in some experimental scenarios. They further validated this model-based prediction utilizing in vitro experiments. Interestingly, this “design principle” associated to oscillating gene circuits with TFs and their targets and repressors has been found in other master regulator TFs also by integrating quantitative data and mathematical modelling (see the case of NFkB in inflammation in Nelson et al. 2004 [ 25 ]).

5.4. Your Predictions Are Not Experimentally Validated

As explained above, once you perform an Einstein-grade version of the scientific method, it is not mandatory that a single paper conveys all the steps of the method. One team of researchers can formulate and investigate a hypothesis with mathematical modelling and simulations, and another team can follow up with validation experiments once technology and effort allow it (see the case of the neuronal action potential above). This is not to say that modelers are generally exempt from the need to validate, though. They should attempt to engage with experimental collaborators to see their own work come to fruition. An important aspect here is to provide ways of facilitating communication between modelers and experimentalists. In this sense, scientific papers on modelling and simulation should be written in a manner that allows the design of experiments to validate their hypotheses and predictions. Ultimately, this requires using common scientific language understandable for both mathematical modelers and experimental researchers.

5.5. I Do Not See the Clinical Relevance of Your Predictions

Very little of the scientific research in biomedicine delivers immediate clinical relevance, be it results obtained via mathematical modelling or through experimentation. However, at the same time, all basic research has an unpredictable long-term potential for enhancing clinical practice. To illustrate its potential, let us analyze a series of results obtained in the context of miRNA regulation and cancer. MicroRNAs exert posttranscriptional repression of selected gene targets [ 26 ] and play a pivotal role in some cell phenotypes subverted in cancer [ 27 ]. Lai et al. [ 28 ] utilized mathematical modelling to investigate the overarching hypothesis that different miRNAs can cooperate in the repression of some of their targets, a prediction that they experimentally validated for miR-572′s and miR-93′s joint repression of CDKNA1, a key cell cycle protein deregulated in cancer. In a continuation of this work, Schmitz et al. [ 29 ] used hybridization and molecular dynamics simulations of the binding of two cooperative miRNAs on their target mRNA to illustrate the general biophysical feasibility of this mechanism and to elucidate how it works at the molecular level. Moreover, they performed a human genome-wide exploration to systematically look for this type of joint miRNA regulation. Based on these results and further computational simulations, they hypothesized that miRNA cooperativity and its modelling can predict drug targets in cancer. They tested the hypothesis in a case study on cooperativity between miR-205-5p and miR-342-3p and its capacity to repress E2F1-mediated chemoresistance in cancer [ 30 ]. Their model-based prediction was confirmed experimentally. Finally, Lai et al. [ 31 ] extended this approach to the whole genome and systematically identified pairs of miRNAs that cooperatively target upregulated genes in metastatic melanoma. In summary, this series of interconnected papers illustrates how mathematical modelling can lead the way from hypothesis formulation and basic research to identifying potential clinical applications.

6. Rules to Build Mathematical Models That Can Be Understood by Experimentalists

To conclude, we elaborate on a few recommendations for biomedical modelers for when they conceive and implement their mathematical models, which hopefully will help bridge the cognitive chasm between them and experimentalists.

6.1. Know Your Problem

A good modeler should become an expert in the biomedical system that they plan to model. This is the best warranty that the structure and the hypotheses behind the mathematical model make sense and are consistent with the current biomedical knowledge. In addition, becoming an expert on the topic will help in choosing the right model assumptions, data, and hypotheses to be tested. Complementary to this, the best models emerge from constant interaction between competent biomodelers and experimental researchers. Remember, though, that collaboration is productive when communication is fluent, and this is only possible when a common language is spoken. In the present, this common language is the one that modelers need to learn when diving into the biology of the system they want to model. We refer again to Meyer-Hermann et al. 2012 [ 6 ] and their ability as modelers to acquire a deep understanding of B-cell biology and how they translated it into their mathematical model. However, we postulate that, in the long-term, biomedical researchers need in turn to rediscover the more precise language that math offers, which will also help them to quickly grasp advances in their own field of interest. There is an in-between methodology that could rekindle the growth of mathematical skills in experimentalists: network biology. In silico reconstruction, visualization, and modelling of intracellular biochemical networks provide a framework for connecting genes and molecules quantitatively to phenotypes and hence understanding the function and dynamics of cellular systems [ 32 ]. The network biology approach relies on mathematical concepts from graph theory, statistics, and mathematical modelling but is yet intuitive enough to allow a fluent discussion between wet- and dry-lab biologists. This has been, for example, advantageously used by yeast biologists to connect their experimentally detected biological interactions with their effect in cell phenotypes.

6.2. Select the Right Type of Mathematical Model, and Select It Early

The features of the mathematical model largely depend on the aim of the study; the scale and structural complexity of the investigated system; and the quantity, quality, and nature of the available experimental data. A model to investigate the nonlinearity associated with a feedback loop circuit has completely different requirements than a model of quantitative drug dosage in humans. This affects in particular the selection of the mathematical framework in which the model is derived and simulated. There is no single best modelling framework for every biomedical system or purpose, and therefore, the choice of model often relies on a trade-off between several requirements. We want to mention here (a) the computational demand and scalability, (b) the nature and necessary amount of calibration data, and (c) the way time and space are handled in the simulations. Sometimes, standard modelling frameworks are not suited for the problem in question and hybrid computational models of different types need to be considered (Chiam et al. 2006 illustrate how this type of hybridization can be done in the context of signaling pathways [ 33 ]; a discussion of this issue in the context of bacterial infection can be found in Cantone et al. 2017 [ 34 ]). When trying to facilitate the communication between modelers and experimentalists, one interesting approach is rule-based modelling. Compared to more math-heavy methods, rule-based modelling allows compact representations of reaction networks with a language-oriented structure; this makes them similar to semantic models and hence closer to the way of thinking of experimentalists (as a case study, see the epidermal growth factor receptor signaling network built in [ 35 ]).

6.3. Build on Preceding Efforts

To start the derivation of a mathematical model totally from scratch makes sense only when there is no alternative. A prudent modeler should reuse, extend, and adapt preexisting models when possible. In some cases, this will not be possible because the available models are based on different experimental conditions, formulated for a different biological scenario, or derived using an unsuitable modelling framework. In these cases, even if the model is found to be partially incompatible, its assessment will help judge the validity and portability of its assumptions and hypotheses in the context of one’s own modelling effort. If the problem lies in the modelling framework, it is sometimes worth translating the model into one’s chosen framework. In the ideal case, the model authors should have uploaded a fully annotated version of their model to a public repository (e.g., Biomodels [ 36 ]), which facilitates the work of incorporating the model into one’s own. Some tools even allow the semiautomatic translation of models from one formalism to another (see for example OdiFy [ 37 ]). As an example of this idea of building on preceding modelling efforts, in Csikász-Nagy 2009, one can find a comprehensive overview of the cascade of increasingly detailed mathematical models constructed since 1991 to understand the regulation of the cell cycle and how mathematical models are based on or have benefitted from the results obtained with previously developed models [ 38 ].

6.4. The Size Does Not Always Matter

There is nowadays a tendency to moon-shoot everything in biomedicine. This has translated also to biomodelling, and some researchers think that the quality of a mathematical model is measured in terms of the number of model variables as well as the required computational power and the complexity of the simulation algorithms. However, quality in modelling is primarily achieved through the biological precision of the assumptions encoded in the model equations. Thus, models can look simple and be small in terms of their number of equations but can actually possess the right features for the purpose of the specific modelling effort. This is somewhat similar to a BIC ballpoint pen. This is the simplest and cheapest ballpoint pen one can buy, but it actually displays a number of easy-to-overlook sophisticated features conceived to optimize its design in economic, ergonomic, and safety terms. One can also formulate BIC-like mathematical models, in which one gives priority to the description of the biological context and hypothesis and its planned utilization rather than to unnecessary size, complexity, or levels of detail ( Figure 4 ).

BIC pen-like mathematical models: prioritizing the purpose of the model instead of its detailedness . BIC pens look like the simplest and cheapest ballpoint pen one can buy, but their apparent simplicity conceals features conceived to optimize them in economic, ergonomic, and safety terms. In Santos and coworkers 2016 [ 3 ], a similar strategy was followed to build a mathematical model accounting for anticancer dendritic cell (DC) vaccination composed of only two ordinary differential equations, far simpler than other published models [ 41 ]. ( A ) Simplicity in design: BIC pens have a characteristically simple hexagonal structure; this apparently naïve choice significantly reduces the material consumption of the pen and minimizes the required space for storage. An important aspect to consider in DC vaccine modelling is the bioavailability of the cells after their injection. There are much elaborated models describing this process [ 42 ], but for our purpose, it was sufficient to model DC bioavailability with a cyclic piecewise linear function that mimics the known overall behavior of injected DCs. ( B ) Mathematics behind design principles: compared to standard circular pens, BIC pens hardly roll on the surface of a table. This feature was explicitly desired when drafting their design. In Santos et al., we wanted a simple enough model that was still able to mimic the interaction between the tumor and both innate and adaptive immunity; to this end, the model contained two nonlinear kinetic rates in a single equation, which are still able to mimic the basics of the interplay between the tumor and the two branches of immunity. ( C ) Ability to solve problems: in the end, simplicity has to be reconciled with effectiveness. The design of a BIC pen, for example, integrates more characteristics like minimizing the risk of suffocation when swallowing the cap. The predictions made in Santos et al. (2016) in terms of which phenotypic features sensitize the tumor to the therapy were aligned with patient data from clinical trials; furthermore, the model predicted alternative phenotypes that promote therapy resistance. The figures about DC vaccine modelling are adapted from Santos et al. 2016 under the conditions of an open access publication (CC BY 4.0). The figures about the BIC pen were inspired by the content of the webpage www.bicworld.com . Fight by doing: A route map to good mathematical modelling in biomedicine.

6.5. Set Your Results in Stone

One should prepare one’s own models in such a way that they can be understood and reused by other researchers, thereby closing the loop inherent to the scientific method. This is a frequently disregarded aspect in many fields in mathematical biomedicine, in which the number of modeler teams can be counted on two hands, and consequently, any model should have a high potential for reuse, adaptation, or integration. A model that is difficult to reproduce or understand by other modelers is guaranteed to collect virtual dust on its publication shelf. Thus, it is advantageous to implement equations and simulations in standard formats [ 39 ]. Further, whenever possible, the models and their supporting experimental data should be uploaded to repositories [ 36 ]. In closing, we emphasize the importance of the careful manual curation and annotation of mathematical models. In line with this, whenever possible, one should give preference to frameworks that allow for fast, simple, and standardized dissemination and model exchange [ 40 ].

7. The Best of Both Worlds—A Final Note on Mathematics, Models, Big Data, and Experimental Biology

The approach based on semantic and lab bench models has been very successful in past decades in describing many fundamental regulatory pathways in molecular biology. However, due to the massive amount of data produced nowadays, we are quickly reaching its limits. This is especially true (and dramatic) in the description of dynamic systems like heterogeneous cell populations, genomic regulation, or multifactorial diseases like cancer, for which this approach is clearly inadequate. There is no semantic solution to properly characterize multi-variable states, events, or diseases.

There is a clear understanding in the wet-lab biology community that advanced high throughput data analysis approaches are an urgent necessity for them, but in the opinion of many wet-lab biologists, data analysis and modelling are often conceived as a mere press of the button on computers that leads to publication-ready figures and plots within minutes. This has led to an entire industry producing “clickable” data analysis and modelling tools that make little demands on the knowledge of the operator. We think that this can lead to many problems, like reproducibility issues or the inability to critically judge the results produced by those tools, especially since most of them use proprietary algorithms. Additionally, the ability to generate an output from a purchased software or analysis suite might not automatically mean that this output is correct or sensible. Hence, an understanding of the underlying data and modelling theory is important and is often neglected in some wet-lab settings.

In the future, we as a community of biomedical researchers should strive to recognize that we need both sides of the coin, giving them equal weight in considerations like funding or time investment. Biology should orient itself towards the other two major natural science disciplines, physics and chemistry, and try to give their students a well-rounded education in mathematical understanding, data analysis, and modelling as well as in computer programming. Until that time, we need to make sure that we find ways to communicate between the two areas in a way that furthers productive collaboration.

Acknowledgments

Some of the misconceptions about modelling come from actual discussions with experimental and clinical researchers at the Department of Dermatology of the FAU Erlangen-Nürnberg, to whom we are grateful for their honest though at times scathing disagreement. Some parts of the text are based on a presentation given by J.V. at the Heidelberger Institut für Theoretische Studien (HITS), and others are from exchanges of ideas within the laboratory of Systems Tumor Immunology. J.V. also thanks Olaf Wolkenhauer (University of Rostock) for 15 years of continuous discussion on the foundations of systems biology.

Supplementary Materials

The following are available online at https://www.mdpi.com/1422-0067/22/2/547/s1 , Table S1: Real cases of mathematical modeling in biomedicine with additional bibliography and further reading.

Author Contributions

Initial draft: J.V.; Figures: J.V.; Final draft: J.V., M.E., C.L., S.N., M.N.; revision of the draft: J.V., X.L. All authors have read and agreed to the published version of the manuscript.

J.V.’s work in mathematical modelling applied to biomedicine has been generously funded over the years by the German Ministry of Education and Research (BMBF) through the initiatives FORSYS [CALSYS-FORSYS 0315264], e:Bio [e:Bio-miRSys 0316175A, e:Bio-MelEVIR 031L0073A], and e:Med [e:Med-CAPSyS 01ZX1304F, e:Med-MelAutim 01ZX1905A] and targeted initiatives in artificial intelligence [KI-VesD, 031L0244A] as well as by the German Research Foundation (DFG) [Ve642/1-1 in SPP1757] and the Bavarian Government [Gaminfection-UKER]. We also acknowledge support by Deutsche Forschungsgemeinschaft and Friedrich-Alexander-Universität Erlangen-Nürnberg within the funding program Open Access Publishing.

Conflicts of Interest

The authors declare no conflict of interest.

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

• {{subColumn.name}}

AIMS Mathematics

• {{newsColumn.name}}
• Share facebook twitter google linkedin

Unraveling multivariable Hermite-Apostol-type Frobenius-Genocchi polynomials via fractional operators

• Mohra Zayed 1 , 
• Shahid Ahmad Wani 2 ,  ,  , 
• Georgia Irina Oros 3 , 
• William Ramírez 4,5 ,  , 
• 1. Mathematics Department, College of Science, King Khalid University, Abha 61413, Saudi Arabia
• 2. Symbiosis Institute of Technology, Symbiosis International (Deemed) University, (SIU), Pune, Maharashtra, India
• 3. Department of Mathematics and Computer Science, Faculty of Informatics and Sciences, University of Oradea, Oradea 410087, Romania
• 4. Section of Mathematics International Telematic University Uninettuno, Rome 00186, Italy
• 5. Department of Natural and Exact Sciences, Universidad de la Costa, Barranquilla 080002, Colombia
• Received: 05 March 2024 Revised: 22 April 2024 Accepted: 30 April 2024 Published: 20 May 2024

MSC : 11T23, 33B10, 33C45, 33E20, 33E30

• Full Text(HTML)
• Download PDF

This study explores the evolution and application of integral transformations, initially rooted in mathematical physics but now widely employed across diverse mathematical disciplines. Integral transformations offer a comprehensive framework comprising recurrence relations, generating expressions, operational formalism, and special functions, enabling the construction and analysis of specialized polynomials. Specifically, the research investigates a novel extended family of Frobenius-Genocchi polynomials of the Hermite-Apostol-type, incorporating multivariable variables defined through fractional operators. It introduces an operational rule for this generalized family, establishes a generating connection, and derives recurring relations. Moreover, the study highlights the practical applications of this generalized family, demonstrating its potential to provide solutions for specific scenarios.

• operational connection ,
• fractional operators ,
• Eulers' integral ,
• multivariable special polynomials ,
• explicit form ,
• applications

Citation: Mohra Zayed, Shahid Ahmad Wani, Georgia Irina Oros, William Ramírez. Unraveling multivariable Hermite-Apostol-type Frobenius-Genocchi polynomials via fractional operators[J]. AIMS Mathematics, 2024, 9(7): 17291-17304. doi: 10.3934/math.2024840

Related Papers:

• This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ -->

Supplements

Access history.

• Corresponding authors: Email: [email protected] , [email protected] , [email protected] , [email protected] ;  Email: [email protected] , [email protected] , [email protected] , [email protected]

Reader Comments

• © 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )

通讯作者: 陈斌, [email protected]

沈阳化工大学材料科学与工程学院 沈阳 110142

Article views( 25 ) PDF downloads( 8 ) Cited by( 0 )

Associated material

Other articles by authors.

• Mohra Zayed
• Shahid Ahmad Wani
• Georgia Irina Oros
• William Ramírez

Related pages

• on Google Scholar
• Email to a friend
• Order reprints

Export File

Journal of Mathematical Biology

The Journal of Mathematical Biology (JOMB) utilizes diverse mathematical disciplines to advance biological understanding. It publishes papers providing new insights through rigorous mathematical analysis or innovative mathematical tools, with a focus on accessibility to biologists.

• Covers cell biology, genetics, ecology, and more
• Welcomes survey and perspective papers
• Encourages proposals for topical collections
• All submissions undergo single-blind peer review
• Final decisions are made by Editors-in-Chief
• Thomas Hillen,
• Anna Marciniak-Czochra

Societies and partnerships

Latest articles

A mathematical model for hiv dynamics with multiple infections: implications for immune escape.

• Yuming Chen

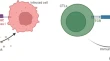
The robustness of phylogenetic diversity indices to extinctions

• Kerry Manson

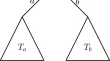
A mathematical model on the propagation of tau pathology in neurodegenerative diseases

• Y. H. Tseng

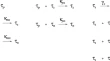
Neuronal activity induces symmetry breaking in neurodegenerative disease spreading

• Christoffer G. Alexandersen
• Alain Goriely
• Christian Bick

Travelling waves for a fast reaction limit of a discrete coagulation–fragmentation model with diffusion and proliferation

• Maxime Estavoyer
• Thomas Lepoutre

Journal updates

The karl-peter hadeler prize winner 2023.

The ESMTB Award Committee unanimously recommend the article titled "Pulled, pushed or failed: the demographic impact of a gene drive can change the nature of its spatial spread" by Lena Kläy, Léo Girardin, Vincent Calvez and Florence Débarre for the Karl-Peter Hadeler prize 2023.

The authors make an important contribution to the analysis of pushed and pulled waves in systems of partial differential equations (PDEs) for genetic drive/wild type invasions. They make new connections between genetic invasions and PDE modelling that allows them to gain relevant ecological insights into observations that result from genetic diversity. The paper is particularly well suited for the K.P. Hadeler prize as K.P. Hadeler himself has published on pulled and pushed invasion waves.

Read and share the article freely using the following link:  https://rdcu.be/dzSn7

The Karl-Peter Hadeler Prize Winner 2022

The ESMTB Award Committee unanimously recommend the article titled "Spatial ecology, optimal control and game theoretical fishing problems" by Idriss Mazari and Domènec Ruiz-Balet for the Karl-Peter Hadeler prize 2022. The mathematical results presented in this article are interesting and well-integrated with the underlying ecological problem, of which they genuinely support a more in-depth theoretical understanding. Both authors are young researchers at an early stage of their academic careers and will thus certainly benefit from being awarded the KPH prize.

Read and share the article freely using the following link:  https://rdcu.be/c5Z46

The Karl-Peter Hadeler Prize

The Karl-Peter Hadeler Prize of the Journal of Mathematical Biology (JoMB) recognizes outstanding publications in the journal.

Call for Papers: Topical Collection on Epidemic Modelling in Honour of Fred Brauer

Fred Brauer, one of the pioneers in mathematical epidemiology, passed away on October 17, 2021, leaving a legacy of exceptional contributions to the field of epidemic modelling including his independent and collaborative research, and his mentorship of multiple generations of researchers in the field.

We are pleased to edit a topical collection for the Journal of Mathematical Biology in his honour. The topical collection covers all areas of epidemiological modelling defined broadly but focuses on using mathematical approaches to gain epidemiological understanding or explain epidemiological phenomena. 

Submission Deadline: 31 October 2022 (Extended)

Guest Editors:  Jianhong Wu, York University; Carlos Castillo-Chavez, Arizona State University; Zhilan Julie Feng, Purdue University; Christopher Kribs, University of Texas at Arlington; Shigui Ruan, University of Miami.

Journal information

• Biological Abstracts
• CAB Abstracts
• Current Contents/Life Sciences
• Google Scholar
• Japanese Science and Technology Agency (JST)
• Mathematical Reviews
• OCLC WorldCat Discovery Service
• Science Citation Index Expanded (SCIE)
• TD Net Discovery Service
• UGC-CARE List (India)
• Zoological Record

Rights and permissions

Editorial policies

© Springer-Verlag GmbH Germany, part of Springer Nature

• Find a journal
• Publish with us
• Track your research

• myState on Mississippi State University
• Directory on Mississippi State University
• Calendars on Mississippi State University
• A-Z Index on Mississippi State University
• Maps on Mississippi State University
• News on Mississippi State University
• Contact on Mississippi State University

Math discovery provides new method to study cell activity, aging, MSU research shows

Contact: Meg Henderson

STARKVILLE, Miss.—New mathematical tools revealing how quickly cell proteins break down are poised to uncover deeper insights into how we age, according to a recently published paper co-authored by a Mississippi State researcher and his colleagues from Harvard Medical School and the University of Cambridge.

Galen Collins, assistant professor in MSU’s Department of Biochemistry, Molecular Biology, Entomology and Plant Pathology, co-authored the groundbreaking paper published in the Proceedings of the National Academy of Sciences, or PNAS, in April.

“We already understand how quickly proteins are made, which can happen in a matter of minutes,” said Collins, who is also a scientist in the Mississippi Agricultural and Forestry Experiment Station. “Until now, we’ve had a very poor understanding of how much time it takes them to break down.”

The paper in applied mathematics, “ Maximum entropy determination of mammalian proteome dynamics ,” presents the new tools that quantify the degradation rates of cell proteins—how quickly they break down—helping us understand how cells grow and die and how we age. Proteins—complex molecules made from various combinations of amino acids—carry the bulk of the workload within a cell, providing its structure, responding to messages from outside the cell and removing waste. 

The results proved that not all proteins degrade at the same pace but instead fall into one of three categories, breaking down over the course of minutes, hours or days. While previous research has examined cell protein breakdown, this study was the first to quantify mathematically the degradation rates of all cell protein molecules, using a technique called maximum entropy.

“For certain kinds of scientific questions, experiments can often reveal infinitely many possible answers; however, they are not all equally plausible,” said lead author Alexander Dear, research fellow in applied mathematics at Harvard University. “The principle of maximum entropy is a mathematical law that shows us how to precisely calculate the plausibility of each answer—its ‘entropy’—so that we can choose the one that is the most likely.”

“This kind of math is sort of like a camera that zooms in on your license plate from far away and figures out what the numbers should be,” Collins said. “Maximum entropy gives us a clear and precise picture of how protein degradation occurs in cells.”

In addition, the team used these tools to study some specific implications of protein degradation for humans and animals. For one, they examined how those rates change as muscles develop and adapt to starvation.

“We found that starvation had the greatest impact on the intermediate group of proteins in muscular cells, which have a half-life of a few hours, causing the breakdown to shift and accelerate,” Collins said. “This discovery could have implications for cancer patients who experience cachexia, or muscle wasting due to the disease and its treatments.”

They also explored how a shift in the breakdown of certain cell proteins contributes to neurodegenerative disease.

“These diseases occur when waste proteins, which usually break down quickly, live longer than they should,” Collins said. “The brain becomes like a teenager’s bedroom, accumulating trash, and when you don’t clean it up, it becomes uninhabitable.”

Dear affirmed the study’s value lies not only in what it revealed about cell protein degeneration, but also in giving scientists a new method to investigate cell activity with precision.

“Our work provides a powerful new experimental method for quantifying protein metabolism in cells,” he said. “Its simplicity and rapidity make it particularly well-suited for studying metabolic changes.”

Collins’s post-doctoral advisor at Harvard and a co-author of the article, the late Alfred Goldberg, was a pioneer in studying the life and death of proteins. Collins noted this study was built on nearly five decades of Goldberg’s research and his late-career collaboration with mathematicians from the University of Cambridge. After coming to MSU a year ago, Collins continued collaborating with his colleagues to complete the paper.

“It’s an incredible honor to be published in PNAS, but it was also a lot of fun being part of this team,” Collins said. “And it’s very meaningful to see my former mentor’s body of work wrapped up and published.”

Since 1914, PNAS has been one of the most authoritative publications of high-impact research in the biological, physical and social sciences. More information and past issues can be found at www.pnas.org . The Mississippi Agricultural and Forestry Experiment Station conducts research that improves human health and well-being. Learn more at www.mafes.msstate.edu .  

Mississippi State University is taking care of what matters. Learn more at  www.msstate.edu .

Monday, May 20, 2024 - 2:58 pm

• Health & Environment News
• Research & Innovation News
• Science & Technology News
• College of Agriculture and Life Sciences

You may also be interested in…

Sound of cicadas: rare insect emergence brings buzz ‘unlike any in nature’.

May 08, 2024

‘Catharsis’ exhibition showcases thesis work of MSU fine arts grads

May 03, 2024

MSU to honor national alumnus Wilson, other alumni this Friday

May 16, 2024

• Find Mississippi State University on Facebook
• Find Mississippi State University on Instagram
• Find Mississippi State University on LinkedIn
• Find Mississippi State University on Pinterest
• Find Mississippi State University on Twitter
• Find Mississippi State University on YouTube

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• 14 May 2024

Why mathematics is set to be revolutionized by AI

• Thomas Fink 0

Thomas Fink is the director of the London Institute for Mathematical Sciences, UK.

You can also search for this author in PubMed   Google Scholar

You have full access to this article via your institution.

Giving birth to a conjecture — a proposition that is suspected to be true, but needs definitive proof — can feel to a mathematician like a moment of divine inspiration. Mathematical conjectures are not merely educated guesses. Formulating them requires a combination of genius, intuition and experience. Even a mathematician can struggle to explain their own discovery process. Yet, counter-intuitively, I think that this is the realm in which machine intelligence will initially be most transformative.

In 2017, researchers at the London Institute for Mathematical Sciences, of which I am director, began applying machine learning to mathematical data as a hobby. During the COVID-19 pandemic, they discovered that simple artificial intelligence (AI) classifiers can predict an elliptic curve’s rank 1 — a measure of its complexity. Elliptic curves are fundamental to number theory, and understanding their underlying statistics is a crucial step towards solving one of the seven Millennium Problems, which are selected by the Clay Mathematics Institute in Providence, Rhode Island, and carry a prize of US$1 million each. Few expected AI to make a dent in this high-stakes arena.

AI now beats humans at basic tasks — new benchmarks are needed, says major report

AI has made inroads in other areas, too. A few years ago, a computer program called the Ramanujan Machine produced new formulae for fundamental constants 2 , such as π and e . It did so by exhaustively searching through families of continued fractions — a fraction whose denominator is a number plus a fraction whose denominator is also a number plus a fraction and so on. Some of these conjectures have since been proved, whereas others remain open problems.

Another example pertains to knot theory, a branch of topology in which a hypothetical piece of string is tangled up before the ends are glued together. Researchers at Google DeepMind, based in London, trained a neural network on data for many different knots and discovered an unexpected relationship between their algebraic and geometric structures 3 .

How has AI made a difference in areas of mathematics in which human creativity was thought to be essential?

First, there are no coincidences in maths. In real-world experiments, false negatives and false positives abound. But in maths, a single counterexample leaves a conjecture dead in the water. For example, the Pólya conjecture states that most integers below any given integer have an odd number of prime factors. But in 1960, it was found that the conjecture does not hold for the number 906,180,359. In one fell swoop, the conjecture was falsified.

Second, mathematical data — on which AI can be trained — are cheap. Primes, knots and many other types of mathematical object are abundant. The On-Line Encyclopedia of Integer Sequences (OEIS) contains almost 375,000 sequences — from the familiar Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, ...) to the formidable Busy Beaver sequence (0, 1, 4, 6, 13, …), which grows faster than any computable function. Scientists are already using machine-learning tools to search the OEIS database to find unanticipated relationships.

DeepMind AI outdoes human mathematicians on unsolved problem

AI can help us to spot patterns and form conjectures. But not all conjectures are created equal. They also need to advance our understanding of mathematics. In his 1940 essay A Mathematician’s Apology , G. H. Hardy explains that a good theorem “should be one which is a constituent in many mathematical constructs, which is used in the proof of theorems of many different kinds”. In other words, the best theorems increase the likelihood of discovering new theorems. Conjectures that help us to reach new mathematical frontiers are better than those that yield fewer insights. But distinguishing between them requires an intuition for how the field itself will evolve. This grasp of the broader context will remain out of AI’s reach for a long time — so the technology will struggle to spot important conjectures.

But despite the caveats, there are many upsides to wider adoption of AI tools in the maths community. AI can provide a decisive edge and open up new avenues for research.

Mainstream mathematics journals should also publish more conjectures. Some of the most significant problems in maths — such as Fermat’s Last Theorem, the Riemann hypothesis, Hilbert’s 23 problems and Ramanujan’s many identities — and countless less-famous conjectures have shaped the course of the field. Conjectures speed up research by pointing us in the right direction. Journal articles about conjectures, backed up by data or heuristic arguments, will accelerate discovery.

Last year, researchers at Google DeepMind predicted 2.2 million new crystal structures 4 . But it remains to be seen how many of these potential new materials are stable, can be synthesized and have practical applications. For now, this is largely a task for human researchers, who have a grasp of the broad context of materials science.

Similarly, the imagination and intuition of mathematicians will be required to make sense of the output of AI tools. Thus, AI will act only as a catalyst of human ingenuity, rather than a substitute for it.

Nature 629 , 505 (2024)

doi: https://doi.org/10.1038/d41586-024-01413-w

He, Y.-H., Lee, K.-H., Oliver, T. & Pozdnyakov, A. Preprint at arXiv https://doi.org/10.48550/arXiv.2204.10140 (2024).

Raayoni, G. et al. Nature 590 , 67–73 (2021).

Article   PubMed   Google Scholar  

Davies, A. et al. Nature 600 , 70–74 (2021).

Merchant, A. et al. Nature 624 , 80–85 (2023).

Download references

Reprints and permissions

Competing Interests

The author declares no competing interests.

Related Articles

• Machine learning
• Mathematics and computing

DeepLabCut: the motion-tracking tool that went viral

Technology Feature 20 MAY 24

How does ChatGPT ‘think’? Psychology and neuroscience crack open AI large language models

News Feature 14 MAY 24

The US Congress is taking on AI — this computer scientist is helping

News Q&A 09 MAY 24

The dream of electronic newspapers becomes a reality — in 1974

News & Views 07 MAY 24

3D genomic mapping reveals multifocality of human pancreatic precancers

Article 01 MAY 24

AI’s keen diagnostic eye

Outlook 18 APR 24

Vice President, Nature Communications Portfolio

This is an exciting opportunity to play a key leadership role in the market-leading journal Nature Portfolio and help drive its overall contribution.

New York City, New York (US), Berlin, or Heidelberg

Springer Nature Ltd

Senior Postdoctoral Research Fellow

Senior Postdoctoral Research Fellow required to lead exciting projects in Cancer Cell Cycle Biology and Cancer Epigenetics.

Melbourne University, Melbourne (AU)

University of Melbourne & Peter MacCallum Cancer Centre

Overseas Talent, Embarking on a New Journey Together at Tianjin University

We cordially invite outstanding young individuals from overseas to apply for the Excellent Young Scientists Fund Program (Overseas).

Tianjin, China

Tianjin University (TJU)

Chair Professor Positions in the School of Pharmaceutical Science and Technology

SPST seeks top Faculty scholars in Pharmaceutical Sciences.

Chair Professor Positions in the School of Precision Instruments and Optoelectronic Engineering

We are committed to accomplishing the mission of achieving a world-top-class engineering school.

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Doctoral students in Mathematics Education and Teacher Education and Teacher Development present at national conference

Posted in: Faculty and Student Research , Presentations , Students and Alumni

John O’Meara, PhD student in Mathematics Education, presented a paper with Shanna Anderson, PhD student in Teacher Education and Teacher Development (TETD), at the National Association of Research in Science Teaching (NARST) conference in Denver, CO on March 19, 2024. They presented their work on Social Network Maps: Supporting STEM Teacher Leaders and Characterizing the Phenomenon of Teacher Leadership, funded by the Wipro Science Education Fellowship grant.

They represented their research team, which includes Drs. Mika Munakata , Emily Klein and Monica Taylor (College of Education and Engaged Learning) and Tim Aberle (PhD student in TETD). Congratulations, all!

• Share full article

Advertisement

Supported by

Study Suggests Genetics as a Cause, Not Just a Risk, for Some Alzheimer’s

People with two copies of the gene variant APOE4 are almost certain to get Alzheimer’s, say researchers, who proposed a framework under which such patients could be diagnosed years before symptoms.

By Pam Belluck

Scientists are proposing a new way of understanding the genetics of Alzheimer’s that would mean that up to a fifth of patients would be considered to have a genetically caused form of the disease.

Currently, the vast majority of Alzheimer’s cases do not have a clearly identified cause. The new designation, proposed in a study published Monday, could broaden the scope of efforts to develop treatments, including gene therapy, and affect the design of clinical trials.

It could also mean that hundreds of thousands of people in the United States alone could, if they chose, receive a diagnosis of Alzheimer’s before developing any symptoms of cognitive decline, although there currently are no treatments for people at that stage.

The new classification would make this type of Alzheimer’s one of the most common genetic disorders in the world, medical experts said.

“This reconceptualization that we’re proposing affects not a small minority of people,” said Dr. Juan Fortea, an author of the study and the director of the Sant Pau Memory Unit in Barcelona, Spain. “Sometimes we say that we don’t know the cause of Alzheimer’s disease,” but, he said, this would mean that about 15 to 20 percent of cases “can be tracked back to a cause, and the cause is in the genes.”

The idea involves a gene variant called APOE4. Scientists have long known that inheriting one copy of the variant increases the risk of developing Alzheimer’s, and that people with two copies, inherited from each parent, have vastly increased risk.

The new study , published in the journal Nature Medicine, analyzed data from over 500 people with two copies of APOE4, a significantly larger pool than in previous studies. The researchers found that almost all of those patients developed the biological pathology of Alzheimer’s, and the authors say that two copies of APOE4 should now be considered a cause of Alzheimer’s — not simply a risk factor.

The patients also developed Alzheimer’s pathology relatively young, the study found. By age 55, over 95 percent had biological markers associated with the disease. By 65, almost all had abnormal levels of a protein called amyloid that forms plaques in the brain, a hallmark of Alzheimer’s. And many started developing symptoms of cognitive decline at age 65, younger than most people without the APOE4 variant.

“The critical thing is that these individuals are often symptomatic 10 years earlier than other forms of Alzheimer’s disease,” said Dr. Reisa Sperling, a neurologist at Mass General Brigham in Boston and an author of the study.

She added, “By the time they are picked up and clinically diagnosed, because they’re often younger, they have more pathology.”

People with two copies, known as APOE4 homozygotes, make up 2 to 3 percent of the general population, but are an estimated 15 to 20 percent of people with Alzheimer’s dementia, experts said. People with one copy make up about 15 to 25 percent of the general population, and about 50 percent of Alzheimer’s dementia patients.

The most common variant is called APOE3, which seems to have a neutral effect on Alzheimer’s risk. About 75 percent of the general population has one copy of APOE3, and more than half of the general population has two copies.

Alzheimer’s experts not involved in the study said classifying the two-copy condition as genetically determined Alzheimer’s could have significant implications, including encouraging drug development beyond the field’s recent major focus on treatments that target and reduce amyloid.

Dr. Samuel Gandy, an Alzheimer’s researcher at Mount Sinai in New York, who was not involved in the study, said that patients with two copies of APOE4 faced much higher safety risks from anti-amyloid drugs.

When the Food and Drug Administration approved the anti-amyloid drug Leqembi last year, it required a black-box warning on the label saying that the medication can cause “serious and life-threatening events” such as swelling and bleeding in the brain, especially for people with two copies of APOE4. Some treatment centers decided not to offer Leqembi, an intravenous infusion, to such patients.

Dr. Gandy and other experts said that classifying these patients as having a distinct genetic form of Alzheimer’s would galvanize interest in developing drugs that are safe and effective for them and add urgency to current efforts to prevent cognitive decline in people who do not yet have symptoms.

“Rather than say we have nothing for you, let’s look for a trial,” Dr. Gandy said, adding that such patients should be included in trials at younger ages, given how early their pathology starts.

Besides trying to develop drugs, some researchers are exploring gene editing to transform APOE4 into a variant called APOE2, which appears to protect against Alzheimer’s. Another gene-therapy approach being studied involves injecting APOE2 into patients’ brains.

The new study had some limitations, including a lack of diversity that might make the findings less generalizable. Most patients in the study had European ancestry. While two copies of APOE4 also greatly increase Alzheimer’s risk in other ethnicities, the risk levels differ, said Dr. Michael Greicius, a neurologist at Stanford University School of Medicine who was not involved in the research.

“One important argument against their interpretation is that the risk of Alzheimer’s disease in APOE4 homozygotes varies substantially across different genetic ancestries,” said Dr. Greicius, who cowrote a study that found that white people with two copies of APOE4 had 13 times the risk of white people with two copies of APOE3, while Black people with two copies of APOE4 had 6.5 times the risk of Black people with two copies of APOE3.

“This has critical implications when counseling patients about their ancestry-informed genetic risk for Alzheimer’s disease,” he said, “and it also speaks to some yet-to-be-discovered genetics and biology that presumably drive this massive difference in risk.”

Under the current genetic understanding of Alzheimer’s, less than 2 percent of cases are considered genetically caused. Some of those patients inherited a mutation in one of three genes and can develop symptoms as early as their 30s or 40s. Others are people with Down syndrome, who have three copies of a chromosome containing a protein that often leads to what is called Down syndrome-associated Alzheimer’s disease .

Dr. Sperling said the genetic alterations in those cases are believed to fuel buildup of amyloid, while APOE4 is believed to interfere with clearing amyloid buildup.

Under the researchers’ proposal, having one copy of APOE4 would continue to be considered a risk factor, not enough to cause Alzheimer’s, Dr. Fortea said. It is unusual for diseases to follow that genetic pattern, called “semidominance,” with two copies of a variant causing the disease, but one copy only increasing risk, experts said.

The new recommendation will prompt questions about whether people should get tested to determine if they have the APOE4 variant.

Dr. Greicius said that until there were treatments for people with two copies of APOE4 or trials of therapies to prevent them from developing dementia, “My recommendation is if you don’t have symptoms, you should definitely not figure out your APOE status.”

He added, “It will only cause grief at this point.”

Finding ways to help these patients cannot come soon enough, Dr. Sperling said, adding, “These individuals are desperate, they’ve seen it in both of their parents often and really need therapies.”

Pam Belluck is a health and science reporter, covering a range of subjects, including reproductive health, long Covid, brain science, neurological disorders, mental health and genetics. More about Pam Belluck

The Fight Against Alzheimer’s Disease

Alzheimer’s is the most common form of dementia, but much remains unknown about this daunting disease..

How is Alzheimer’s diagnosed? What causes Alzheimer’s? We answered some common questions .

A study suggests that genetics can be a cause of Alzheimer’s , not just a risk, raising the prospect of diagnosis years before symptoms appear.

Determining whether someone has Alzheimer’s usually requires an extended diagnostic process . But new criteria could lead to a diagnosis on the basis of a simple blood test .

The F.D.A. has given full approval to the Alzheimer’s drug Leqembi. Here is what to know about i t.

Alzheimer’s can make communicating difficult. We asked experts for tips on how to talk to someone with the disease .